[APIO2010]巡逻（树的直径）

[APIO2010]巡逻

题目描述

在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。 下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的 圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距 离为 14 个单位，每条道路都需要经过两次。

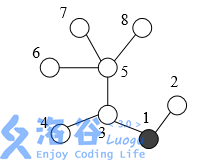
为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路， 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 （见下面的图例（c））。 一条新道路甚至可以是一个环，即，其两端连接到同一 个村庄。 由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子：

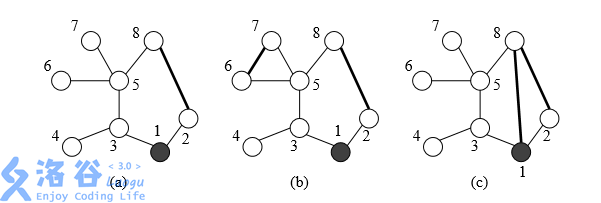
在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总 的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路 正好一次，总的距离变为了 15。 试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳 的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

输入输出格式

输入格式：

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b， 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

输出格式：

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

输入输出样例

输入样例#1： 复制

8 1

1 2

3 1

3 4

5 3

7 5

8 5

5 6

输出样例#1： 复制

11

输入样例#2： 复制

8 2

1 2

3 1

3 4

5 3

7 5

8 5

5 6

输出样例#2： 复制

10

输入样例#3： 复制

5 2

1 2

2 3

3 4

4 5

输出样例#3： 复制

6

说明

10%的数据中，n ≤ 1000, K = 1；

30%的数据中，K = 1；

80%的数据中，每个村庄相邻的村庄数不超过 25；

90%的数据中，每个村庄相邻的村庄数不超过 150； 100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

---

题解

这是一颗树。

我们加一条边，就等于一个环上的边只需要走一次，其他要走两次。

k==1,我们加到直径。

k==2,我们又要多一个环。这个环可能与直径形成的环重合，那么重合的部分就要走两次。把树的直径取反，取反就等于走两遍。因为答案是2*(n-1)-直径1+1-直径2+1，让第二次的利益最大化。

顺带一句：有负边的直径要dp求。

---

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=2000001;
struct node{
    int to,v,nex;
}e[N<<1];
int head[N],num,dis[N];
int x[N],y[N],vis[N],ff[N];
int s,t,n,k,maxn1,maxn2;
int f[N],flag[N];
int read(){
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}

void add(int from,int to,int v){
    num++;
    e[num].to=to;
    e[num].v=v;
    e[num].nex=head[from];
    head[from]=num;
}

void dfs(int u,int fa){
    for(int i=head[u];i;i=e[i].nex){
        int v=e[i].to;if(v==fa)continue;ff[v]=u;
        dis[v]=dis[u]+e[i].v;dfs(v,u);
    }
}

void dp(int x){
    flag[x]=1;
    for(int i=head[x];i;i=e[i].nex){
        int v=e[i].to;if(flag[v])continue;
        dp(v);maxn2=max(maxn2,f[x]+f[v]+e[i].v);
        f[x]=max(f[x],f[v]+e[i].v);
    }
}

int main(){
    n=read();k=read();
    for(int i=1;i<n;i++){
        x[i]=read(),y[i]=read();
        add(x[i],y[i],1);add(y[i],x[i],1);
    }
    dfs(1,0);for(int i=1;i<=n;i++)
    {if(dis[i]>maxn1)maxn1=dis[i],s=i;ff[i]=dis[i]=0;}
    dfs(s,0);maxn1=0;
    for(int i=1;i<=n;i++)
    {if(dis[i]>maxn1)maxn1=dis[i],t=i;dis[i]=0;}
    if(k==1){printf("%d\n",2*(n-1)-maxn1+1);return 0;}

    int now=t;memset(e,0,sizeof(e));
    memset(head,0,sizeof(head));num=0;
    while(now){vis[now]=1;now=ff[now];}
    for(int i=1;i<n;i++)
    if(vis[x[i]]&&vis[y[i]])
    add(x[i],y[i],-1),add(y[i],x[i],-1);
    else add(x[i],y[i],1),add(y[i],x[i],1);
    memset(ff,0,sizeof(ff));s=0;
    dp(1);
    printf("%d\n",2*(n-1)-maxn1+1-maxn2+1);
    return 0;
}