[CTSC2016]单调上升路径

题目：UOJ#201。

题目大意：给定n个点（n是偶数）的完全图，现在要你给每条边确定一个权值（互不相等），使得最长的单调上升路径最短。现在要你输出边的权值。

一条路径被称为单调上升的，如果沿着它走时的权值是单调递增的。

解题思路：题目中的证明告诉我们一个结论：单调上升路径至少为n-1。

所以我们要让这个单调上升路径长度为n-1。

一张n个点的完全图可以拆成n-1个互不相等的，每个点的度数都为1的子图。例如

而每个这样的子图都走一条边，则刚好n-1。

那么我们对这样的一张子图，使它的所有边权值连续即可。

那么如何构造这样的图呢？

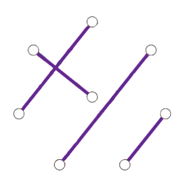
把这张子图的边转一下，点不变，就是一张新的、边不重复的子图。

所以如此构造出子图即可。

我的编号方法如下图，每次旋转时，点$a$对应的另一个点$p_a$就改为$(p_a+1)\mod(n-1)+1$即可（与中间的点n有关的点有一些不同，见代码）。

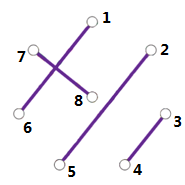
C++ Code：

#include<cstdio>
#include<cstring>
int n,p[505],num=0;
int e[505][505];
int main(){
	memset(e,0,sizeof e);
	scanf("%d",&n);
	for(int i=1;i<=n;++i)p[i]=n+1-i;
	for(int i=1;i<=n;++i)if(!e[i][p[i]])e[i][p[i]]=e[p[i]][i]=++num;
	for(int i=2;i<n;++i){
		for(int j=1;j<n;++j){
			if(i==j)p[j]=n;else
			if(p[j]==n){
				p[j]=(j+1)%(n-1)+1;
			}else
			p[j]=(p[j]+1)%(n-1)+1;
		}
		p[n]=i;
		for(int j=1;j<=n;++j)if(!e[j][p[j]])e[j][p[j]]=e[p[j]][j]=++num;
	}
	for(int i=1;i<n;++i){
		for(int j=i+1;j<n;++j)printf("%d ",e[i][j]);
		printf("%d\n",e[i][n]);
	}
	return 0;
}