自适应增强(Adaptive Boosting)

• 简介

AdaBoost，是英文”Adaptive Boosting“（自适应增强）的缩写，是一种迭代提升算法，其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这些弱分类器集合起来，构成一个更强的最终分类器(强分类器)。

它的自适应在于：其算法本身是通过改变数据分布来实现的，它根据每次训练集之中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练，最后将每次训练得到的分类器最后融合起来，作为最后的决策分类器。

• 基本思想

AdaBoost 的核心就是不断迭代训练弱分类器，并计算弱分类器的权重。需要注意的是，弱分类器的训练依赖于样本权重。每一轮迭代的样本权重都不相同，依赖于弱分类器的权重值和上一轮迭代的样本权重。具体过程如下：

1、训练当前迭代最优弱分类器

　　最优弱分类器是错误率最小的那个弱分类器。错误率的计算公式是：

　　

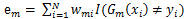
　　其中m = 1,2,..,M，代表第m轮迭代。i代表第i个样本。w 是样本权重。I指示函数取值为1或0，当I指示函数括号中的表达式为真时，I 函数结果为1；当I函数括号中的表达式为假时，I 函数结果为0。取错误率最低的弱分类器为当前迭代的最优弱分类器。

　　第一轮迭代计算时样本权重初始化为总样本数分之一。

2、计算最优弱分类器的权重

　　优弱分类器的权重只与该弱分类器的错误率有关。弱分类器的权重计算公式如下：

　　

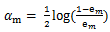
　　可以看出，错误率越小，则 alpha 值越大，即该弱分类器的权重越高；反之，错误率越大，则 alpha 值越小，则该弱分类器的权重越小。这样可以使分类精度高的弱分类器起到更大的作用，并削弱精度低的弱分类器的作用。

3、根据错误率更新样本权重

　　样本权重的更新与当前样本权重和弱分类器的权重有关。样本权重更新公式如下：

　　

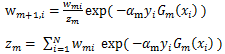
　　其中m = 1,2,..,M，代表第 m 轮迭代。i代表第i个样本。w 是样本权重。alpha 是弱分类器的权重。当样本被正确分类时，y 和 Gm 取值一致，则新样本权重变小；当样本被错误分类时，y 和 Gm 取值不一致，则新样本权重变大。这样处理，可以使被错误分类的样本权重变大，从而在下一轮迭代中得到重视。

4、迭代终止条件

　　不断重复1,2,3步骤，直到达到终止条件为止。终止条件是强分类器的错误率低于最低错误率阈值或达到最大迭代次数。

• 举例说明

数据集如表：

X	0	1	2	3	4	5
Y	1	1	-1	-1	1	-1

第一轮迭代

1、选择最优弱分类器

第一轮迭代时，样本权重初始化为（0.167, 0.167, 0.167, 0.167, 0.167, 0.167）。即1/6

表1数据集的切分点有0.5, 1.5, 2.5, 3.5, 4.5

若按0.5切分数据，得弱分类器x < 0.5,则 y = 1; x > 0.5, 则 y = -1。此时错误率为2 * 0.167 = 0.334

若按1.5切分数据，得弱分类器x < 1.5,则 y = 1; x > 1.5, 则 y = -1。此时错误率为1 * 0.167 = 0.167

若按2.5切分数据，得弱分类器x < 2.5,则 y = 1; x > 2.5, 则 y = -1。此时错误率为2 * 0.167 = 0.334

若按3.5切分数据，得弱分类器x < 3.5,则 y = 1; x > 3.5, 则 y = -1。此时错误率为3 * 0.167 = 0.501

若按4.5切分数据，得弱分类器x < 4.5,则 y = 1; x > 4.5, 则 y = -1。此时错误率为2 * 0.167 = 0.334

由于按1.5划分数据时错误率最小为0.167，则最优弱分类器为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。

2、计算最优弱分类器的权重

alpha = 0.5 * ln((1 – 0.167) / 0.167) = 0.8047

3、更新样本权重

x = 0, 1, 2, 3, 5时，y分类正确，则样本权重为：

0.167 * exp(-0.8047) = 0.075

x = 4时，y分类错误，则样本权重为：

0.167 * exp(0.8047) = 0.373

新样本权重总和为0.075 * 5 + 0.373 = 0.748

规范化后，

x = 0, 1, 2, 3, 5时，样本权重更新为：

0.075 / 0.748 = 0.10

x = 4时, 样本权重更新为：

0.373 / 0.748 = 0.50

综上，新的样本权重为(0.1, 0.1, 0.1, 0.1, 0.5, 0.1)。

此时强分类器为G(x) = 0.8047 * G1(x)。G1(x)为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。则强分类器的错误率为1 / 6 = 0.167。

第二轮迭代

1、选择最优弱分类器

若按0.5切分数据，得弱分类器x > 0.5,则 y = 1; x < 0.5, 则 y = -1。此时错误率为0.1 * 4 = 0.4

若按1.5切分数据，得弱分类器x < 1.5,则 y = 1; x > 1.5, 则 y = -1。此时错误率为1 * 0.5 = 0.5

若按2.5切分数据，得弱分类器x > 2.5,则 y = 1; x < 2.5, 则 y = -1。此时错误率为0.1 * 4 = 0.4

若按3.5切分数据，得弱分类器x > 3.5,则 y = 1; x < 3.5, 则 y = -1。此时错误率为0.1 * 3 = 0.3

若按4.5切分数据，得弱分类器x < 4.5,则 y = 1; x > 4.5, 则 y = -1。此时错误率为2 * 0.1 = 0.2

由于按4.5划分数据时错误率最小为0.2，则最优弱分类器为x < 4.5,则 y = 1; x > 4.5, 则 y = -1。

2、计算最优弱分类器的权重

alpha = 0.5 * ln((1 –0.2) / 0.2) = 0.6931

3、更新样本权重

x = 0, 1, 5时，y分类正确，则样本权重为：

0.1 * exp(-0.6931) = 0.05

x = 4 时，y分类正确，则样本权重为：

0.5 * exp(-0.6931) = 0.25

x = 2,3时，y分类错误，则样本权重为：

0.1 * exp(0.6931) = 0.20

新样本权重总和为 0.05 * 3 + 0.25 + 0.20 * 2 = 0.8

规范化后，

x = 0, 1, 5时，样本权重更新为：

0.05 / 0.8 = 0.0625

x = 4时, 样本权重更新为：

0.25 / 0.8 = 0.3125

x = 2, 3时, 样本权重更新为：

0.20 / 0.8 = 0.250

综上，新的样本权重为(0.0625, 0.0625, 0.250, 0.250, 0.3125, 0.0625)。

此时强分类器为G(x) = 0.8047 * G1(x) + 0.6931 * G2(x)。G1(x)为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。G2(x)为x < 4.5,则 y = 1; x > 4.5, 则 y = -1。

按G(x)分类会使x=4分类错误，则强分类器的错误率为1 / 6 = 0.167。

第三轮迭代

1、选择最优弱分类器

若按0.5切分数据，得弱分类器x < 0.5,则 y = 1; x > 0.5, 则 y = -1。此时错误率为0.0625 + 0.3125 = 0.375

若按1.5切分数据，得弱分类器x < 1.5,则 y = 1; x > 1.5, 则 y = -1。此时错误率为1 * 0.3125 = 0.3125

若按2.5切分数据，得弱分类器x > 2.5,则 y = 1; x < 2.5, 则 y = -1。此时错误率为0.0625 * 2 + 0.250 + 0.0625 = 0.4375

若按3.5切分数据，得弱分类器x > 3.5,则 y = 1; x < 3.5, 则 y = -1。此时错误率为0.0625 * 3 = 0.1875

若按4.5切分数据，得弱分类器x < 4.5,则 y = 1; x > 4.5, 则 y = -1。此时错误率为2 * 0.25 = 0.5

由于按3.5划分数据时错误率最小为0.1875，则最优弱分类器为x > 3.5,则 y = 1; x < 3.5, 则 y = -1。

2、计算最优弱分类器的权重

alpha = 0.5 * ln((1 –0.1875) / 0.1875) = 0.7332

3、更新样本权重

x = 2, 3时，y分类正确，则样本权重为：

0.25 * exp(-0.7332) = 0.1201

x = 4 时，y分类正确，则样本权重为：

0.3125 * exp(-0.7332) = 0.1501

x = 0, 1, 5时，y分类错误，则样本权重为：

0.0625 * exp(0.7332) = 0.1301

新样本权重总和为 0.1201 * 2 + 0.1501 + 0.1301 * 3 = 0.7806

规范化后，

x = 2, 3时，样本权重更新为：

0.1201 / 0.7806 = 0.1539

x = 4时, 样本权重更新为：

0.1501 / 0.7806 = 0.1923

x = 0, 1, 5时, 样本权重更新为：

0.1301 / 0.7806 = 0.1667

综上，新的样本权重为(0.1667, 0.1667, 0.1539, 0.1539, 0.1923, 0.1667)。

此时强分类器为G(x) = 0.8047 * G1(x) + 0.6931 * G2(x) + 0.7332 * G3(x)。

G1(x)为x < 1.5,则 y = 1; x > 1.5, 则 y = -1。

G2(x)为x < 4.5,则 y = 1; x > 4.5, 则 y = -1。

G3(x)为x > 3.5,则 y = 1; x < 3.5, 则 y = -1。

按G(x)分类所有样本均分类正确，则强分类器的错误率为0 / 6 = 0，则停止迭代。

最终强分类器为G(x) = 0.8047 * G1(x) + 0.6931 * G2(x) + 0.7332 * G3(x)。

• 代码实现

环境：MacOS mojave　　10.14.3

Python　　3.7.0

使用库：scikit-learn    0.19.2

sklearn.ensemble.AdaBoostClassifier官方库：https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html

AdaBoost.py　　主程序和算法

import matplotlib.pyplot as plt
from prep_terrain_data import makeTerrainData
from class_vis import prettyPicture

features_train, labels_train, features_test, labels_test = makeTerrainData()

### the training data (features_train, labels_train) have both "fast" and "slow"
### points mixed together--separate them so we can give them different colors
### in the scatterplot and identify them visually
grade_fast = [features_train[ii][0] for ii in range(0, len(features_train)) if labels_train[ii]==0]
bumpy_fast = [features_train[ii][1] for ii in range(0, len(features_train)) if labels_train[ii]==0]
grade_slow = [features_train[ii][0] for ii in range(0, len(features_train)) if labels_train[ii]==1]
bumpy_slow = [features_train[ii][1] for ii in range(0, len(features_train)) if labels_train[ii]==1]

#### initial visualization
plt.xlim(0.0, 1.0)
plt.ylim(0.0, 1.0)
plt.scatter(bumpy_fast, grade_fast, color = "b", label="fast")
plt.scatter(grade_slow, bumpy_slow, color = "r", label="slow")
plt.legend()
plt.xlabel("bumpiness")
plt.ylabel("grade")

################################################################################

### your code here!  name your classifier object clf if you want the
### visualization code (prettyPicture) to show you the decision boundary
from sklearn.ensemble import AdaBoostClassifier

clf = AdaBoostClassifier(n_estimators=100)
clf.fit(features_train,labels_train)

prettyPicture(clf, features_test, labels_test)
accuracy = clf.score(features_test, labels_test)
print (accuracy)

plt.show()

class_vis.py　　绘图与保存图像

import numpy as np
import matplotlib.pyplot as plt
import pylab as pl

def prettyPicture(clf, X_test, y_test):
    x_min = 0.0; x_max = 1.0
    y_min = 0.0; y_max = 1.0

    # Plot the decision boundary. For that, we will assign a color to each
    # point in the mesh [x_min, m_max]x[y_min, y_max].
    h = .01  # step size in the mesh
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())

    plt.pcolormesh(xx, yy, Z, cmap=pl.cm.seismic)

    # Plot also the test points
    grade_sig = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==0]
    bumpy_sig = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==0]
    grade_bkg = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==1]
    bumpy_bkg = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==1]

    plt.scatter(grade_sig, bumpy_sig, color = "b", )
    plt.scatter(grade_bkg, bumpy_bkg, color = "r",)
    plt.legend()
    plt.xlabel("bumpiness")
    plt.ylabel("grade")

    plt.savefig("test.png")
                                    

perp_terrain_data.py　　生成训练点

import random

def makeTerrainData(n_points=1000):
###############################################################################
### make the toy dataset
    random.seed(42)
    grade = [random.random() for ii in range(0,n_points)]
    bumpy = [random.random() for ii in range(0,n_points)]
    error = [random.random() for ii in range(0,n_points)]
    y = [round(grade[ii]*bumpy[ii]+0.3+0.1*error[ii]) for ii in range(0,n_points)]
    for ii in range(0, len(y)):
        if grade[ii]>0.8 or bumpy[ii]>0.8:
            y[ii] = 1.0

### split into train/test sets
    X = [[gg, ss] for gg, ss in zip(grade, bumpy)]
    split = int(0.75*n_points)
    X_train = X[0:split]
    X_test  = X[split:]
    y_train = y[0:split]
    y_test  = y[split:]

    grade_sig = [X_train[ii][0] for ii in range(0, len(X_train)) if y_train[ii]==0]
    bumpy_sig = [X_train[ii][1] for ii in range(0, len(X_train)) if y_train[ii]==0]
    grade_bkg = [X_train[ii][0] for ii in range(0, len(X_train)) if y_train[ii]==1]
    bumpy_bkg = [X_train[ii][1] for ii in range(0, len(X_train)) if y_train[ii]==1]

    training_data = {"fast":{"grade":grade_sig, "bumpiness":bumpy_sig}
            , "slow":{"grade":grade_bkg, "bumpiness":bumpy_bkg}}

    grade_sig = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==0]
    bumpy_sig = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==0]
    grade_bkg = [X_test[ii][0] for ii in range(0, len(X_test)) if y_test[ii]==1]
    bumpy_bkg = [X_test[ii][1] for ii in range(0, len(X_test)) if y_test[ii]==1]

    test_data = {"fast":{"grade":grade_sig, "bumpiness":bumpy_sig}
            , "slow":{"grade":grade_bkg, "bumpiness":bumpy_bkg}}

    return X_train, y_train, X_test, y_test

得到结果，正确率为92.4%

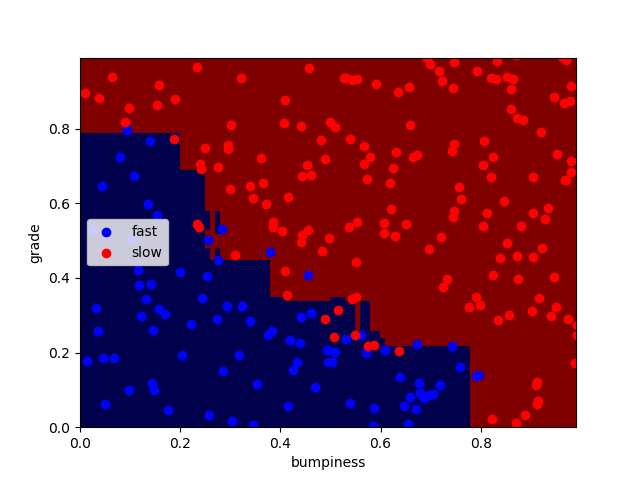
Adaboost的参数

n_estimators表示迭代的次数

n_estimators分别为100、1000、10000时：

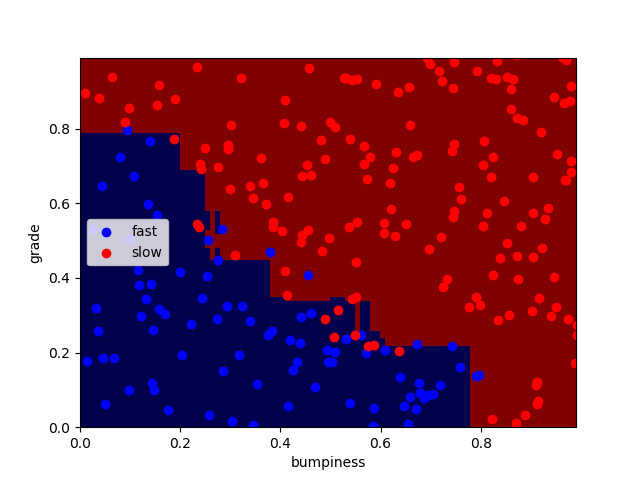
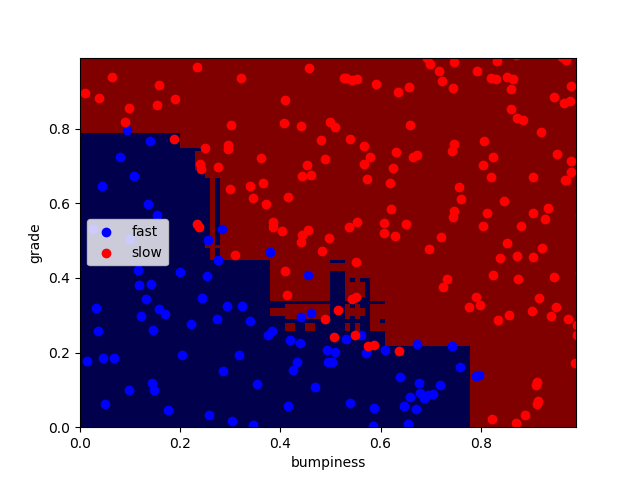
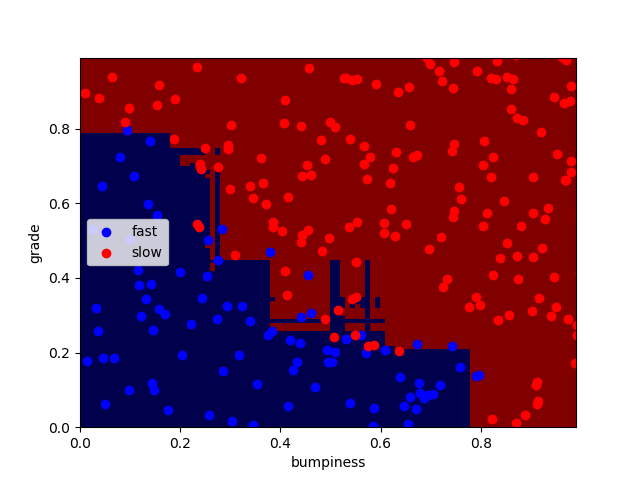
正确率分别为：92.4%　　91.6%　　92%

可以看出迭代次数越大，过拟合现象越严重，但正确率并无明显变化，编译时间略微增加。

• AdaBoost优缺点

优点：

1、可以将不同的分类算法作为弱分类器。

2、AdaBoost充分考虑的每个分类器的权重。

缺点：

1、AdaBoost迭代次数也就是弱分类器数目不太好设定。

2、数据不平衡导致分类精度下降。

3、训练比较耗时，