dp——01背包

今天学习了01背包不算是复习吧，发现完全不会状态之间的转移如此让我捉摸不透尽管很简单但本人觉得还是很难，奇怪地拐点也很难被发现。知道01背包二维的话是很慢的，然后就是非得先打二维毕竟一维是根据二维的想法进行优化的所以决定先啃二维结果漏洞百出，首先呢就是循环顺序了，因为是用前一个被更新过得最优解来更新当前的解所以第二重循环（容量）是可以倒着或者正着来写的。

for(int i=;i<=n;i++)
    {
        for(int j=m;j>=;j--)
        {
            f[i][j]=f[i-][j];
            if(j>=w[i])
            f[i][j]=max(f[i-][j-w[i]]+v[i],f[i][j]);
        }
    }

for(int i=;i<=n;i++)
    {
        for(int j=;j<=m;j++)
        {
            f[i][j]=f[i-][j];
            if(j>=w[i])
            f[i][j]=max(f[i-][j-w[i]]+v[i],f[i][j]);
        }
    }

不管是正着枚举还是倒着枚举都是合法的然后我就发现了f[i][j]有一部分是通过f[i-1][j]枚举过来的所以代码就打成了这样子。

样例为

4 6
2 4
2 6
3 12
2 7

自己手动模拟会对本文的理解更深刻。。。

for(int i=;i<=n;i++)
    {
        for(int j=w[i];j<=m;j++)
        {
            f[i][j]=max(f[i-][j-w[i]]+v[i],f[i-][j]);
        }
    }

但这样子是错误的因为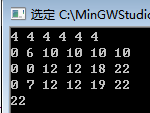前端的最优值并没有被附上去所以我想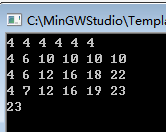很明显我的局部最优解并没有被求出所以导致答案不是最优的，因为01背包靠的是前端的最优解推出末端最优解所以一旦前端的值被w[i]卡掉所以后面的值就不是最优的了，这是我自己打出来的一个错误加深了对01的理解和感触比之前强多了，因为之前总是不明白dp的状态转移之间的规律所以感觉很模糊真正的自己去模拟一遍这个dp的过程会发现很简单。

于是乎我开始了瞎搞因为lyd书上说可以把f数组全部赋值为0xcf，f[0][0]=0,状态即可开始转移然后我就这样打了然后wa了好多慢慢继续打表学长，学长也研究了好大一会才发现它的状态转移是不完全的，差了一个状态f[i][j]=max(f[i][j],f[i][j-1]);于是就这样具体看打表出来的结果。

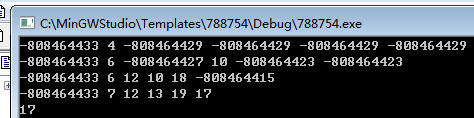这个地方明明最优值是19却没有转移过来，发现了问题的所在，如果是一个正解的背包那么f[n][m]里面存的应该是最优解所以出锅了，然后发现最后的值是由10转移而来而这个10在它的那个状态并不是最优解因为在10的前面有一个12,考虑一下10的转移它是因为i-1对应是负无穷所以状态无法转移到当前的值这个地方是很绕的，应该是12的所以最优解就会变化，但是呢在这个地方书上说最优解是在f[n][j]之中书上没毛病所以最好便利一遍找到max即可，看书不认真啊自己。

于是乎洛谷一道01背包由于m过大空间限制O(m*n)直接mle了，所以呢考虑优化空间，书是开了一个滚动数组来节约空间，这个不算很复杂但以后有时间再补充，书上还有一种是01背包的解法将至一维，因为f[i][j]只与f[i-1][j-w[i]]和f[i-1][j]有关所以考虑倒着推就可以使用还没有被更新过得那个f[j]了，这样二维骤降一维。省空间，没有时间换空间哦！

下面是代码：

#include<ctime>
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdio>
#include<iomanip>
#include<map>
#include<queue>
#include<stack>
#include<cstring>
#include<string>
#include<vector>
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
int m,n;
int f[];
int w[],v[];
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=;i<=n;i++)
    {
        w[i]=read();v[i]=read();
    }
    for(int i=;i<=n;i++)
    {
        for(int j=m;j>=w[i];j--)
        {
            f[j]=max(f[j],f[j-w[i]]+v[i]);
        }
    }
    printf("%d\n",f[m]);
    return ;
}

当然01背包这么好的东西可不止这一点，还有一道比较奇怪地01背包。。建议思考如何转移。

原本以为是一道很难的树形dp，结果自己就被骗了，真坑。。

这道题是个01背包，不过形势不太相同我认为。但转移的时候用了点高级的技巧，也算是炫技的一种吧，一行状态转移！

#include<iostream>
#include<cmath>
#include<cstring>
#include<string>
#include<ctime>
#include<iomanip>
#include<cstdio>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
#include<map>
#define inf 1000000002
using namespace std;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
int n,s;
struct wy
{
    int x,y;
}t[maxn];
int f[];
int main()
{
    //freopen("1.in","r",stdin);
    s=read();n=read();
    for(int i=;i<=n;i++)t[i].x=read(),t[i].y=read();
    for(int i=;i<=s;i++)f[i]=inf;f[]=;
    for(int i=;i<=n;i++)
    {
        for(int j=s;j>=;j--)
        {
            if(j>=t[i].x&&f[j-t[i].x]!=inf)f[j]=max(f[j]==inf?:f[j],min(f[j-t[i].x]>?f[j-t[i].x]:inf,t[i].y));
        }
    }
    printf("%d\n",f[s]);
    return ;
}

0.0

云水生涯，不是梦，潋滟人生，不成空！