【Codeforces 949D】Shake It! 【动态规划】

参考： http://blog.csdn.net/gjghfd/article/details/77824901

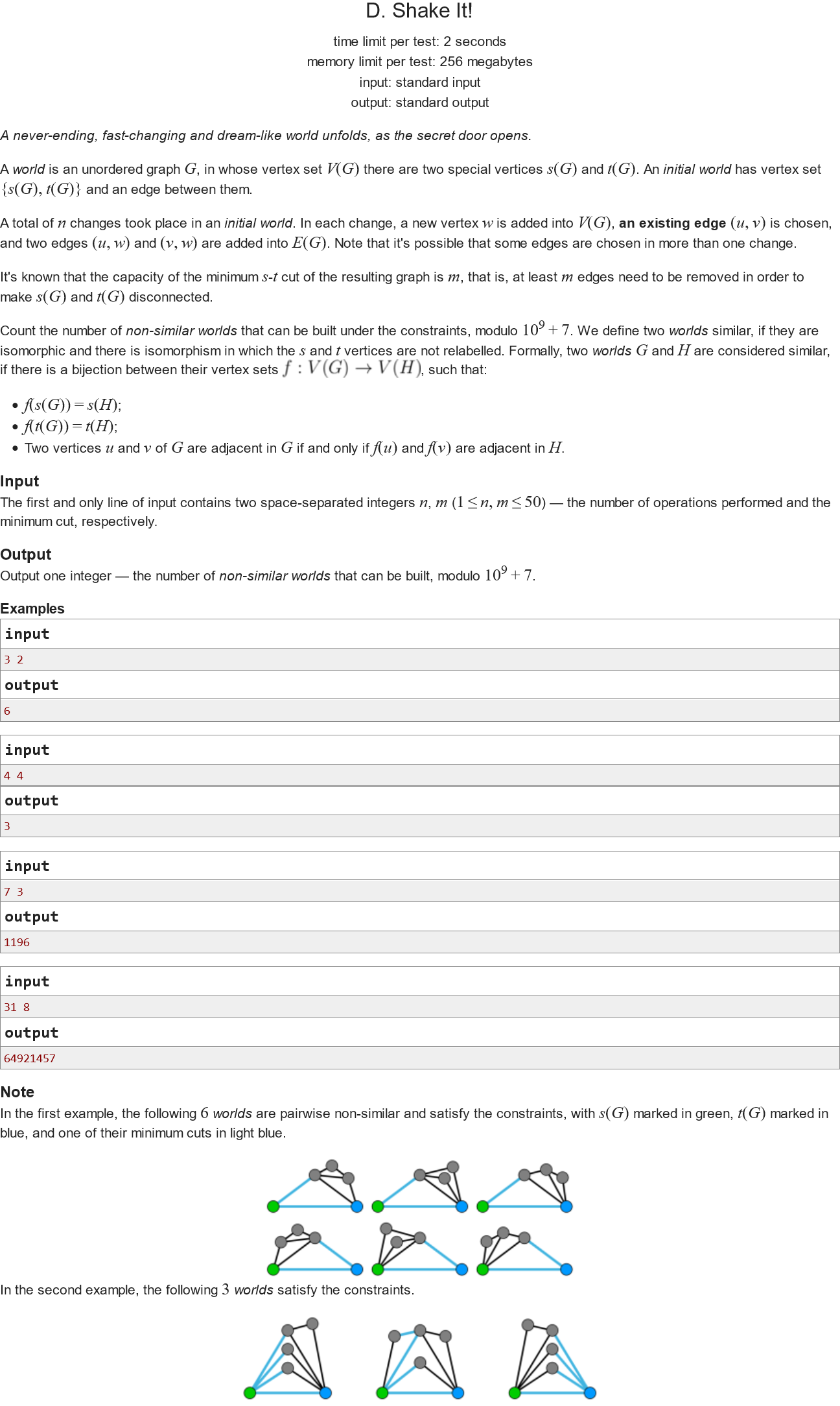
所求的是满足条件的图中“不同构”的数量，意味着操作的顺序是可以忽略的。考虑若干次操作后得到的一个“World” G，其中某次操作(s(G), t(G))生成的节点为w，则由s(G)到w和由w到t(G)的所有路径及途径点生成的两个子图分别符合“World”的定义。

这意味着我们可以将一个“World”分割成若干个子问题来求解。

不妨令F(N, M)表示经N次操作后得到的s(G)与t(G)之间最小割为M的所有不同构的G的数量。考虑N次操作中所有基于u=s(G), v=t(G)的操作生成的子“world”，如图所示：

则有$$N = \sum_i (a_i + c_i + 1) \\ M = \sum_i \min\{b, d\} $$

由此可以按照a, b, c, d对这些成对的子世界分类，令$$g(i, j) = \sum_{a+c+1=i \land min\{b, d\} = j} F(a, b) * F(c, d) $$

这样我们就可以类比背包问题的求解过程，从小到大依次求出g(i, j)，并用g(i, j)更新F的答案。

考虑当前要将t组在g(i, j)中的“子世界对”放入背包，而F(x,y)是尚未考虑将g(i, j)作为子世界的情况的世界数量，那么状态转移的过程就相当于在g(i,j)中可重复地选取t个子世界对，使得总操作数变为x+t*i，总割集变为y+t*j。由于“同构”的定义不考虑操作的顺序，上述转移的方案数应为$\binom{g(i, j) + t - 1}{t} $

即状态转移为$$F(x, y) \cdot \binom{g(i, j) + t - 1}{t} \Longrightarrow F(x+t*i, y+t*j)$$

代码实现如下

 By Asm.Def, contest: Codeforces Round # (Div. ), problem: (D) Shake It!, Accepted, #

 #include <bits/stdc++.h>
 using namespace std;
 const int maxn = , mod = ;
 typedef long long LL;
 int N, M, F[maxn][maxn], G[maxn][maxn], inv[maxn];

 void init()
 {
     scanf("%d%d", &N, &M);
     inv[] = ;
     for(int i = ;i < maxn;++i)
         inv[i] = LL(mod-mod/i) * inv[mod%i] % mod;
 }
 void work()
 {
     F[][] = ;
     for(int i = ;i <= N;++i) for(int j = ;j < maxn;++j)
     {
         for(int a = ;a < i;++a)
         {
             G[i][j] = (G[i][j] + (LL) F[a][j] * F[i--a][j]) % mod;
             for(int b = j+;b <= i+ && b < maxn;++b)
             {
                 G[i][j] = (G[i][j] + (LL) F[a][b] * F[i--a][j]) % mod;
                 G[i][j] = (G[i][j] + (LL) F[a][j] * F[i--a][b]) % mod;
             }
         }
         //get G[i][j]
         for(int x = N-;x >= ;--x) for(int y = ;y < maxn;++y) if(F[x][y])
         {
             int C = ;
             for(int t = ;x+t*i <= N && y+t*j < maxn;++t)
             {
                 C = (LL) C * (G[i][j]-+t) % mod * inv[t] % mod;
                 F[x+t*i][y+t*j] = (F[x+t*i][y+t*j] + (LL) F[x][y] * C) % mod;
             }
         }
     }
     printf("%d\n", F[N][M]);
 }
 int main()
 {
     init();
     work();
     return ;
 }

动态规划