回归损失函数2 ： HUber loss,Log Cosh Loss,以及 Quantile Loss

均方误差（Mean Square Error,MSE）和平均绝对误差（Mean Absolute Error,MAE) 是回归中最常用的两个损失函数，但是其各有优缺点。为了避免MAE和MSE各自的优缺点，在Faster R-CNN和SSD中使用$\text{Smooth} L_1$损失函数，当误差在$[-1,1]$ 之间时，$\text{Smooth} L_1$损失函数近似于MSE，能够快速的收敛；在其他的区间则近似于MAE，其导数为$\pm1$，不会对离群值敏感。

本文再介绍几种回归常用的损失函数

Huber Loss
Log-Cosh Loss
Quantile Loss

Huber Loss

Huber损失函数（$\text{Smooth} L_1$损失函数是其的一个特例）整合了MAE和MSE各自的优点，并避免其缺点
\[
L_\delta(y,f(x)) = \left \{ \begin{array}{c} \frac{1}{2} (y - f(x))^2 & \mid y - f(x) \mid \leq \delta \\ \delta \mid y-f(x) \mid - \frac{1}{2} \delta ^2 & \text{otherwise}\end{array}\right.
\]

$\delta$ 是Huber的一个超参数，当真实值和预测值的差值$\mid y- f(x) \mid \leq \delta$ 时，Huber就是MSE；当差值在$(-\infty,\delta )$或者 $(\delta,+\infty)$ 时，Huber就是MAE。这样，当误差较大时，使用MAE对离群点不那么敏感；在误差较小时使用MSE，能够快速的收敛；

这里超参数$\delta$的值的设定就较为重要，和真实值的差值超过该值的样本为异常值。误差的绝对值小于$\delta$ 时，使用MSE；当误差大于$\delta$ 时，使用MAE。

下图给出了不同的$\delta$ 值，Huber的函数曲线。

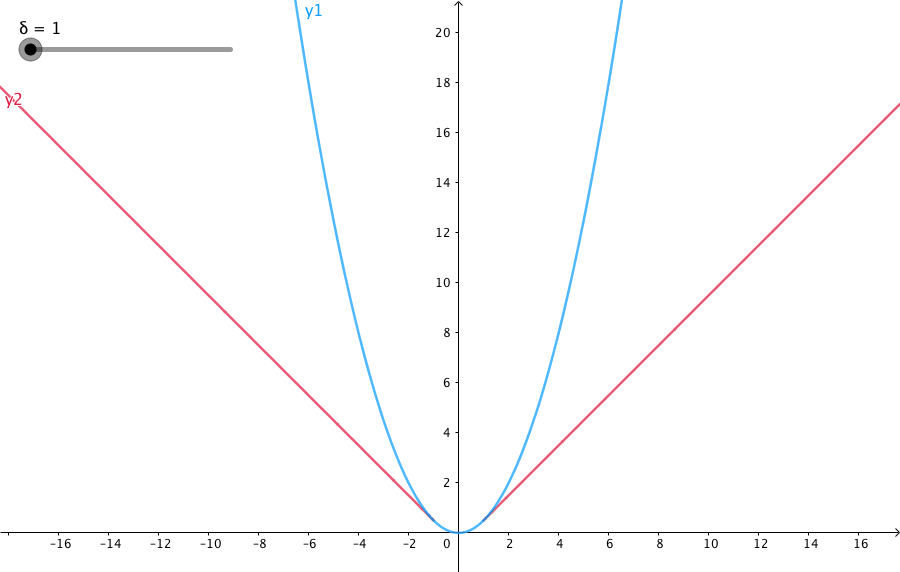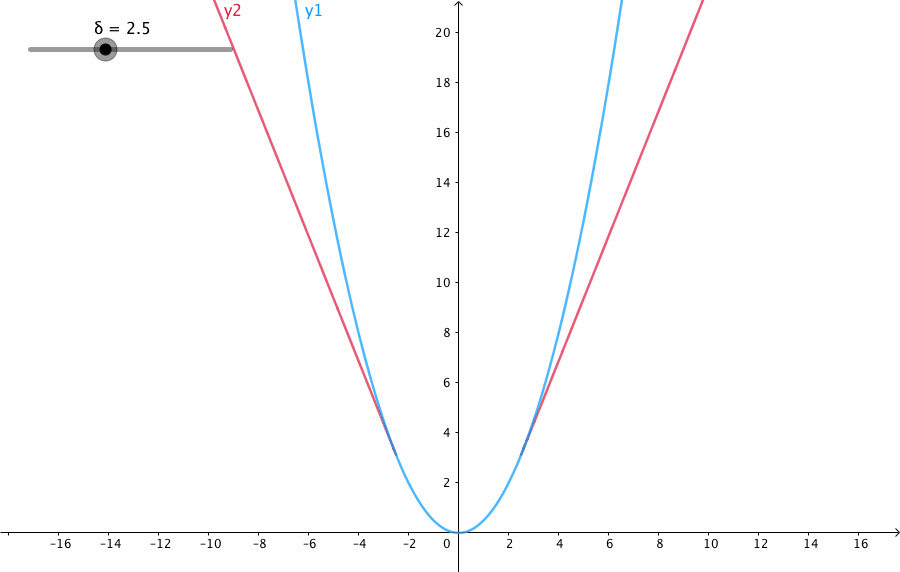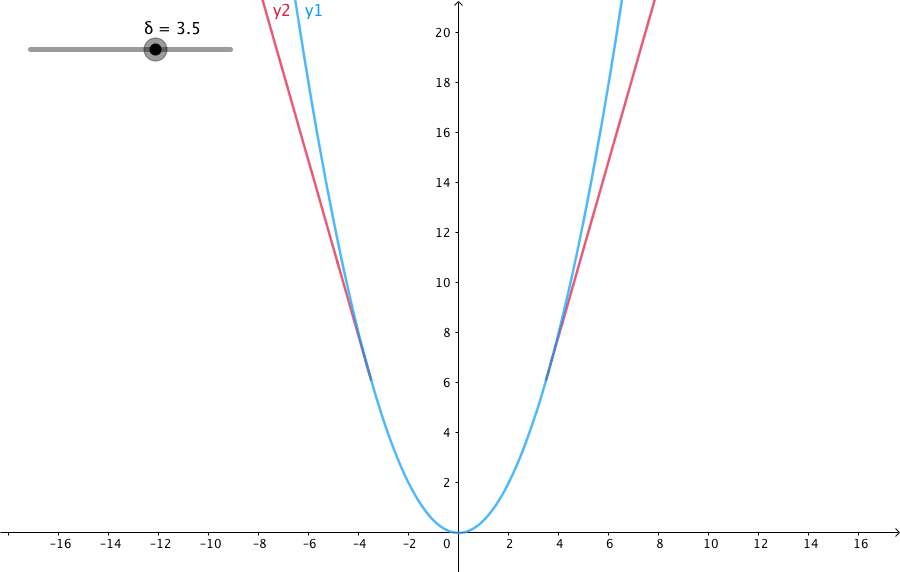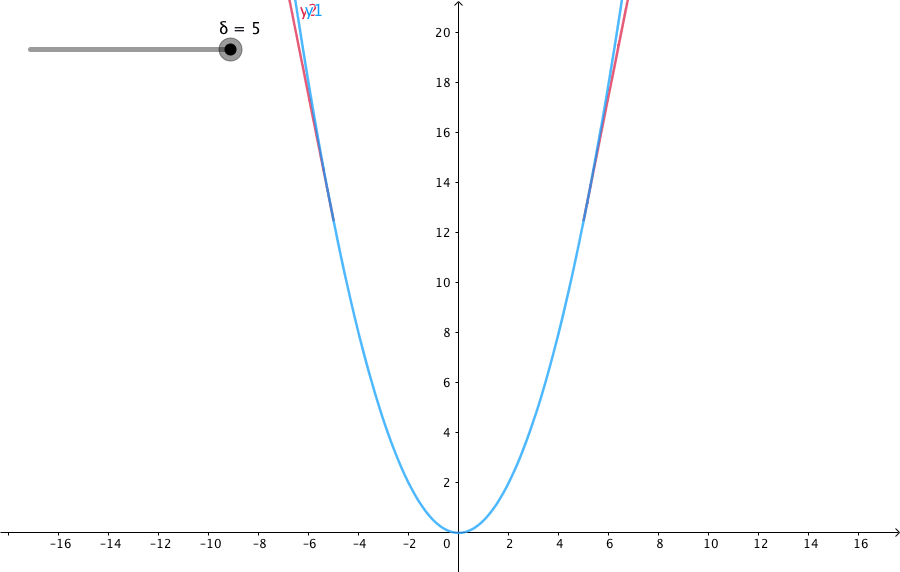
横轴表示真实值和预测值的差值，纵轴为Huber的函数值。可以看出，$\delta$ 越小其曲线越趋近于MSE；越大，越趋近于MAE。

另外，使用MAE训练神经网络最大的一个问题就是不变的大梯度，这可能导致在使用梯度下降快要结束时，错过了最小点。而对于MSE，梯度会随着损失的减小而减小，使结果更加精确。

在这种情况下，Huber损失就非常有用。它会由于梯度的减小而落在最小值附近。比起MSE，它对异常点更加鲁棒。因此，Huber损失结合了MSE和MAE的优点。但是，Huber损失的问题是我们可能需要不断调整超参数$\delta$ 。

$\text{Smooth }L_1$ 损失函数可以看作超参数$\delta = 1$ 的Huber函数。

Log-Cosh Loss

Log-Cosh是比$L_2$ 更光滑的损失函数，是误差值的双曲余弦的对数
\[
L(y,f(x)) = \sum_{i=1}^n\log \cosh(y-f(x))
\]
其中，$y$为真实值，$f(x)$ 为预测值。

对于较小的误差$\mid y - f(x) \mid $ ，其近似于MSE，收敛下降较快；对于较大的误差$\mid y - f(x) \mid$ 其近似等于$\mid y-f(x) \mid - log(2)$ ,类似于MAE，不会受到离群点的影响。 Log-Cosh具有Huber 损失的所有有点，且不需要设定超参数。

相比于Huber,Log-Cosh求导比较复杂，计算量较大，在深度学习中使用不多。不过，Log-Cosh处处二阶可微，这在一些机器学习模型中，还是很有用的。例如XGBoost，就是采用牛顿法来寻找最优点。而牛顿法就需要求解二阶导数（Hessian）。因此对于诸如XGBoost这类机器学习框架，损失函数的二阶可微是很有必要的。但Log-cosh损失也并非完美，其仍存在某些问题。比如误差很大的话，一阶梯度和Hessian会变成定值，这就导致XGBoost出现缺少分裂点的情况。

Quantile Loss 分位数损失

通常的回归算法是拟合训练数据的期望或者中位数，而使用分位数损失函数可以通过给定不同的分位点，拟合训练数据的不同分位数。如下图

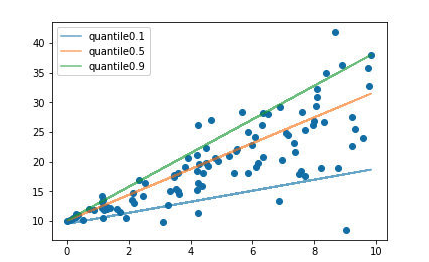
设置不同的分位数可以拟合出不同的直线。

分位数损失函数如下：
\[
L_{quantile} = \frac{1}{N}\sum_{i=1}^N \amalg_{y > f(x)}(1-\gamma)\mid y-f(x)\mid + \amalg_{y < f(x)}\gamma \mid y - f(x) \mid
\]
该函数是一个分段函数，$\gamma$ 为分位数系数，$y$为真实值，$f(x)$为预测值。根据预测值和真实值的大小，分两种情况来开考虑。$y > f(x)$ 为高估，预测值比真实值大；$y < f(x)$为低估，预测值比真实值小，使用不同过得系数来控制高估和低估在整个损失值的权重 。

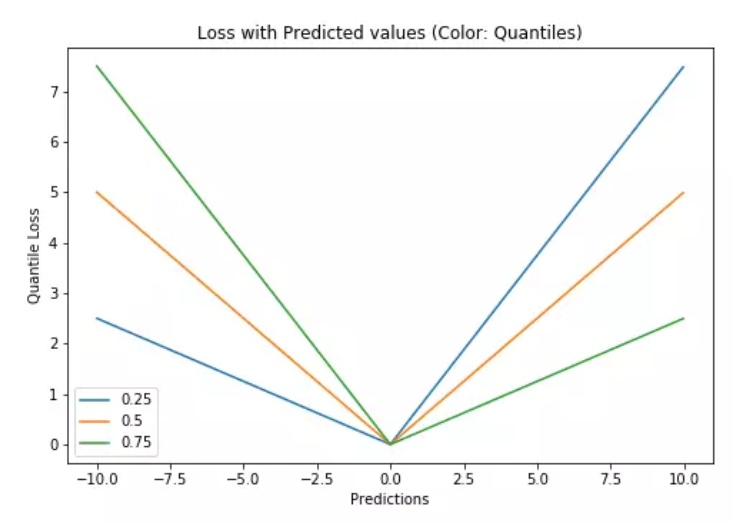
特别的，当$\gamma = 0.5$ 时，分位数损失退化为平均绝对误差MAE，也可以将MAE看成是分位数损失的一个特例 - 中位数损失。下图是取不同的中位点$[0.25,0.5,0.7]$ 得到不同的分位数损失函数的曲线，也可以看出0.5时就是MAE。

总结

均方误差（Mean Square Error,MSE）和平均绝对误差（Mean Absolute Error,MAE) 可以说是回归损失函数的基础。但是MSE对对离群点（异常值）较敏感，MAE在梯度下降的过程中收敛较慢，就出现各种样的分段损失函数，在loss值较小的区间使用MSE，loss值较大的区间使用MAE。

Huber Loss ，需要一个超参数$\delta$ ,来定义离群值。$ \text{smooth } L_1$ 是$\delta = 1$ 的一种情况。
Log-Cosh Loss, Log-Cosh是比$L_2$ 更光滑的损失函数，是误差值的双曲余弦的对数.
Quantile Loss , 分位数损失，则可以设置不同的分位点，控制高估和低估在loss中占的比重。