特殊方格棋盘【状压DP】

特殊方格棋盘【状压DP】

讲真状压DP这个东西只不过是有那么亿丢丢考验心态罢了（确信）

先从板子题说起，另加一些基础知识

题目描述

在的方格棋盘上放置n 个车，某些格子不能放，求使它们不能互相攻击的方案总数。

注意：同一行或同一列只能有一个车，否则会相互攻击

输入格式

输入文件第一行，有两个数n, m ,n表示方格棋盘大小,m表示不能放的格子数量

下面有m行,每行两个整数,为不能放的格子的位置。

输出格式

输出文件也只有一行，即得出的方案总数。

样例

样例输入

2 1
1 1

样例输出

1

---

思路分析

状压的核心：1. 二进制表示状态

​ 2.位运算进行转移等操作

• 状压DP的核心就在于用二进制数表示一种状态，其实是一种非常暴力的算法，举个例子：

  例如dp[s] [v]中，S可以代表已经访问过的顶点的集合，v可以代表当前所在的顶点为v。S代表的就是一种状态（二进制表示），比如 (11001)2 代表在二进制中{0，3，4}三个顶点已经访问过了，(11001)2 代表的十进制数就是25 ，所以当S为25的时候其实就是代表已经访问过了{0，3，4}三个顶点，那假如一共有5个顶点（标号为01234）的话，所有的顶点都访问完毕应该S为什么呢？是　(11111)2。

• 关于本题：

  • 这题的约束条件非常非常简单，直接告诉了你哪里不能放，那么我们怎么记录这个所给的约束条件呢？

  • 其实也是用二进制的思想，我们开一个数组a[x]，表示第x行的限制，如果第x行的第y列不能放置，那么我们就将其对应的二进制位变为1，这里涉及到了位运算——a[x] += 1<<(y-1);

  • 本题还用到了另一个和二进制紧密相关的东西：

    int lowbit(int x){return x & -x;}
    返回值是最后一个二进制数位为1的位置
    

• 转移方程：

  int maxs = 1<<n; //显然这是最大的状态，即每个二进制位都是1
  for(int s = 1;s < maxs;s++){
  	int cnt = 0;
  	for(int i = s;i;i-=lowbit(i))cnt++;//记录二进制1的个数，即放车车的个数（等于行数）
  	for(int i = s;i;i-=lowbit(i)){ //根据不能放在同一列进行转移
  		if(!(a[cnt] & lowbit(i))){ //首先要保证该位置可以放
  			int ss = s^lowbit(i); //异或恰好使得上一行的状态与本行不发生冲突
  			f[s] += f[ss];
  		}
  	}
  }
  

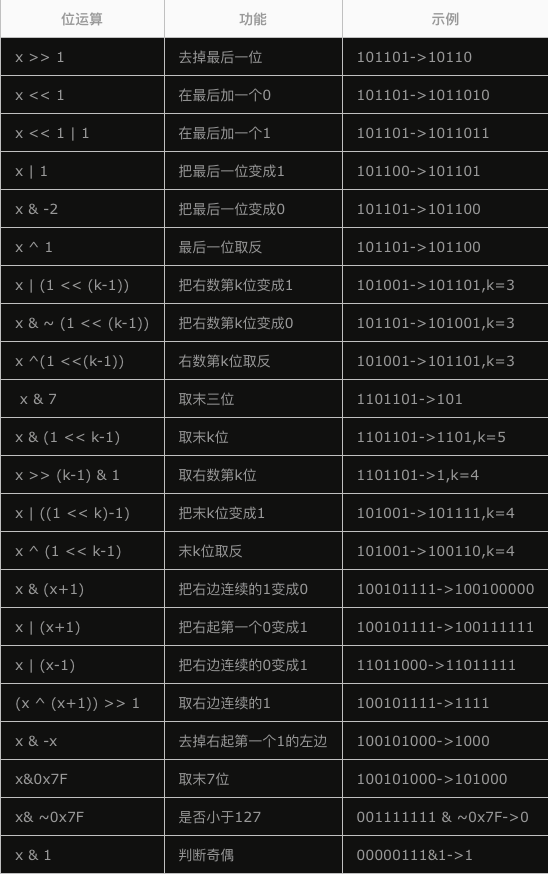
  另附一张位运算常用操作：

  

  上代码

  #include <cstdio>
  #include <cstring>
  #include <iostream>
  #include <algorithm>
  
  const int  maxn = (1<<20)-1;
  typedef long long ll;
  ll f[maxn],a[25];
  
  int lowbit(int x){
  	return x & -x;
  }
  
  int main(){
  	int n,m;scanf("%d%d",&n,&m);
  	for(int i = 1;i <= m;i++){
  		int x,y;scanf("%d%d",&x,&y);
  		a[x] += 1<<(y-1);
  	}
  	f[0] = 1;
  	int maxs = 1<<n;
  	for(int s = 1;s < maxs;s++){
  		int cnt = 0;
  		for(int i = s;i;i-=lowbit(i))cnt++;
  		for(int i = s;i;i-=lowbit(i)){
  			if(!(a[cnt] & lowbit(i))){
  				int ss = s^lowbit(i);
  				f[s] += f[ss];
  			}
  		}
  	}
  	printf("%lld\n",f[maxs - 1]);
  	return 0;
  }
  

发量成功减1%