[luogu2680] 运输计划 (lca+二分+树上差分)

传送门

Description

Input

Output

一个整数，表示小 P 的物流公司完成阶段性工作所需要的最短时间。

Sample Input

6 3

1 2 3

1 6 4

3 1 7

4 3 6

3 5 5

3 6

2 5

4 5

Sample Output

11

HINT

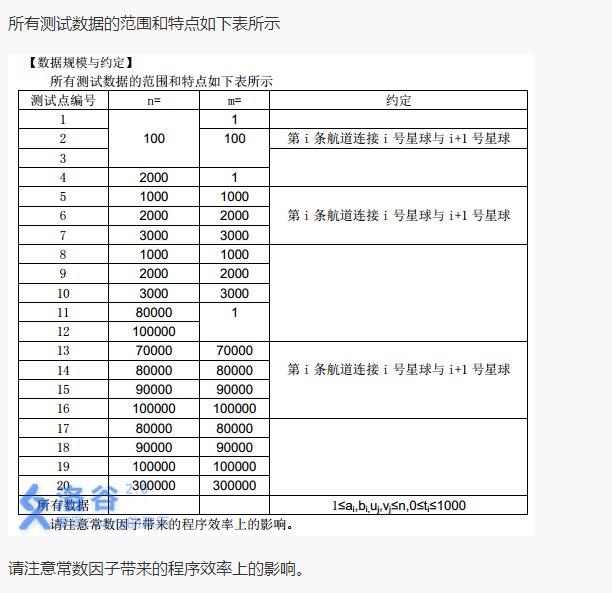
Solution

很显然第一步是求出lca然后求出每个运输计划的长度

题目要求一个时间最大值的最小值 很明显要二分

二分一个运输时间，统计所有超过这个时间的运输计划经过的路径

找出其中被所有超时计划包括的最大路径 直接判断就行

lca和长度我用的tarjan

统计每条路径的经过次数那就树上差分喽(￣▽￣)／

Code

//By Menteur_Hxy
#include<cstdio>
#include<vector>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define M(a,b) memset(a,(b),sizeof(a))
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
#define E(i,u) for(register int i=head[u];i;i=nxt[i])
using namespace std;

int read() {
	int x=0,f=1; char c=getchar();
	while(!isdigit(c)) {if(c=='-')f=-f; c=getchar();}
	while(isdigit(c)) x=(x<<1)+(x<<3)+c-48,c=getchar();
	return x*f;
}

const int N=300010;
bool vis[N];
int n,m,ecnt,maxlen,res,num;
int nxt[N<<1],to[N<<1],w[N<<1],head[N],ln[N],rn[N],len[N],lca[N],dis[N],fa[N],sum[N],cnt[N];
vector <int> V[N];

int getf(int x) {return fa[x]==x?x:fa[x]=getf(fa[x]);}

void tarjan(int u,int pre) {
	E(i,u) { int v=to[i];
		if(v==pre) continue;
		dis[v]=dis[u]+w[i];
		tarjan(v,u);
		cnt[v]=w[i];//差分时用
	}
	int siz=V[u].size();
	F(i,0,siz-1) {
		int id=V[u][i],v=ln[id]==u?rn[id]:ln[id];
		if(!vis[v]) continue;
		lca[id]=getf(v);
		len[id]=dis[v]+dis[u]-2*dis[lca[id]];
		maxlen=max(len[id],maxlen);
	}
	vis[u]=1;fa[u]=pre;
}

void dfs(int u,int pre) {
	E(i,u) { int v=to[i];
		if(v==pre) continue;
		dfs(v,u);
		sum[u]+=sum[v];
	}
	if(sum[u]==num&&cnt[u]>res) res=cnt[u];
}

bool jud(int t) {
	num=res=0;
	M(sum,0);
	F(i,1,m) if(len[i]>t) sum[ln[i]]++,sum[rn[i]]++,sum[lca[i]]-=2,num++;
	if(num==0) return 1;
	dfs(1,0);
	return maxlen-res<=t;
}

#define add(a,b,c) nxt[++ecnt]=head[a],to[ecnt]=b,head[a]=ecnt,w[ecnt]=c
#define ins(a,b,c) add(a,b,c),add(b,a,c)
int main() {
	n=read(),m=read();
	F(i,1,n) fa[i]=i;
	F(i,1,n-1) {
		int a=read(),b=read(),c=read();
		ins(a,b,c);
	}
	F(i,1,m) {
		int a=read(),b=read();
		ln[i]=a,rn[i]=b;
		V[a].push_back(i);
		V[b].push_back(i);
	}
	tarjan(1,0);
//	F(i,1,m) cout<<lca[i]<<" "<<len[i]<<endl;
	int l=0,r=maxlen;
	int ans=0x3f3f3f3f;
	while(l<=r) {
		int mid=(l+r)>>1;
		if(jud(mid)) ans=min(ans,mid),r=mid-1;
		else l=mid+1;
	}
	printf("%d",ans);
	return 0;
}