hdu 1410(直线与矩形相交)

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 13528		Accepted: 3521

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example:

line: start point: (4,9)

end point: (11,2)

rectangle: left-top: (1,5)

right-bottom: (7,1)

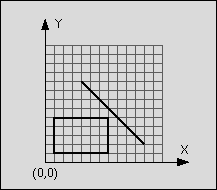
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the
rectangle have at least one point in common. The rectangle consists of
four straight lines and the area in between. Although all input values
are integer numbers, valid intersection points do not have to lay on the
integer grid.

Input

The
input consists of n test cases. The first line of the input file
contains the number n. Each following line contains one test case of the
format:

xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point
of the line and (xleft, ytop) the top left and (xright, ybottom) the
bottom right corner of the rectangle. The eight numbers are separated by
a blank. The terms top left and bottom right do not imply any ordering
of coordinates.

Output

For
each test case in the input file, the output file should contain a line
consisting either of the letter "T" if the line segment intersects the
rectangle or the letter "F" if the line segment does not intersect the
rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

今天又懂了一个~~非规范相交.
规范相交模板(两条线段只有一个交点):

///叉积
double mult(Point a, Point b, Point c)
{
    return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
}

///a, b为一条线段两端点c, d为另一条线段的两端点 相交返回true, 不相交返回false
bool isCross(Point a, Point b, Point c, Point d)
{
    if (max(a.x,b.x)<min(c.x,d.x))return false;
    if (max(a.y,b.y)<min(c.y,d.y))return false;
    if (max(c.x,d.x)<min(a.x,b.x))return false;
    if (max(c.y,d.y)<min(a.y,b.y))return false;
    if (mult(c, b, a)*mult(b, d, a)<)return false;
    if (mult(a, d, c)*mult(d, b, c)<)return false;
    return true;
}

非规范相交模板（可以理解为重合）

const double eps = 1e-;
double cross(Point a,Point b,Point c){
    return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
}
int dblcmp(double m) {
    if (fabs(m) < eps) return ;
    return m >  ?  : -;
}
bool isCross(Point a,Point b,Point c,Point d){
     if (dblcmp(max(a.x, b.x)-min(c.x, d.x)) >=  && dblcmp(max(c.x, d.x)-min(a.x, b.x)) >=
        && dblcmp(max(a.y, b.y)-min(c.y, d.y)) >=  && dblcmp(max(c.y, d.y)-min(a.y, b.y)) >=
        && dblcmp(cross(a, d, c)*cross(b, d, c)) <=  && dblcmp(cross(c, b, a)*cross(d, b, a)) <= )
                return true;
    return false;
}

题目很坑，有可能输入的不是左上角和右下角...
判断很简单，就是四条边都拿过去判断一下..然后判断一下线段是不是在矩形内。

///判断线段与矩形是否相交
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const double eps = 1e-;
struct Point{
    double x,y;
};
struct Line{
    Point a,b;
}line[];
double cross(Point a,Point b,Point c){
    return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y);
}
int dblcmp(double m) {
    if (fabs(m) < eps) return ;
    return m >  ?  : -;
}
bool isCross(Point a,Point b,Point c,Point d){
     if (dblcmp(max(a.x, b.x)-min(c.x, d.x)) >=  && dblcmp(max(c.x, d.x)-min(a.x, b.x)) >=
        && dblcmp(max(a.y, b.y)-min(c.y, d.y)) >=  && dblcmp(max(c.y, d.y)-min(a.y, b.y)) >=
        && dblcmp(cross(a, d, c)*cross(b, d, c)) <=  && dblcmp(cross(c, b, a)*cross(d, b, a)) <= )
                return true;
    return false;
}
int main()
{
    int tcase;
    scanf("%d",&tcase);
    while(tcase--){
        Line l;
        double lx,ly,rx,ry;
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&l.a.x,&l.a.y,&l.b.x,&l.b.y,&lx,&ly,&rx,&ry);
        if(lx>rx) swap(lx,rx);
        if(ly<ry) swap(ly,ry);
        line[].a.x = lx,line[].a.y =ly,line[].b.x = rx,line[].b.y=ly;
        line[].a.x = lx,line[].a.y =ly,line[].b.x = lx,line[].b.y=ry;
        line[].a.x = lx,line[].a.y =ry,line[].b.x = rx,line[].b.y=ry;
        line[].a.x = rx,line[].a.y =ly,line[].b.x = rx,line[].b.y=ry;
        int flag = false;
        for(int i=;i<=;i++){
            if(isCross(l.a,l.b,line[i].a,line[i].b)){
                flag = true;
                break;
            }
        }
        if(max(l.a.x,l.b.x)<rx&&min(l.a.x,l.b.x)>lx&&max(l.a.y,l.b.y)<ly&&min(l.a.y,l.b.y)>ry) flag = true;
        if(flag) printf("T\n");
        else printf("F\n");
    }
    return ;
}