poj 1066 Treasure Hunt 线段相交

题目链接

题目描述

一个正方形房间被分成若干个小室，宝藏在其中某一点。现可炸开任意一堵墙壁的中点位置。问至少要炸开多少堵墙才能从外面到达宝藏所在地。

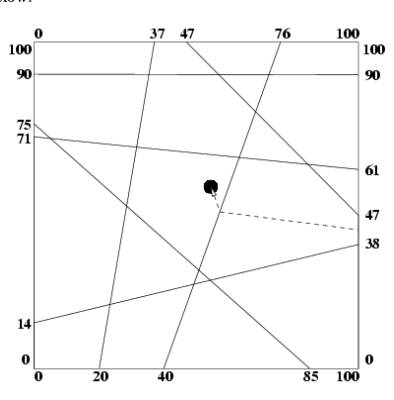
思路

（很巧妙，没想到）

直接枚举墙壁与正方形外壁的交点，与宝藏所在地连线，看连线与多少堵墙相交，即需要炸开的墙壁数目。

为什么呢？因为每堵墙的两个端点都在正方形外壁上，所以宝藏与目的地的连线所经过的墙都是无法绕过去的，必须得炸开。

注意特判没有墙的情况。

Code

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#define inf 0x3f3f3f3f
#define eps 1e-6
#define maxn 110
using namespace std;
typedef long long LL;
struct POINT {
    double x;
    double y;
    POINT(double a=0, double b=0) { x=a; y=b;} //constructor
};
struct LINESEG {
    POINT s;
    POINT e;
    LINESEG(POINT a, POINT b) { s=a; e=b;}
    LINESEG() { }
}seg[maxn];
double multiply(POINT sp,POINT ep,POINT op) {
    return((sp.x-op.x)*(ep.y-op.y)-(ep.x-op.x)*(sp.y-op.y));
}
bool intersect(LINESEG u,LINESEG v) {
    return( (max(u.s.x,u.e.x)>=min(v.s.x,v.e.x))&&                     //排斥实验
        (max(v.s.x,v.e.x)>=min(u.s.x,u.e.x))&&
        (max(u.s.y,u.e.y)>=min(v.s.y,v.e.y))&&
        (max(v.s.y,v.e.y)>=min(u.s.y,u.e.y))&&
        (multiply(v.s,u.e,u.s)*multiply(u.e,v.e,u.s)>=0)&&         //跨立实验
        (multiply(u.s,v.e,v.s)*multiply(v.e,u.e,v.s)>=0));
}
int n;
int calc(LINESEG l) {
    int ret = 0;
    for (int i = 0; i < n; ++i) {
        if (intersect(l, seg[i])) ++ret;
    }
    return ret;
}
void work() {
    for (int i = 0; i < n; ++i) {
        double x1, y1, x2, y2;
        scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
        seg[i] = LINESEG(POINT(x1, y1), POINT(x2, y2));
    }
    POINT p;
    scanf("%lf%lf", &p.x, &p.y);
    if (!n) { printf("Number of doors = 1\n"); return; }
    int ans = inf;
    for (int i = 0; i < n; ++i) {
        ans = min(ans, min(calc(LINESEG(p, seg[i].s)), calc(LINESEG(p, seg[i].e))));
    }
    printf("Number of doors = %d\n", ans);
}
int main() {
    while (scanf("%d", &n) != EOF) work();
    return 0;
}