决策树算法（ID3）

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
3	Overcast	Hot	High	Weak	Yes
4	Rain	Mild	High	Weak	Yes
5	Rain	Cool	Normal	Weak	Yes
6	Rain	Cool	Normal	Strong	No
7	Overcast	Cool	Normal	Strong	Yes
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
10	Rain	Mild	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes
12	Overcast	Mild	High	Strong	Yes
13	Overcast	Hot	Normal	Weak	Yes
14	Rain	Mild	High	Strong	No

对于上面例子，如何判断是否要去playtennis?

可以采用决策树的方式。

决策树是一种以实例为基础的归纳学习算法。从无序列/无规则的数据中，推导出树形表示的分类判决。

优点：计算量小、显示清晰

缺点：容易过拟合（需要修枝）（譬如，使用day做判决，一一对应虽然很准确，但是不能用在其他地方）、对时间顺序的数据，需要过多预处理工作

ID3算法：

1、对于实例，计算各个属性的信息增益

2、对于信息增益最大的属性P作为根节点，P的各个取值的样本作为子集进行分类

3、对于子集下，若只含有正例或反例，直接得到判决；否则递归调用算法，再次寻找子节点

熵：表示随机变量的不确定性。

条件熵：在一个条件下，随机变量的不确定性。

信息增益：熵 - 条件熵，在一个条件下，信息不确定性减少的程度。

用信息增益最大的属性作为结点，是因为最终去不去打球的不确定性，在获得该属性的结果后，不确定性大大降低。

也就是说，该属性对于打球的选择很重要。

对于解决上述问题，

首先，计算系统熵，PlayTennis

P(No) = 5/14

P(Yes) = 9/14

Entropy(S) = -(9/14)*log(9/14)-(5/14)*log(5/14) = 0.94

然后，计算各个属性的熵。

譬如：Wind

其中，Wind中取值为weak的记录有8条，其中，playtennis的正例6个，负例2个；取值为strong的记录有6条，正例为3个，负例为3个。

Entrogy(weak) = -(6/8)*log(6/8)-(2/8)*log(2/8) = 0.811

Entrogy(strong) = -(3/6)*log(3/6)-(3/6)*log(3/6) = 1.0

对应的信息增益为：

Gain(Wind) = Entropy(S) – (8/14)* Entrogy(weak)-(6/14)* Entrogy(strong) = 0.048

同理，Gain(Humidity = 0.151;Gain(Outlook = 0.247;Gain(Temperature = 0.029

此时，可以得到跟节点为：Outlook

对应点决策树：

Outlook分为三个集合：

Sunny：{1，2，8，9，11}，正例：2、反例：3

Overcast：{3，7，12，13}，正例：4、反例：0

Rain：{4，5，6，10，14}，正例：3、反例：2

至此，可以得到：

Sunny:

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
1	Sunny	Hot	High	Weak	No
2	Sunny	Hot	High	Strong	No
8	Sunny	Mild	High	Weak	No
9	Sunny	Cool	Normal	Weak	Yes
11	Sunny	Mild	Normal	Strong	Yes

Entropy(S) = -(3/5)*log(3/5)-(2/5)*log(2/5) = 0.971

对于Wind，weak时，正例为1，反例为2；Strong时，正例为1，反例为1.

Entrogy(weak) = -(1/3)*log(1/3)-(2/3)*log(2/3) = 0.918

Entrogy(strong) = -(1/2)*log(1/2)-(1/2)*log(1/2) = 1

Gain(Wind) = Entropy(S) – 3/5* Entrogy(weak)-2/5* Entrogy(strong) = 0.0202

同理，Gain(Humidity) = 0.971;Gain(Temperature) = 0.571

此时，可以画出部分决策树：

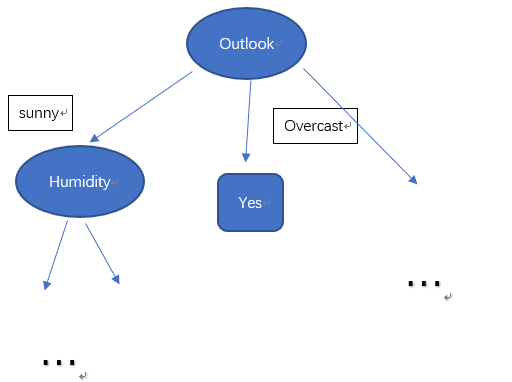
其中，python代码：

import math
#香农公式计算信息熵
def calcShannonEnt(dataset):
    numEntries = len(dataset)
    labelCounts = {}
    for featVec in dataset:
        currentLabel = featVec[-1]#最后一位表示分类
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] +=1

    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*math.log(prob, 2)
    return shannonEnt

def CreateDataSet():
    dataset = [['sunny', 'hot','high','weak', 'no' ],
               ['sunny', 'hot','high','strong', 'no' ],
               ['overcast', 'hot','high','weak', 'yes' ],
               ['rain', 'mild','high','weak', 'yes' ],
               ['rain', 'cool','normal','weak', 'yes' ],
                ['rain', 'cool','normal','strong', 'no' ],
                ['overcast', 'cool','normal','strong', 'yes' ],
                ['sunny', 'mild','high','weak', 'no' ],
                ['sunny', 'cool','normal','weak', 'yes' ],
                ['rain', 'mild','normal','weak', 'yes' ],
                ['sunny', 'mild','normal','strong', 'yes' ],
                ['overcast', 'mild','high','strong', 'yes' ],
                ['overcast', 'hot','normal','weak', 'yes' ],
                ['rain', 'mild','high','strong', 'no' ],
               ]
    labels = ['outlook', 'temperature', 'humidity', 'wind']
    return dataset, labels
#选取属性axis的值value的样本表
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)

    return retDataSet
#选取信息增益最大的属性作为节点
def chooseBestFeatureToSplit(dataSet):
    numberFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numberFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy =0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature
#对于属性已经用完，仍然没有分类的情况，采用投票表决的方法
def majorityCnt(classList):
    classCount ={}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote]=0
        classCount[vote] += 1
    return max(classCount)

def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]
    #类别相同停止划分
    if classList.count(classList[0])==len(classList):
        return classList[0]
    #属性用完，投票表决
    if len(dataSet[0])==1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    return myTree

myDat,labels = CreateDataSet()
tree = createTree(myDat,labels)
print tree

　　

在计算决策树的时候，sklearn库提供了决策树的计算方法（tree），但是，这个库提供的是：

scikit-learn uses an optimised version of the CART algorithm.

对于本文中使用的ID3算法是不支持的。

然而https://pypi.python.org/pypi/decision-tree-id3/0.1.2

该库支持ID3算法。

按照官网说明，注意安装时的依赖库的版本，该升级的升级，该安装的安装即可。‘

from id3 import Id3Estimator
from id3 import export_graphviz

X = [['sunny',    'hot',   'high',   'weak'],
     ['sunny',    'hot',   'high',   'strong'],
     ['overcast', 'hot',   'high',   'weak'],
     ['rain',     'mild',  'high',   'weak'],
     ['rain',     'cool',  'normal', 'weak'],
     ['rain',     'cool',  'normal', 'strong'],
     ['overcast', 'cool',  'normal', 'strong'],
     ['sunny',    'mild',  'high',   'weak'],
     ['sunny',    'cool',  'normal', 'weak'],
     ['rain',     'mild',  'normal', 'weak'],
     ['sunny',    'mild',  'normal', 'strong'],
     ['overcast', 'mild',  'high',   'strong'],
     ['overcast', 'hot',   'normal', 'weak'],
     ['rain',     'mild',  'high',   'strong'],
]
Y = ['no','no','yes','yes','yes','no','yes','no','yes','yes','yes','yes','yes','no']
f = ['outlook','temperature','humidity','wind']
estimator = Id3Estimator()
estimator.fit(X, Y,check_input=True)
export_graphviz(estimator.tree_, 'tree.dot', f)

　　然后通过GraphViz工具生成PDF

dot -Tpdf tree.dot -o tree.pdf

　　结果：

当然，你也可以进行预测判断：

print estimator.predict([['rain',     'mild',  'high',   'strong']])