Splay算法摘要

先介绍变量定义

 int n;
 struct Node {                                                                                        //Splay节点定义
     int fa,son[],val,num,siz;                                                                        //fa:它爸爸；son它儿子，左0右1；val：这个节点的值
                                                                                                     //num：这个值的数量；siz：以它为根的子树的大小
     void res() {                                                                                    //重置节点，用于删除
         fa=son[]=son[]=val=num=siz=;
     }
 } tree[N];
 int ins;
 int root;
 int mem[N],inm;                                                                                    //内存回收池（其实并没有什么用） 

var

判断一个节点是它爸爸的左儿子还是右儿子

这个很简单，比较一下它的值和它爸爸的值就行了

 char ison(int x) {                                                                                    //快速判断一个节点是它爸爸的左儿子（0）还是右儿子 （1）
     return x==tree[tree[x].fa].son[];
 }

ison

Splay的旋转

旋转分为两种主要情况，一种是操作目标的爸爸是根，一种是操作目标的爷爷是根。

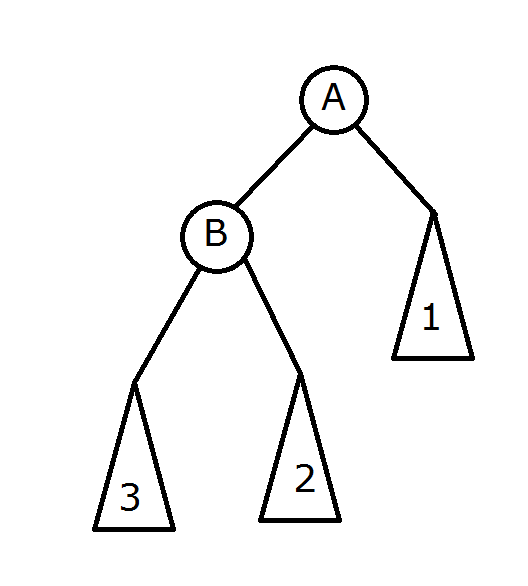如图所示，此时B为A的左儿子，要将B旋转到根。可知A,B,1,2,3的大小关系为3<B<2<A<1。所以旋转后2变成A的左子树（如图）。

同理，B为A的右儿子，则3<A<2<B<1。所以旋转后2为A的右儿子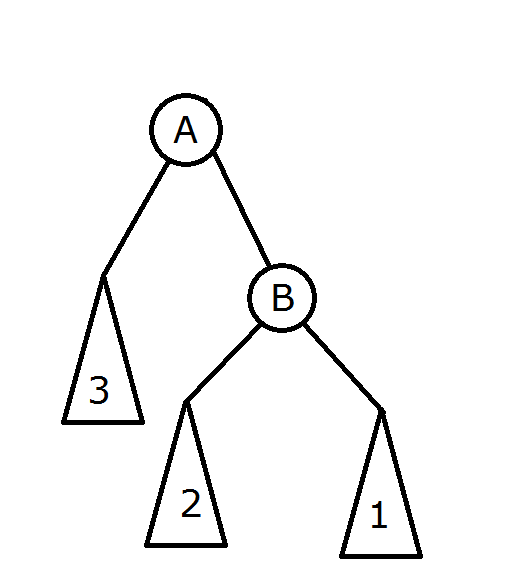

至于另外一种情况自己推一下就好啦

只是有一点，当目标它爸不是根的时候要双旋，具体为：它和它爸同为左儿子或右儿子，则先转它爸再转它；否则转它两次

事实上，这些旋转都是将一个点旋转至它的祖先位置，因此统称为上旋rotate，实现时多为单旋

OIer们耳熟能详的Splay操作其实是多次rotate，实现时一般多为双旋

 void rotate(int x) {                                                                                //上旋（即左旋和右旋）
     int f=tree[x].fa;
     int ff=tree[f].fa;
     int lor=ison(x);
     tree[ff].son[ison(f)]=x;
     tree[x].fa=ff;
     tree[f].son[lor]=tree[x].son[lor^];
     tree[tree[x].son[lor^]].fa=f;
     tree[x].son[lor^]=f;
     tree[f].fa=x;
     tree[f].siz=tree[f].num+tree[tree[f].son[]].siz+tree[tree[f].son[]].siz;
     tree[x].siz=tree[x].num+tree[tree[x].son[]].siz+tree[tree[x].son[]].siz;
 }
 void splay(int x,int goal) {                                                                        //Splay操作,将节点xSplay至节点goal的儿子（若goal为0则Splay至根）
     while(tree[x].fa!=goal) {
         int f=tree[x].fa,ff=tree[f].fa;
         if(!f||!ff)break;
         if(ff!=goal) ison(f)^ison(x)?rotate(x):rotate(f);
         rotate(x);
     }
     if(!goal&&tree[x].fa&&!tree[tree[x].fa].fa)rotate(x);
     if(goal==)root=x;
 }

rotate和Splay

插入

和其他平衡树一样插入就行了，就是最后的时候将其Splay到根

 void insert(int x) {                                                                                //插入一个节点并Splay到根
     int u=root,f=;
     for(; u&&tree[u].val!=x; tree[u].siz++,f=u,u=tree[u].son[x>tree[u].val]);
     if(u) tree[u].num++,tree[u].siz++;
     else {
         if(inm)u=mem[inm--];
         else u=++ins;
         if(f)tree[f].son[x>tree[f].val]=u;
         tree[u].fa=f;
         tree[u].val=x;
         tree[u].num=tree[u].siz=;
     }
     splay(u,);
 }

insert

查找一个数的排名

和其他平衡树一样查找，并将其Splay至根。输出时输出它的左子树的大小+1

 void find(int x) {                                                                                    //查询一个数并Splay到根
     int u=root;
     if(!u)return;
     for(; tree[u].son[x>tree[u].val]&&x!=tree[u].val; u=tree[u].son[x>tree[u].val]);
     splay(u,);
 }

find

查找排名为x的数

和其他平衡树一样查找，并将其Splay至根

void finran(int x) {                                                                                //查询排名为x的数并Splay到根
    int u=root;
    if(!u)return;
    for(char t; tree[u].son[tree[tree[u].son[]].siz+tree[u].num<x?:]&&(tree[tree[u].son[]].siz>=x||tree[tree[u].son[]].siz+tree[u].num<x);
            t=tree[tree[u].son[]].siz+tree[u].num<x,x-=t*(tree[tree[u].son[]].siz+tree[u].num),u=tree[u].son[t]);
    splay(u,);
}

findran

查找一个数的前驱（后继）

这个简单，先找到这个数并将其Splay至根，然后沿它的左儿子（前驱）/右儿子（后继）不断找右儿子（前驱）/左儿子（后继）直至没有儿子

 int nex(int x,int op) {                                                                                //查询一个数的前驱（0）或后继（1）
     find(x);
     int u=root;
     if(tree[u].val>x&&op||tree[u].val<x&&!op||!tree[u].son[op])return u;
     u=tree[u].son[op];
     while(tree[u].son[op^])u=tree[u].son[op^];
     return u;
 }

nex

删除一个数x

首先找到x的前驱和后继，并将前驱Splay至根，后继Splay至前驱的右儿子。由于x的前驱<x<x的后继，易证此时x为后继的左儿子且以它为根的子树大小就是x的个数，直接将其数量减一（x的数量不是1）或将其重置放入内存回收池并将后继的左儿子设为0（x只有1个）。

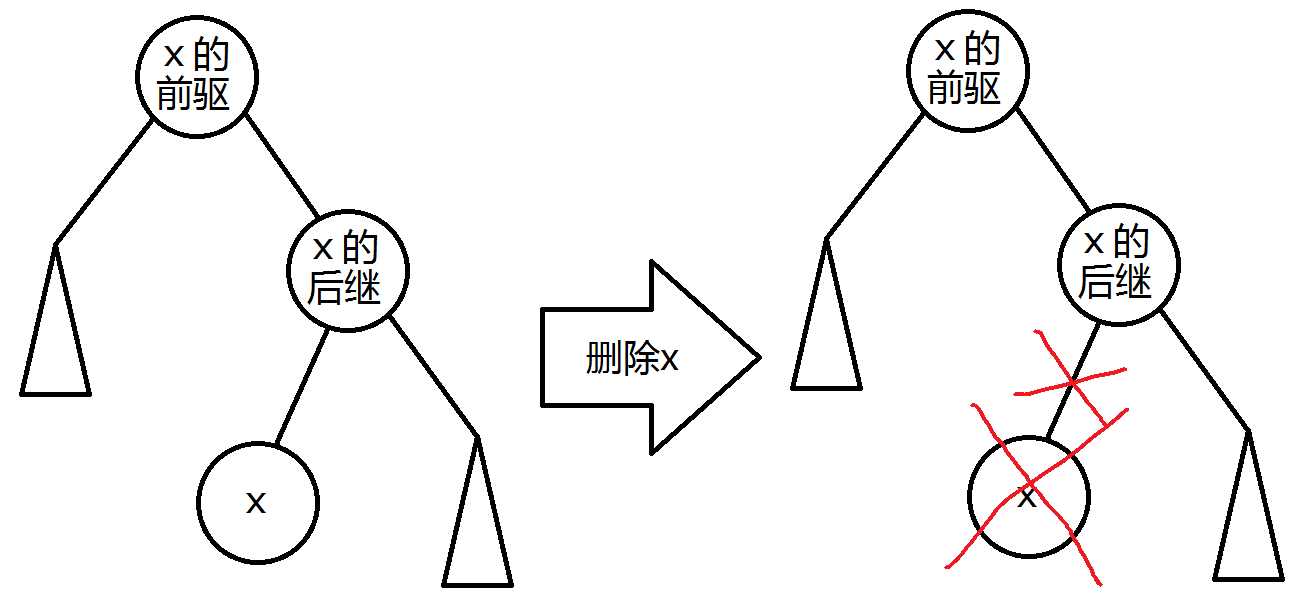
 inline void delet(int x) {                                                                            //删除一个节点
     int la=nex(x,);
     int ne=nex(x,);
     splay(la,);
     if(tree[la].val==x) {
         if(tree[la].num>) {
             --tree[la].num;
             --tree[la].siz;
             return;
         }
         root=tree[la].son[];
         tree[root].fa=;
         mem[++inm]=la;
         tree[la].res();
         return;
     }
     if(tree[ne].val==x) {
         splay(ne,);
         if(tree[ne].num>) {
             --tree[ne].num;
             --tree[ne].siz;
             return;
         }
         root=tree[ne].son[];
         tree[root].fa=;
         mem[++inm]=ne;
         tree[ne].res();
         return;
     }
     splay(ne,la);
     --tree[la].siz;
     --tree[ne].siz;
     int del=tree[ne].son[];
     if(tree[del].num>) {
         tree[del].num--;
         --tree[del].siz;
         splay(del,);
     } else {
         mem[++inm]=tree[ne].son[];
         tree[del].res();
         tree[ne].son[]=;
     }
 }

delet

时空复杂度

时间复杂度

splay：由于树高为均摊logn，因此复杂度为均摊O(logn)

插入、删除、查询：基于splay，因此均摊O(logn)

但常数巨大！！！

常数巨大！！！

常数巨大！！！

空间复杂度

O(n)

例题

洛谷P3369【模板】普通平衡树

 #include<bits/stdc++.h>
 using namespace std;
 #define INF 0x7fffffff
 #define ME 0x7f
 #define FO(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout)
 #define fui(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
 #define fdi(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
 #define fel(i,a) for(register int i=h[a];i;i=ne[i])
 #define ll long long
 #define MEM(a,b) memset(a,b,sizeof(a))
 const int N=;
 int n;struct Node{int fa,son[],val,num,siz;void res(){fa=son[]=son[]=val=num=siz=;}}tree[N];int ins;int root;int mem[N],inm;
 template<class T>
 inline T read(T &n){
     n=;int t=;double x=;char ch;
     for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());(ch=='-')?t=-:n=ch-'';
     for(ch=getchar();isdigit(ch);ch=getchar()) n=n*+ch-'';
     if(ch=='.') for(ch=getchar();isdigit(ch);ch=getchar()) n+=(ch-'')/x,x*=;
     return (n*=t);
 }char ison(int x){return x==tree[tree[x].fa].son[];}
 void rotate(int x){
     int f=tree[x].fa;int ff=tree[f].fa;int lor=ison(x);tree[ff].son[ison(f)]=x;tree[x].fa=ff;tree[f].son[lor]=tree[x].son[lor^];tree[tree[x].son[lor^]].fa=f;tree[x].son[lor^]=f;
     tree[f].fa=x;tree[f].siz=tree[f].num+tree[tree[f].son[]].siz+tree[tree[f].son[]].siz;tree[x].siz=tree[x].num+tree[tree[x].son[]].siz+tree[tree[x].son[]].siz;
 }void splay(int x,int goal){while(tree[x].fa!=goal){int f=tree[x].fa,ff=tree[f].fa;if(!f||!ff)break;if(ff!=goal) ison(f)^ison(x)?rotate(x):rotate(f);rotate(x);}
     if(!goal&&tree[x].fa&&!tree[tree[x].fa].fa)rotate(x);if(goal==)root=x;}
 void find(int x){int u=root;if(!u)return;for(;tree[u].son[x>tree[u].val]&&x!=tree[u].val;u=tree[u].son[x>tree[u].val]);splay(u,);}
 void finran(int x){int u=root;if(!u)return;for(char t;tree[u].son[tree[tree[u].son[]].siz+tree[u].num<x?:]&&(tree[tree[u].son[]].siz>=x||tree[tree[u].son[]].siz+tree[u].num<x);
     t=tree[tree[u].son[]].siz+tree[u].num<x,x-=t*(tree[tree[u].son[]].siz+tree[u].num),u=tree[u].son[t]);splay(u,);
 }void insert(int x){
     int u=root,f=;for(;u&&tree[u].val!=x;tree[u].siz++,f=u,u=tree[u].son[x>tree[u].val]);if(u) tree[u].num++,tree[u].siz++;
     else{if(inm)u=mem[inm--];else u=++ins;if(f)tree[f].son[x>tree[f].val]=u;tree[u].fa=f;tree[u].val=x;tree[u].num=tree[u].siz=;}splay(u,);
 }int nex(int x,int op){find(x);int u=root;if(tree[u].val>x&&op||tree[u].val<x&&!op||!tree[u].son[op])return u;u=tree[u].son[op];while(tree[u].son[op^])u=tree[u].son[op^];return u;}
 inline void delet(int x){
     int la=nex(x,);int ne=nex(x,);splay(la,);if(tree[la].val==x){if(tree[la].num>){--tree[la].num;--tree[la].siz;return;}root=tree[la].son[];tree[root].fa=;mem[++inm]=la;tree[la].res();
     return;}if(tree[ne].val==x){splay(ne,);if(tree[ne].num>){--tree[ne].num;--tree[ne].siz;return;}root=tree[ne].son[];tree[root].fa=;mem[++inm]=ne;tree[ne].res();return;}splay(ne,la);
     --tree[la].siz;--tree[ne].siz;int del=tree[ne].son[];if(tree[del].num>){tree[del].num--;--tree[del].siz;splay(del,);}else{mem[++inm]=tree[ne].son[];tree[del].res();tree[ne].son[]=;}
 }
 int main(){
     read(n);
     fui(i,,n,){
         int opt,x;read(opt);read(x);
         switch(opt){
             case :{insert(x);break;}case :{delet(x);break;}case :{find(x);cout<<tree[tree[root].son[]].siz+<<endl;break;}
             case :{finran(x);cout<<tree[root].val<<endl;break;}case :{cout<<tree[nex(x,)].val<<endl;break;}case :{cout<<tree[nex(x,)].val<<endl;}
         }
     }return ;
 }

AC代码

补充:区间操作

将每个节点的权值改为下标，另建变量存原权值

 

大概就是这些了

哦对了，现实中好像除了LCT就很少用到Splay了

PS:不要信所谓单旋spaly的邪，那只是某大神为了嘲讽人编出来的！！！