神经网络与机器学习 笔记—单神经元解决XOR问题

单神经元解决XOR问题

有两个输入的单个神经元的使用得到的决策边界是输入空间的一条直线。在这条直线的一边的所有的点，神经元输出1；而在这条直线的另一边的点，神经元输出0。在输入空间中，这条直线的位置和方向有两个输入节点相连的神经元的突触权值和它的偏置决定。由于输入模式（0,0）和（1,1）是位于单位正方形相对的两个角，输入模式（0,1）和（1,0）也一样，很明显不能做出这样一条直线作为决策边界可以使（0,0）和（1,1）在一个区域而（0,1）和（1,0）在另一个区域。换句话说，通常一个基本单层感知器不能解决XOR问题，也就是说原始Rosenblatt感知器不能解决XOR问题，所以可以采用多层感知器通过隐藏层来进行维度分块来解决XOR问题。

下面是构造的一个使用一层有两个神经元的隐藏层来解决异或问题，假设

每个神经元都由一个McCulloch-Pitts模型表示，使用阈值函数作为他的激活函数。

比特符号0和1分别有水平0和+1表示。

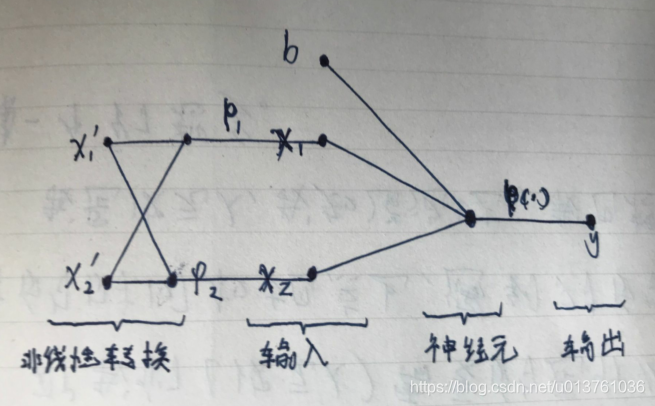
网络结构和信号流图如下：

其中神经元1，神经元2，和神经元1 2共同构造的边界如下图：

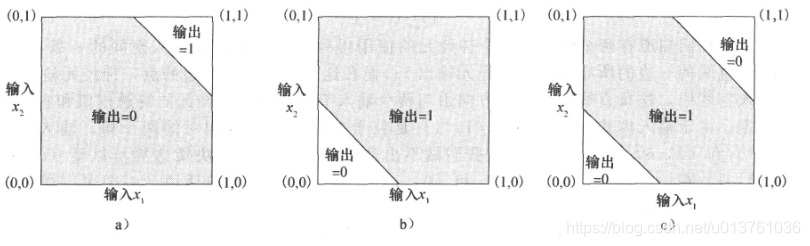
第二种方式是采用非线性映射（高斯函数）解决线性映射模式不可分问题（不增加空间维度）。同时依然保持单个神经元的网络结构。

要求建立一个模式分类产生二值输出相应，（1,1）（0，0）->0 （1,0）（0,1）->1，因此在此输入空间中依Hamming距离最近的点映射到输出空间中最大分离的区域，一个序列的Hamming距离定义为二值序列中从符号1变为符号0的个数，反之亦然。因此，11和00的Hamming距离是0,01和10的Hamming距离是1。

定义一对高斯函数如下：

结果如下：

Tip:cover定理：

将低维线性不可分问题，非线性的投射到高维（甚至同维）空间，使其更容易线性可分（这个以后细说）。