算法 A-Star(A星)寻路

一.简介

在游戏中，有一个很常见地需求，就是要让一个角色从A点走向B点，我们期望是让角色走最少的路。嗯，大家可能会说，直线就是最短的。没错，但大多数时候，A到B中间都会出现一些角色无法穿越的东西，比如墙、坑等障碍物。这个时候怎么办呢？ 是的，我们需要有一个算法来解决这个问题，算法的目标就是计算出两点之间的最短路径，而且要能避开障碍物。

百度百科：

A*搜寻算法俗称A星算法。这是一种在图形平面上，有多个节点的路径，求出最低通过成本的算法。常用于游戏中的NPC的移动计算，或线上游戏的BOT的移动计算上。

二.简化搜索区域

要实现寻路，第一步我们要把场景简化出一个易于控制的搜索区域。

怎么处理要根据游戏来决定了。例如，我们可以将搜索区域划分成像素点，但是这样的划分粒度对于一般的游戏来说太高了（没必要）。

作为代替，我们使用格子（一个正方形）作为寻路算法的单元。其他的形状类型也是可能的（比如三角形或者六边形），但是正方形是最简单并且最常用的。

比如地图的长是w=2000像索，宽是h=2000像索，那么我们这个搜索区域可以是二维数组 map[w, h], 包含有400000个正方形，这实在太多了，而且很多时候地图还会更大。

现在让我们基于目前的区域，把区域划分成多个格子来代表搜索空间（在这个简单的例子中，20*20个格子 = 400 个格子， 每个格式代表了100像索）：

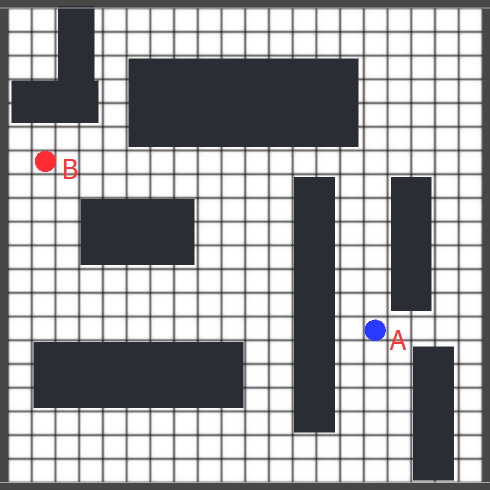
既然我们创建了一个简单的搜索区域，我们来讨论下A星算法的工作原理吧。

我们需要两个列表 (Open和Closed列表)：

一个记录下所有被考虑来寻找最短路径的格子（称为open 列表）

一个记录下不会再被考虑的格子（成为closed列表）

首先在closed列表中添加当前位置（我们把这个开始点称为点 “A”）。然后，把所有与它当前位置相邻的可通行格子添加到open列表中。

现在我们要从A出发到B点。

在寻路过程中，角色总是不停从一个格子移动到另一个相邻的格子，如果单纯从距离上讲，移动到与自身斜对角的格子走的距离要长一些，而移动到与自身水平或垂直方面平行的格子，则要近一些。

为了描述这种区别，先引入二个概念：

节点(Node)：每个格子都可以称为节点。

代价(Cost)：描述角色移动到某个节点时所走的距离（或难易程度）。

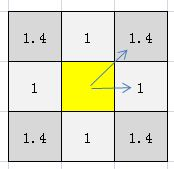
如上图，如果每水平或垂直方向移动相邻一个节点所花的代价记为1，则相邻对角节点的代码为1.4(即2的平方根--勾股定理)

通常寻路过程中的代价用f,g,h来表示

g代表(从指定节点到相邻)节点本身的代价--即上图中的1或1.4

h代表从指定节点到目标节点（根据不同的估价公式--后面会解释估价公式）估算出来的代价。

而 f = g + h 表示节点的总代价

    /// <summary>
    /// 寻路节点
    /// </summary>
    public class NodeItem {
        // 是否是障碍物
        public bool isWall;
        // 位置
        public Vector3 pos;
        // 格子坐标
        public int x, y;

        // 与起点的长度
        public int gCost;
        // 与目标点的长度
        public int hCost;

        // 总的路径长度
        public int fCost {
            get {return gCost + hCost; }
        }

        // 父节点
        public NodeItem parent;

        public NodeItem(bool isWall, Vector3 pos, int x, int y) {
            this.isWall = isWall;
            this.pos = pos;
            this.x = x;
            this.y = y;
        }
    }

注意：这里有二个新的东东 isWall 和 parent。

通常障碍物本身也可以看成是由若干个不可通过的节点所组成，所以 isWall 是用来标记该节点是否为障碍物(节点)。

另外：在考查从一个节点移动到另一个节点时，总是拿自身节点周围的8个相邻节点来说事儿，相对于周边的节点来讲，自身节点称为它们的父节点(parent).

前面一直在提“网格，网格”，干脆把它也封装成类Grid.cs

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

public class Grid : MonoBehaviour {
    public GameObject NodeWall;
    public GameObject Node;

    // 节点半径
    public float NodeRadius = 0.5f;
    // 过滤墙体所在的层
    public LayerMask WhatLayer;

    // 玩家
    public Transform player;
    // 目标
    public Transform destPos;

    /// <summary>
    /// 寻路节点
    /// </summary>
    public class NodeItem {
        // 是否是障碍物
        public bool isWall;
        // 位置
        public Vector3 pos;
        // 格子坐标
        public int x, y;

        // 与起点的长度
        public int gCost;
        // 与目标点的长度
        public int hCost;

        // 总的路径长度
        public int fCost {
            get {return gCost + hCost; }
        }

        // 父节点
        public NodeItem parent;

        public NodeItem(bool isWall, Vector3 pos, int x, int y) {
            this.isWall = isWall;
            this.pos = pos;
            this.x = x;
            this.y = y;
        }
    }

    private NodeItem[,] grid;
    private int w, h;

    private GameObject WallRange, PathRange;
    private List<GameObject> pathObj = new List<GameObject> ();

    void Awake() {
        // 初始化格子
        w = Mathf.RoundToInt(transform.localScale.x * 2);
        h = Mathf.RoundToInt(transform.localScale.y * 2);
        grid = new NodeItem[w, h];

        WallRange = new GameObject ("WallRange");
        PathRange = new GameObject ("PathRange");

        // 将墙的信息写入格子中
        for (int x = 0; x < w; x++) {
            for (int y = 0; y < h; y++) {
                Vector3 pos = new Vector3 (x*0.5f, y*0.5f, -0.25f);
                // 通过节点中心发射圆形射线，检测当前位置是否可以行走
                bool isWall = Physics.CheckSphere (pos, NodeRadius, WhatLayer);
                // 构建一个节点
                grid[x, y] = new NodeItem (isWall, pos, x, y);
                // 如果是墙体，则画出不可行走的区域
                if (isWall) {
                    GameObject obj = GameObject.Instantiate (NodeWall, pos, Quaternion.identity) as GameObject;
                    obj.transform.SetParent (WallRange.transform);
                }
            }
        }

    }

    // 根据坐标获得一个节点
    public NodeItem getItem(Vector3 position) {
        int x = Mathf.RoundToInt (position.x) * 2;
        int y = Mathf.RoundToInt (position.y) * 2;
        x = Mathf.Clamp (x, 0, w - 1);
        y = Mathf.Clamp (y, 0, h - 1);
        return grid [x, y];
    }

    // 取得周围的节点
    public List<NodeItem> getNeibourhood(NodeItem node) {
        List<NodeItem> list = new List<NodeItem> ();
        for (int i = -1; i <= 1; i++) {
            for (int j = -1; j <= 1; j++) {
                // 如果是自己，则跳过
                if (i == 0 && j == 0)
                    continue;
                int x = node.x + i;
                int y = node.y + j;
                // 判断是否越界，如果没有，加到列表中
                if (x < w && x >= 0 && y < h && y >= 0)
                    list.Add (grid [x, y]);
            }
        }
        return list;
    }

    // 更新路径
    public void updatePath(List<NodeItem> lines) {
        int curListSize = pathObj.Count;
        for (int i = 0, max = lines.Count; i < max; i++) {
            if (i < curListSize) {
                pathObj [i].transform.position = lines [i].pos;
                pathObj [i].SetActive (true);
            } else {
                GameObject obj = GameObject.Instantiate (Node, lines [i].pos, Quaternion.identity) as GameObject;
                obj.transform.SetParent (PathRange.transform);
                pathObj.Add (obj);
            }
        }
        for (int i = lines.Count; i < curListSize; i++) {
            pathObj [i].SetActive (false);
        }
    }
}

在寻路的过程中“条条道路通罗马”，路径通常不止一条，只不过所花的代价不同而已。

所以我们要做的事情，就是要尽最大努力找一条代价最小的路径。

但是，即使是代价相同的最佳路径，也有可能出现不同的走法。

用代码如何估算起点与终点之间的代价呢？

//曼哈顿估价法
private function manhattan(node:Node):Number
{
    return Math.abs(node.x - _endNode.x) * _straightCost + Math.abs(node.y + _endNode.y) * _straightCost;
}

//几何估价法
private function euclidian(node:Node):Number
{
    var dx:Number=node.x - _endNode.x;
    var dy:Number=node.y - _endNode.y;
    return Math.sqrt(dx * dx + dy * dy) * _straightCost;
}

//对角线估价法
private function diagonal(node:Node):Number
{
    var dx:Number=Math.abs(node.x - _endNode.x);
    var dy:Number=Math.abs(node.y - _endNode.y);
    var diag:Number=Math.min(dx, dy);
    var straight:Number=dx + dy;
    return _diagCost * diag + _straightCost * (straight - 2 * diag);
}

上面的代码给出了三种基本的估价算法(也称估价公式)，其算法示意图如下：

如上图，对于“曼哈顿算法”最贴切的描述莫过于孙燕姿唱过的那首成名曲“直来直往”，笔直的走，然后转个弯，再笔直的继续。

“几何算法”的最好解释就是“勾股定理”，算出起点与终点之间的直线距离，然后乘上代价因子。

“对角算法”综合了以上二种算法，先按对角线走，一直走到与终点水平或垂直平行后，再笔直的走。

这三种算法可以实现不同的寻路结果，我们这个例子用的是“对角算法”：

复制代码
    // 获取两个节点之间的距离
    int getDistanceNodes(Grid.NodeItem a, Grid.NodeItem b) {
        int cntX = Mathf.Abs (a.x - b.x);
        int cntY = Mathf.Abs (a.y - b.y);
        // 判断到底是那个轴相差的距离更远 ， 实际上，为了简化计算，我们将代价*10变成了整数。
        if (cntX > cntY) {
            return 14 * cntY + 10 * (cntX - cntY);
        } else {
            return 14 * cntX + 10 * (cntY - cntX);
        }
    }

好吧，下面直接贴出全部的寻路算法 FindPath.cs:

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

public class FindPath : MonoBehaviour {
    private Grid grid;

    // Use this for initialization
    void Start () {
        grid = GetComponent<Grid> ();
    }

    // Update is called once per frame
    void Update () {
        FindingPath (grid.player.position, grid.destPos.position);
    }

    // A*寻路
    void FindingPath(Vector3 s, Vector3 e) {
        Grid.NodeItem startNode = grid.getItem (s);
        Grid.NodeItem endNode = grid.getItem (e);

        List<Grid.NodeItem> openSet = new List<Grid.NodeItem> ();
        HashSet<Grid.NodeItem> closeSet = new HashSet<Grid.NodeItem> ();
        openSet.Add (startNode);

        while (openSet.Count > 0) {
            Grid.NodeItem curNode = openSet [0];

            for (int i = 0, max = openSet.Count; i < max; i++) {
                if (openSet [i].fCost <= curNode.fCost &&
                    openSet [i].hCost < curNode.hCost) {
                    curNode = openSet [i];
                }
            }

            openSet.Remove (curNode);
            closeSet.Add (curNode);

            // 找到的目标节点
            if (curNode == endNode) {
                generatePath (startNode, endNode);
                return;
            }

            // 判断周围节点，选择一个最优的节点
            foreach (var item in grid.getNeibourhood(curNode)) {
                // 如果是墙或者已经在关闭列表中
                if (item.isWall || closeSet.Contains (item))
                    continue;
                // 计算当前相领节点现开始节点距离
                int newCost = curNode.gCost + getDistanceNodes (curNode, item);
                // 如果距离更小，或者原来不在开始列表中
                if (newCost < item.gCost || !openSet.Contains (item)) {
                    // 更新与开始节点的距离
                    item.gCost = newCost;
                    // 更新与终点的距离
                    item.hCost = getDistanceNodes (item, endNode);
                    // 更新父节点为当前选定的节点
                    item.parent = curNode;
                    // 如果节点是新加入的，将它加入打开列表中
                    if (!openSet.Contains (item)) {
                        openSet.Add (item);
                    }
                }
            }
        }

        generatePath (startNode, null);
    }

    // 生成路径
    void generatePath(Grid.NodeItem startNode, Grid.NodeItem endNode) {
        List<Grid.NodeItem> path = new List<Grid.NodeItem>();
        if (endNode != null) {
            Grid.NodeItem temp = endNode;
            while (temp != startNode) {
                path.Add (temp);
                temp = temp.parent;
            }
            // 反转路径
            path.Reverse ();
        }
        // 更新路径
        grid.updatePath(path);
    }

    // 获取两个节点之间的距离
    int getDistanceNodes(Grid.NodeItem a, Grid.NodeItem b) {
        int cntX = Mathf.Abs (a.x - b.x);
        int cntY = Mathf.Abs (a.y - b.y);
        // 判断到底是那个轴相差的距离更远
        if (cntX > cntY) {
            return 14 * cntY + 10 * (cntX - cntY);
        } else {
            return 14 * cntX + 10 * (cntY - cntX);
        }
    }

}

运行效果图：

红色区域是标识出来的不可以行走区域。

完整代码下载

http://pan.baidu.com/s/1jInjLDs