二叉树Bynary_Tree（2）：二叉树的递归遍历

前言

---

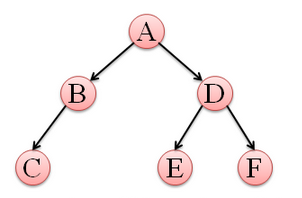
　　以下的代码实现都以该完全二叉树为例：

　　

声明结构体

---

typedef struct node
{
        char ch;
        struct node *lchild;
        struct node *rchild;
}TreeNode,*Tree;  //注意区别，例如TreeNode X1与*Tree X2，X1为结构体变量，X2为结构体指针变量

创建树

---

　　

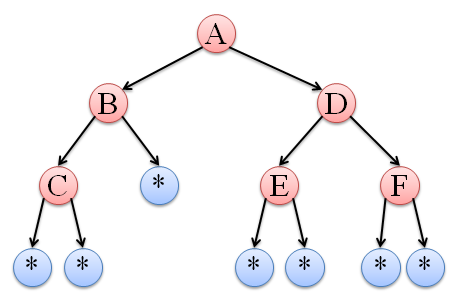
　　1.采用前序创建

　　2.若某子结点为不存在，则将其置为NULL，方法为：判断输入的字符是否为' * '，若为* ，则置当前结点为NULL

　　3.递归创建子结点

void Create_pro(Tree* T)
{
    char ch;
    scanf("%c", &ch);  //需一次性输入所有字符，若分行输入，由于缓冲区问题，多出的空格将一直递归下去
    if (ch == '*')
    {
        *T = NULL;
    }
    else
    {
        *T = (Tree)malloc(sizeof(TreeNode));
        (*T)->ch = ch;
        Create_pro(&((*T)->lchild));
        Create_pro(&((*T)->rchild));
    }
}

　　这里遇到的scanf缓冲区问题可移步：http://bbs.csdn.net/topics/390284350?page=1

删除二叉树

---

void ClearTree(Tree *T)
{
    if (!*T)
    {
        return;
    }  

    ClearTree(&(*T)->lchild);
    ClearTree(&(*T)->rchild);
    free(*T);
    *T = NULL;
}

前（根）序遍历

---

　　先访问根结点，再分别前序遍历左、右两棵子树。前序遍历的结果是：ABCDEF

void Show_pro(Tree t)
{
        if(!t)
                return;
        printf("%c ",t->ch);
        Show_pro(t->lchild);
        Show_pro(t->rchild);
}

中（根）序遍历

---

　　先中序遍历左子树，然后再访问根结点，最后再中序遍历遍历右子树。中序遍历的结果是：CBADEF

void Show_mid(Tree t)
{
        if(!t)
                return;
        Show_mid(t->lchild);
        printf("%c ",t->ch);
        Show_mid(t->rchild);
}

后（根）序遍历

---

　　先后序遍历左子树，然后后序遍历右子树，最后访问根结点。后序遍历的结果是：CBEFDA

void Show_back(Tree t)
{
        if(!t)
                return;
        Show_back(t->lchild);
        Show_back(t->rchild);
        printf("%c ",t->ch);
}

层次遍历

---

　　先按深度划分层，深度为1的对应树的第一层，深度为二的对应树的第二层...以此类推。然后逐层访问结点。

　　除层次遍历外的三种遍历的设计核心思想为栈，后进先出，因此想到递归。而层次遍历是队列，先进先出，我采用循环队列去解决。具体的算法设计如下：

　　　　1.定义一个队列Tree q[MAX]存储队列数据，头变量front与尾变量rear存储首尾位置，规定front == rear时队列为空。

　　　　2.初始化，令 front = 0 ，rear = 0

　　　　3.入队操作。将树T存入q[rear]中，即T入队，然后 rear = (rear+1)%MAX ，保持rear在0到MAX中循环

　　　　4.输出结点数据。同时判断子结点中数据的存在情况，子结点不为NULL，则再进行入队操作

　　　　5.出队操作。front = (front+1)%MAX;

void Show_level(Tree T)
{
        Tree q[MAX];  //队列
        Tree p;  //当前结点
        int front;
        int rear;

        //初始化
        front =0;
        rear =0;

        if(T)
        {
                q[rear] = T;
                rear = (rear+1)%MAX;
        }

        while(front != rear)
        {
                p = q[front];
                printf("%c ",p->ch);
                if(p->lchild)
                {
                        q[rear] = p->lchild;
                        rear = (rear+1)%MAX;
                }
                if(p->rchild)
                {
                        q[rear] = p->rchild;
                        rear = (rear+1)%MAX;
                }
                front = (front+1)%MAX;
        }
}

　　层次遍历模块中有一个难点，即是入队操作，如何将树并入队列呢？我们想到将若根结点并入队列，那么整棵树便并入队列了。然而，就必须考虑一个问题，根结点的地址就是T的地址吗？

　　

　　通过在create_tree时将每一次申请的结点地址打印出来，并在创建完毕后在main函数里printf一次T的地址，实际结果如图，根结点地址果然是T的地址，那么我们就可以用根结点入队来实现整棵树入队的操作了，同时也可得到一个结论：递归建树，根结点地址即是树的地址。

判断树是否为空树

---

void IsTreeEmpty(Tree T)
{
        if(T)
                printf("Tree is not empty\n");
        else
                printf("Tree is empty\n");
}

　　

源代码

---

/*************************************************************************
	> File Name: Binary tree
	> Author: Bw98
	> Mail: 786016746@qq.com
	> Blog: www.cnblogs.com/Bw98blogs/
	> Created Time: SUN 16th Jul. 2017
 ************************************************************************/
#include<stdio.h>
#include<stdlib.h>
#define MAX 100
typedef struct node
{
        char ch;
        struct node *lchild;
        struct node *rchild;
}TreeNode,*Tree;

void InitTree(Tree *T);  //树初始化
void Create_pro(Tree *T);  //创建一棵树并输入相应元素
void Show_pro(Tree t);  //先（根）序遍历输出
void Show_mid(Tree t);  //中（根）序遍历输出
void Show_back(Tree t);  //后（根）序遍历输出
void Show_level(Tree T);  //层次遍历输出
void IsTreeEmpty(Tree T);  //检测树是否为空
void ClearTree(Tree *T);  //清除树

int main()
{
        Tree t;
        InitTree(&t);
        printf("输入前序遍历序列（输入'*'时，该树结点为空）\n");
        Create_pro(&t);
        Show_pro(t);
        Show_mid(t);
        Show_back(t);
        Show_level(t);
        IsTreeEmpty(t);
        ClearTree(&t);
        IsTreeEmpty(t);
        return 0;
}

void InitTree(Tree *T)
{
        *T =NULL;
}

void Create_pro(Tree* T)
{
    char ch;
    scanf("%c", &ch);
    if (ch == '*')
    {
        *T = NULL;
    }
    else
    {
        *T = (Tree)malloc(sizeof(TreeNode));
        (*T)->ch = ch;
        Create_pro(&((*T)->lchild));
        Create_pro(&((*T)->rchild));
    }
}

void Show_pro(Tree t)
{
        if(!t)
                return;
        printf("%c ",t->ch);
        Show_pro(t->lchild);
        Show_pro(t->rchild);
}

void Show_mid(Tree t)
{
        if(!t)
                return;
        Show_mid(t->lchild);
        printf("%c ",t->ch);
        Show_mid(t->rchild);
}

void Show_back(Tree t)
{
        if(!t)
                return;
        Show_back(t->lchild);
        Show_back(t->rchild);
        printf("%c ",t->ch);
}

void Show_level(Tree T)
{
        Tree q[MAX];  //队列
        Tree p;  //当前结点
        int front;
        int rear;

        //初始化
        front =0;
        rear =0;

        if(T)
        {
                q[rear] = T;
                rear = (rear+1)%MAX;
        }

        while(front != rear)
        {
                p = q[front];
                printf("%c ",p->ch);
                if(p->lchild)
                {
                        q[rear] = p->lchild;
                        rear = (rear+1)%MAX;
                }
                if(p->rchild)
                {
                        q[rear] = p->rchild;
                        rear = (rear+1)%MAX;
                }
                front = (front+1)%MAX;
        }
}

void IsTreeEmpty(Tree T)
{
        if(T)
                printf("Tree is not empty\n");
        else
                printf("Tree is empty\n");
}

void ClearTree(Tree *T)
{
    if (!(*T))
    {
        return;
    }

    ClearTree(&(*T)->lchild);
    ClearTree(&(*T)->rchild);
    free(*T);
    *T = NULL;
}