[WikiOI "天梯"1281] Xn数列
题目描述Description
给你6个数,m, a, c, x0, n, g
Xn+1 = ( aXn + c ) mod m,求Xn
m, a, c, x0, n, g<=10^18
输入描述Input Description
一行六个数 m, a, c, x0, n, g
输出描述Output Description
输出一个数 Xn mod g
样例输入Sample Input
11 8 7 1 5 3
样例输出Sample Output
2
数据范围及提示Data Size & Hint
int64按位相乘可以不要用高精度。
题目分析
典型的矩阵快速幂问题。由递推式 Xn+1 = ( aXn + c ) mod m 可以构造出矩阵方程:
那么题目所求就可转化为一个1*2矩阵与n个二阶方阵的矩阵链乘。根据矩阵乘法的结合律,可得出:

即可转化为矩阵快速幂问题。其中的乘法运算已改为了倍增取模乘法。
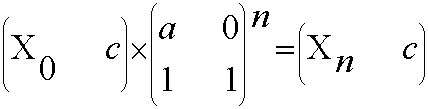
1 //WikiOI 1281 Xn数列
2 #include <iostream>
3 using namespace std;
4 typedef long long LL;
5 LL m, a, c, x0, n, MOD;
6 LL mlti(LL a, LL b) //倍增取模乘法
7 {
8 a %= m;
9 LL ans = ;
while(b)
{
if(b & )ans = (ans + a)% m;
a = (a << )% m;
b >>= ;
}
return ans;
}
struct Matrix2
{
LL val[][];
Matrix2(LL k1,LL k2,LL k3,LL k4)
{
val[][] = k1; val[][] = k2; val[][] = k3; val[][] = k4;
}
void Mlti(Matrix2 &m) //矩阵乘法
{
LL v1 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v2 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v3 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v4 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
val[][] = v1,val[][] = v2,val[][] = v3,val[][] = v4;
}
};
int main()
{
ios::sync_with_stdio(); //感谢陈思学长!
cin >>m >>a >>c >>x0 >>n >>MOD;
Matrix2 M(a, , , );
Matrix2 ans = M;
n -= ;
while(n)
{
if(n & ) ans.Mlti(M);
M.Mlti(M);
n >>=;
}
cout << ((mlti(x0, ans.val[][])+mlti(c, ans.val[][]))%m)%MOD;
return ;
}
那么题目所求就可转化为一个1*2矩阵与n个二阶方阵的矩阵链乘。根据矩阵乘法的结合律,可得出:

即可转化为矩阵快速幂问题。其中的乘法运算已改为了倍增取模乘法。
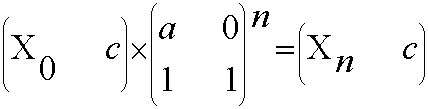
1 //WikiOI 1281 Xn数列
2 #include <iostream>
3 using namespace std;
4 typedef long long LL;
5 LL m, a, c, x0, n, MOD;
6 LL mlti(LL a, LL b) //倍增取模乘法
7 {
8 a %= m;
9 LL ans = ;
while(b)
{
if(b & )ans = (ans + a)% m;
a = (a << )% m;
b >>= ;
}
return ans;
}
struct Matrix2
{
LL val[][];
Matrix2(LL k1,LL k2,LL k3,LL k4)
{
val[][] = k1; val[][] = k2; val[][] = k3; val[][] = k4;
}
void Mlti(Matrix2 &m) //矩阵乘法
{
LL v1 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v2 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v3 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
LL v4 = mlti(val[][],m.val[][])+mlti(val[][],m.val[][]);
val[][] = v1,val[][] = v2,val[][] = v3,val[][] = v4;
}
};
int main()
{
ios::sync_with_stdio(); //感谢陈思学长!
cin >>m >>a >>c >>x0 >>n >>MOD;
Matrix2 M(a, , , );
Matrix2 ans = M;
n -= ;
while(n)
{
if(n & ) ans.Mlti(M);
M.Mlti(M);
n >>=;
}
cout << ((mlti(x0, ans.val[][])+mlti(c, ans.val[][]))%m)%MOD;
return ;
}
[WikiOI "天梯"1281] Xn数列的更多相关文章
- 【wikioi】1281 Xn数列(矩阵乘法)
http://wikioi.com/problem/1281/ 矩阵真是个神奇的东西.. 只要搞出一个矩阵乘法,那么递推式可以完美的用上快速幂,然后使复杂度降到log 真是神奇. 在本题中,应该很快能 ...
- Codevs No.1281 Xn数列
2016-06-01 16:28:25 题目链接: Xn数列 (Codevs No.1281) 题目大意: 给定一种递推式为 Xn=(A*Xn-1+C)%M 的数列,求特定的某一项%G 解法: 矩阵乘 ...
- codevs 1281 Xn数列
题目描述 Description 给你6个数,m, a, c, x0, n, g Xn+1 = ( aXn + c ) mod m,求Xn m, a, c, x0, n, g<=10^18 输入 ...
- 【CODEVS】1281 Xn数列
[算法]矩阵快速幂 [题解]T*A(n-1)=A(n)矩阵如下: a 1 * x(n-1) 0 = xn 0 0 1 c 0 c 0 防止溢出可以用类似快速幂的快速乘. ...
- codevs 1281 Xn数列 (矩阵乘法)
/* 再来个题练练手 scanf longlong 有bug....... */ #include<cstdio> #include<iostream> #include< ...
- C++之路进阶——codevs1281(Xn数列)
1281 Xn数列 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 大师 Master 题目描述 Description 给你6个数,m, a, c, x0, n, ...
- Xn数列(codevs 1281)
题目描述 Description 给你6个数,m, a, c, x0, n, g Xn+1 = ( aXn + c ) mod m,求Xn m, a, c, x0, n, g<=10^18 输入 ...
- 【wikioi】1250 Fibonacci数列(矩阵乘法)
http://wikioi.com/problem/1250/ 我就不说这题有多水了. 0 1 1 1 矩阵快速幂 #include <cstdio> #include <cstri ...
- codevs1281 Xn数列
题目描述 Description 给你6个数,m, a, c, x0, n, g Xn+1 = ( aXn + c ) mod m,求Xn m, a, c, x0, n, g<=10^18 输入 ...
随机推荐
- ie8下input文字偏上select文字偏下
1.ie8下input文字偏上 正常情况下input的显示情况如下 当设置input的高度时,就会出现文字不垂直居中偏上的情况,如图 解决方案 强input的行高line-height与其高度设置一致 ...
- sublime3插件安装及报错处理
ctrl+shift+p调用出窗口:输入install package,然后输入想安装的插件. 有些用户安装的可能是国内破解版的,我的就是,然后install package报错: Package C ...
- Django之项目搭建和配置总结(一)
安装和创建虚拟环境 参考:linux系统下Python虚拟环境的安装和使用 安装Django包 先进入虚拟环境,在联网下执行: pip install django==1.8.7 1.8.7表示dja ...
- .gitignore 文件添加或更新后规则无效的解决方案
项目已经提交之后,突然想忽略某个文件或目录 A,于是在 .gitignore 里添加了忽略规则.但是提交(commit)之后,发现一旦修改了 A,git 同样会检测到 A 的变化(changes) , ...
- 64_k2
kf5-libkdepim-akonadi-17.04.1-1.fc26.x86_64.rpm 25-May-2017 12:22 177198 kf5-libkdepim-devel-17.04.1 ...
- MNIST数据集转化为二维图片
#coding: utf-8 from tensorflow.examples.tutorials.mnist import input_data import scipy.misc import o ...
- Leetcode 之Longest Common Prefix(33)
在一组字符串中找到最长的子串.采用纵向匹配,遇到第一个不匹配的停止. string longestComPrefix(vector<string> &strs) { if (str ...
- Solr产品化部署
1.下载solr-6.4.1.tgz到任意目录 2.执行tar xzf solr-6.4.1.tgz solr-6.4.1/bin/install_solr_service.sh --strip-co ...
- UVA - 796
UVA- 796 /** 题意:给出一个图,然后看此图的存在的桥,并且输出是哪一个, 做法:Tarjan(不存在重边) **/ #include<iostream> #include< ...
- Django 项目CRM总结
0. 项目说明: 1. 销售自动分配客户资源: 给销售分配权重及承单数量,创建权重表,通过销售权重进行从大到小进行排序 以承单数循环添加到列表,承单数是多少列表添加就添加多少次 考虑到如果服务重启,或 ...
