Dynamic Programming | Set 4 (Longest Common Subsequence)

首先来看什么是最长公共子序列：给定两个序列，找到两个序列中均存在的最长公共子序列的长度。子序列需要以相关的顺序呈现，但不必连续。例如，“abc”, “abg”, “bdf”, “aeg”, ‘”acefg”等都是“abcdefg”的子序列。因此，一个长度为n的序列拥有2^n中可能的子序列（序列中的每一个元素只有选或者不选两种可能，因此是2^n）。

Example：

LCS for input Sequences “ABCDGH” and “AEDFHR” is “ADH” of length 3.
LCS for input Sequences “AGGTAB” and “GXTXAYB” is “GTAB” of length 4.

该问题最普通的解法是对两个给定序列分别生成所有子序列，然后找到最长的匹配的子序列。这样的解法是指数复杂度的，显然不是我们需要的。我们来看该问题是如何拥有动态规划问题的重要性质的。

1 Optimal Substructure:

假设输入序列分别为长度为m的X[0..m-1]和长度为n的Y[0..n-1]，令L(X[0..m-1], Y[0..n-1])为序列X、Y的最长公共子序列的长度，如下为L(X[0..m-1], Y[0..n-1])的递归定义：

If last characters of both sequences match (or X[m-1] == Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])

If last characters of both sequences do not match (or X[m-1] != Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2])

例子：

1) Consider the input strings “AGGTAB” and “GXTXAYB”. Last characters match for the strings. So length of LCS can be written as:
L(“AGGTAB”, “GXTXAYB”) = 1 + L(“AGGTA”, “GXTXAY”)

2) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as:
L(“ABCDGH”, “AEDFHR”) = MAX ( L(“ABCDG”, “AEDFHR”), L(“ABCDGH”, “AEDFH”) )

因此，LCS问题具有最优子结构性质，可以使用求解子问题的方案来解决。

2 Overlapping Subproblems:

如下是LCS问题的递归求解程序，该实现遵循了上面的递归结构：

/* A Naive recursive implementation of LCS problem */
#include<stdio.h>
#include<stdlib.h>

int max(int a, int b);

/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
int lcs( char *X, char *Y, int m, int n )
{
   if (m == 0 || n == 0)
     return 0;
   if (X[m-1] == Y[n-1])
     return 1 + lcs(X, Y, m-1, n-1);
   else
     return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
}

/* Utility function to get max of 2 integers */
int max(int a, int b)
{
    return (a > b)? a : b;
}

/* Driver program to test above function */
int main()
{
  char X[] = "AGGTAB";
  char Y[] = "GXTXAYB";

  int m = strlen(X);
  int n = strlen(Y);

  printf("Length of LCS is %d\n", lcs( X, Y, m, n ) );

  getchar();
  return 0;
}

以上程序的时间复杂度在最坏情况下是O(2^n)，最坏情况是X与Y中的所有字符均不匹配，也就是说LCS的长度为0。

根据上面的实现，如下是当输入序列为“AXYT”和“AYZX”时的部分递归树：

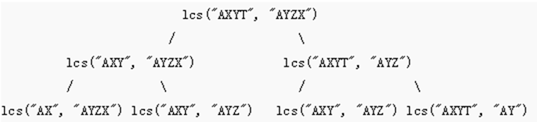
不难发现，lcs(“AXY”, “AYZ”) 被计算了2次。如果我们画出完整的递归树，会找到更多被重复计算的子问题。因此，该问题具备重叠子结构性质，可以通过Memoization或者Tabulation来避免重复计算。下面是LCS问题的Tabulation实现。

/* Dynamic Programming implementation of LCS problem */
#include<stdio.h>
#include<stdlib.h>

int max(int a, int b);

/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
int lcs( char *X, char *Y, int m, int n )
{
   int L[m+1][n+1];
   int i, j;

   /* Following steps build L[m+1][n+1] in bottom up fashion. Note
      that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */
   for (i=0; i<=m; i++)
   {
     for (j=0; j<=n; j++)
     {
       if (i == 0 || j == 0)
         L[i][j] = 0;

       else if (X[i-1] == Y[j-1])
         L[i][j] = L[i-1][j-1] + 1;

       else
         L[i][j] = max(L[i-1][j], L[i][j-1]);
     }
   }

   /* L[m][n] contains length of LCS for X[0..n-1] and Y[0..m-1] */
   return L[m][n];
}

/* Utility function to get max of 2 integers */
int max(int a, int b)
{
    return (a > b)? a : b;
}

/* Driver program to test above function */
int main()
{
  char X[] = "AGGTAB";
  char Y[] = "GXTXAYB";

  int m = strlen(X);
  int n = strlen(Y);

  printf("Length of LCS is %d\n", lcs( X, Y, m, n ) );

  getchar();
  return 0;
}

以上实现的时间复杂度为O(mn)，相比原始递归求解的最坏情况要好太多了。

上面的程序只是返回了LCS的长度，可以参照该文章来打印LCS Printing Longest Common Subsequence 。