近端梯度算法（Proximal Gradient Descent）

L1正则化是一种常用的获取稀疏解的手段，同时L1范数也是L0范数的松弛范数。求解L1正则化问题最常用的手段就是通过加速近端梯度算法来实现的。

考虑一个这样的问题：

　　min_x  f(x)+λg(x)

x∈Rⁿ，f(x)∈R，这里f(x)是一个二阶可微的凸函数，g(x)是一个凸函数（或许不可导），如上面L1的正则化||x||。

此时，只需要f(x)满足利普希茨（Lipschitz）连续条件，即对于定义域内所有向量x,y，存在常数M使得||f'(y)-f'(x)||<=M·||y-x||，那么这个模型就可以通过近端梯度算法来进行求解了。

ps：下面涉及很多数学知识，不想了解数学的朋友请跳到结论处，个人理解，所以也不能保证推理很严谨，如有问题，请一定帮忙我告诉我。

利普希茨连续条件的几何意义可以认为是函数在定义域内任何点的梯度都不超过M（梯度有上限），也就是说不会存在梯度为正负无穷大的情况。

因而，我们有下图所示的推算：

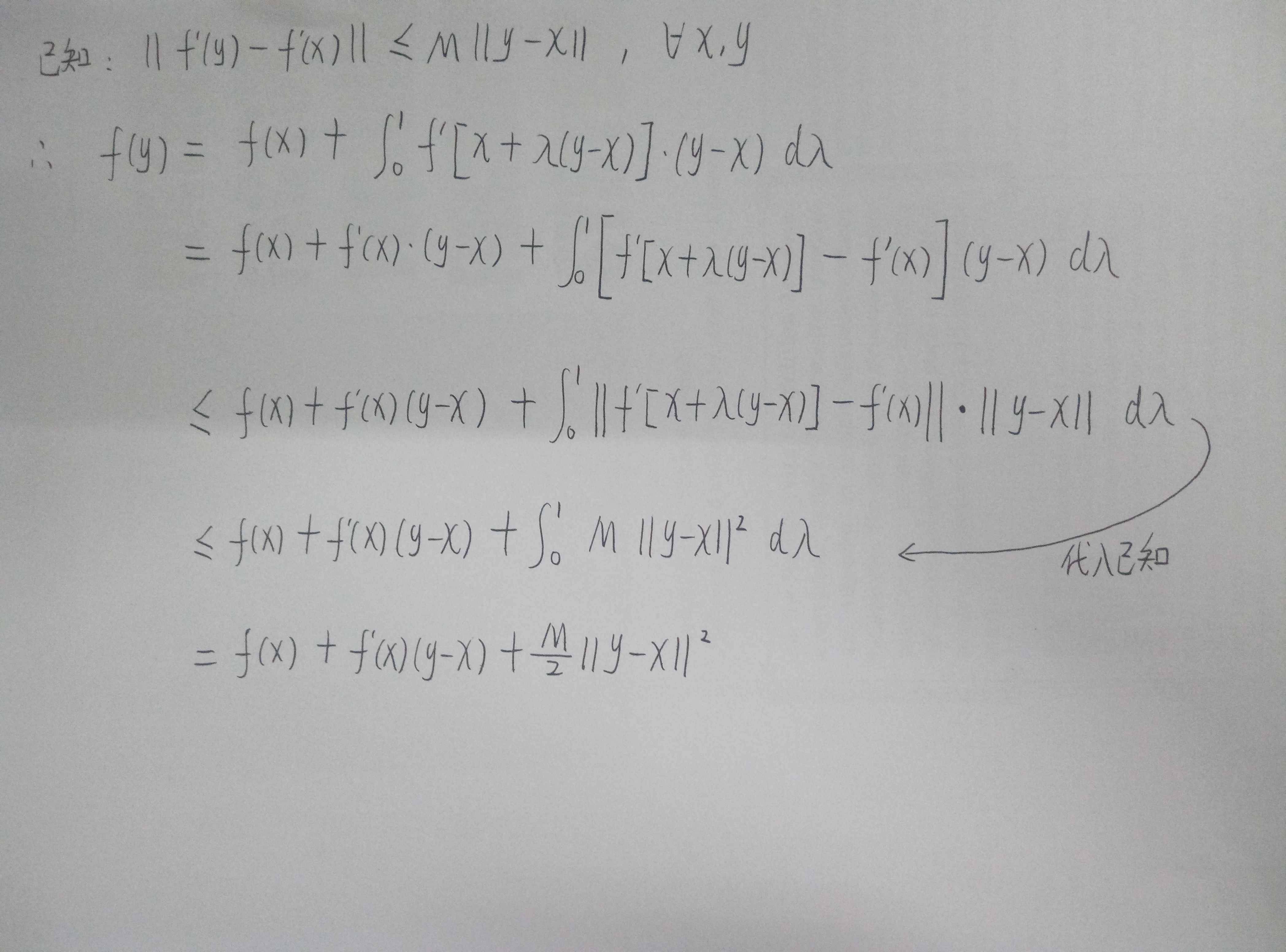
我们可以用f(y) = f(x)+f'(x)(y-x)+M/2*||y-x||²来近似的表示f(y)，也可以认为是高维下的泰勒分解，取到二次项。

我们换一种写法，f(x_k+1) = f(x_k)+f'(x_k)(x_k+1-x_k)+M/2*||x_k+1-x_k||²，也就是说可以直接迭代求min_x f(x)，就是牛顿法辣。

再换一种写法，f(x_k+1)=(M/2)(x_k+1-(x_k+(1/M)f'(x_k)))²+CONST，其中CONST是一个与x_k+1无关的常数，也就是说，此时我们可以直接写出这个条件下x_k+1的最优取值就是x_k+1=x_k+(1/M)f'(x_k)。令z=x_k+(1/M)f'(x_k)。

回到原问题，min_x  f(x)+λg(x)，此时问题变为了求解min_x  (M/2)||x-z||²+λg(x)。

实际上在求解这个问题的过程中，x的每一个维度上的值是互不影响的，可以看成n个独立的一维优化问题进行求解，最后组合成一个向量就行。

如果g(x)=||x||₁，就是L1正则化，那么最后的结论可以通过收缩算子来表示。

即x^k+1=shrink(z,λ/M)。具体来说，就是Z向量的每一个维度向原点方向移动λ/M的距离（收缩，很形象），对于x^k+1的第i个维度x_i=sgn(z_i)*max(|z_i|-λ/M,0)，其中sgn()为符号函数，正数为1，负数为-1。

一直迭代直到x^k收敛吧。

参考文献：

[1]Nesterov Y. Introductory lectures on convex optimization: A basic course[M]. Springer Science & Business Media, 2013.

[2]https://people.eecs.berkeley.edu/~elghaoui/Teaching/EE227A/lecture18.pdf