CF1292C Xenon's Attack on the Gangs 题解

传送门

题目描述

输入格式

输出格式

题意翻译

给n个结点，n-1条无向边。即一棵树。我们需要给这n-1条边赋上0~ n-2不重复的值。mex(u,v)表示从结点u到结点v经过的边权值中没有出现的最小非负整数。计算下面等式的最大值：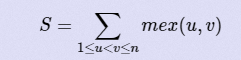

样例

样例输入

样例输入一

样例输入二

样例输出

样例输出一

样例输出二

分析

我们先随便找一条边，将它的价值赋值成0

那么只要有一个路径经过这条边，那么这个路径的最小价值就一定不会为0

我们举一个例子

此时u到v的价值为0，那么这一条路径不经过的最小非负整数就是1

一条路径只要经过(u,v)这条边，那么它们不经过的最小非负整数就至少为1（因为它们已经经过了0）

我们用f[i][j]表示从i开始，从j结束，将i到j之间所有的m条边赋值成0到m-1所得到的最大价值

用g[i][j]表示在i号节点作为根节点的情况下，以j为根节点的子树的大小

用pa[i][j]表示在i号节点作为根节点的情况下，j节点的父亲节点

我们再来看上面这幅图，只要经过（u,v）这条边，那么它们没有经过的最小非负整数的价值就至少为1

此时总价值为g[u][v]*g[v][u]

那么我们再添加价值为1的边，为了使总的价值最大，这条边显然要和价值为0的边放在一起

为什么呢？因为如果放在别的地方，那么价值为1的路程会增多，而价值为2的路程会减少

换一句话说，价值为1的这条边对其它路程的贡献减少了

我们来举一个例子

在左边这幅图中，我们没有把价值为1的边放在价值为0的边的旁边，这时(u,B)这条边永远会缺失1，我们从v向下遍历，同时经过0和1的路径的个数会减少，会有很多路径的价值为1，以后也不会再改变

在右边这幅图中，我们有把价值为1的边放在价值为0的边的旁边，这时(u,B)这条边的边权1，它的价值也就为1，我们从v向下遍历，同时经过0和1的路径的个数显然要比上面的多，路径的价值一定会大于1

同样的，我们可以把2 、3、4……n-1（不一定会加到n-1，原因我们后面会说）依次填入，只要按照上面的方法就可以

但是还有一个问题，我们是从左边加还是从右边加呢

这是我们就需要用到动态转移方程取较大值

f[u][v]=max(f[u,pa[u][v]],f[v,pa[v][u]])+g[u][v]*g[v][u]

什么意思呢，我们还是拿图来说

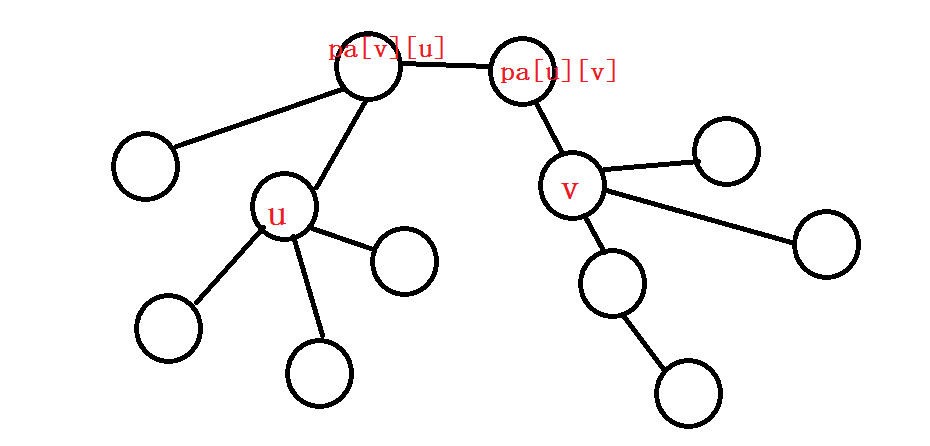
我们假设u和v之间的边权都已经从小到大加完，那么其中最大的一个权值我们不是加在（u,pa[v][u]）上，就是加在（v,pa[u][v]）上

如果加在（u,pa[v][u]）上，那么增大的价值就是g[u][v]*g[v][u]，还要加上原来就有的f[u,pa[u][v]]

如果加在（v,pa[u][v]）上，那么增大的价值就是g[u][v]*g[v][u]，还要加上原来就有的f[v,pa[v][u]]

实际上这两种情况增大的价值都是一样的，我们只需要在f[u,pa[u][v]]和f[v,pa[v][u]]中取最大值就可以了

最后我们再看一下最后的决策是什么情况

根据我们一开始的推论，边权从小到大一定会加在同一条链上，但是这一条链不一定会包含n-1条边，就像下面这样

标红色的是我们已经选好边权的边

这时我们会发现（2，3）（4，7）这两条边并没有被赋上相应的价值，这时该怎么办呢，最后的价值还是f[8][9]吗？

答案是肯定的，此时边权只剩下了最大的两个，无论加到那一条边上都不会对结果产生影响

那么3、7节点贡献的价值呢，实际上，在我们决策2、1、4这三个点时，3、7作为子树价值已经被确定了，无论你加多大的边权也不会改变路程没有经过的最小非负整数

代码的话，g、pa数组我们可以预处理得到，f数组我们枚举取最大值就可以了

这道题也要开long long否则会爆掉

代码

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<iostream>

 #include<cmath>

 using namespace std;

 const int maxd=;

 typedef long long ll;

 struct asd{

     ll from,to,next;

 }b[maxd*];

 ll head[maxd],tot=;

 void ad(ll aa,ll bb){

     b[tot].from=aa;

     b[tot].to=bb;

     b[tot].next=head[aa];

     head[aa]=tot++;

 }

 ll pa[maxd][maxd],f[maxd][maxd],g[maxd][maxd];

 ll rt=;

 void dfs(ll now,ll fa){

     g[rt][now]=;

     for(ll i=head[now];i!=-;i=b[i].next){

         ll u=b[i].to;

         if(u==fa) continue;

         pa[rt][u]=now;

         dfs(u,now);

         g[rt][now]+=g[rt][u];

     }

 }

 ll solve(ll u,ll v){

     if(u==v) return ;

     if(f[u][v]) return f[u][v];

     return f[u][v]=max(solve(u,pa[u][v]),solve(v,pa[v][u]))+g[u][v]*g[v][u];

 }

 int main(){

     memset(head,-,sizeof(head));

     ll n;

     scanf("%lld",&n);

     for(ll i=;i<n;i++){

         ll aa,bb;

         scanf("%lld%lld",&aa,&bb);

         ad(aa,bb);

         ad(bb,aa);

     }

     for(ll i=;i<=n;i++){

         rt=i;

         dfs(i,-);//递归，预处理s数组和pa数组

     }

     ll ans=-;

     for(ll i=;i<=n;i++){

         for(ll j=;j<=n;j++){

             ans=max(solve(i,j),ans);//取最大值

         }

     }

     printf("%lld\n",ans);

     return ;

 }