Relatives POJ - 2407 欧拉函数

题意：

给你一个正整数n，问你在区间[1,n）中有多少数与n互质

题解：

1既不是合数也不是质数（1不是素数）

互质是公约数只有1的两个整数，叫做互质整数。公约数只有1的两个自然数，叫做互质自然数 所以1与任何整数都互质

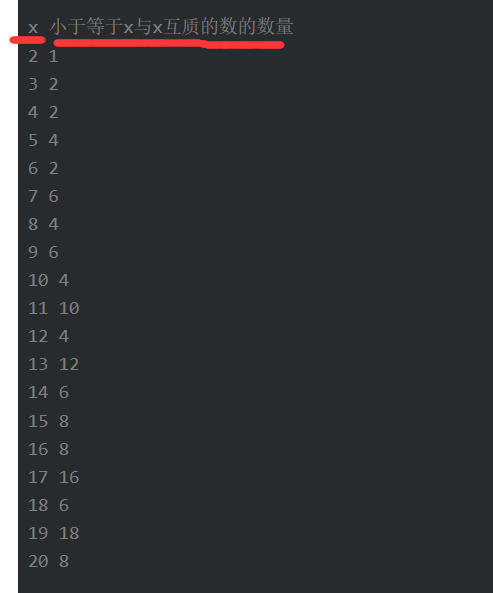
根据欧拉函数求解 欧拉函数是少于或等于n的数中与n互质的数的数目。 欧拉函数的性质：它在整数n上的值等于对n进行素因子分解后，所有的素数幂上的欧拉函数之积。 欧拉函数的值 　通式：φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn),其中p1, p2……pn为x的所有质因数，x是不为0的整数。 φ(1)=1（唯一和1互质的数(小于等 于1)就是1本身）。 (注意：每种质因数只一个。比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4）

推论：当n为奇数时，有φ(2n)=φ(n)。

若n是质数p的k次幂，φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)，因为除了p的倍数外，其他数都跟n互质。 设n为正整数，以 φ(n)表示不超过n且与n互素的正整数的个数，称为n的欧拉函数值，这里函数φ：N→N，n→φ(n)称为欧拉函数。 欧拉函数是积性函数——若m,n互质，φ(mn)=φ(m)φ(n)。

特殊性质：当n为奇数时，φ(2n)=φ(n), 证明与上述类似。

解释：

1、为什么欧拉函数是φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn)

两个数互质是除了1不能有其他公约数 如果一个数和n互质，那么他们就没有公因数，那么我们让总数减去所有与n有公因数的数的数量就可以了 比如与n有公因数x的数的数量有多少，那不就有n/x个嘛。

所以就是这样慢慢减

2、当n为奇数时，有φ(2n)=φ(n)。

我们要求2n的互质数量，那么2n与公因数为2的数的数量由n个，所以可以说1——n这一段数都不与2n互质

代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<iostream>
 4 #include<algorithm>
 5 #include<math.h>
 6 using namespace std;
 7 typedef long long ll;
 8 const int maxn=100005;
 9 int oula(int n)
10 {
11     int ans=n;
12     for(int i=2; i<=sqrt(n); ++i)
13     {
14         if(n%i==0)
15         {
16             ans=ans-ans/i;
17             n/=i;
18             while(n%i==0)
19                 n/=i;
20         }
21     }
22     if(n>1)
23         ans=ans-ans/n;
24     return ans;
25 }
26 int main()
27 {
28     int n;
29     while(~scanf("%d",&n) && n)
30     {
31         int result=oula(n);
32         printf("%d\n",result);
33     }
34     return 0;
35 }