使用Sophus练习李群SO3、SE3以及对应的李代数so3、se3
这是高博《视觉SLAM14讲,从理论到实践》第4章的练习。加了一些注释和理解:
#include <iostream>
#include <cmath>
using namespace std;
#include <Eigen/Core>
#include <Eigen/Geometry>
#include "sophus/so3.h"
#include "sophus/se3.h"
int main( int argc, char** argv )
{
// 沿Z轴转90度的“旋转矩阵”
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
Sophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接从“旋转矩阵”构造
Sophus::SO3 SO3_v( 0, 0, M_PI/2 ); // 亦可从“旋转向量”构造
Eigen::Quaterniond q(R); // 或者“四元数”
Sophus::SO3 SO3_q( q );
// 上述表达方式都是等价的
// 输出SO(3)时,以 "旋转向量(角+轴)" 形式输出
cout<<"SO(3) from matrix: "<<SO3_R<<endl;
cout<<"SO(3) from vector: "<<SO3_v<<endl;
cout<<"SO(3) from quaternion :"<<SO3_q<<endl;
Eigen::Vector3d so3 = SO3_R.log(); // 使用 "对数映射" 获得它的李代数
cout<<"so3 = "<<so3.transpose()<<endl;
cout<<"so3 hat=\n"<<Sophus::SO3::hat(so3)<<endl;// hat 为向量-------->矩阵
// 相对的,vee为反对称到向量
cout<<"so3 hat vee= "<<Sophus::SO3::vee( Sophus::SO3::hat(so3) ).transpose()<<endl; // transpose纯粹是为了输出美观一些
// 增量扰动模型的更新
Eigen::Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多
Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3)*SO3_R;
cout<<"SO3 updated = "<<SO3_updated<<endl;
cout<<"*******************萌萌的分割线*****************************"<<endl;;
// 对SE(3)操作大同小异
Eigen::Vector3d t(1,0,0); // 沿X轴平移1-----------平移部分
Sophus::SE3 SE3_Rt(R, t); // 从R,t构造SE(3)-------旋转(旋转矩阵)+平移
Sophus::SE3 SE3_qt(q,t); // 从q,t构造SE(3)--------旋转 (四元数) +平移
cout<<"SE3 from R,t= "<<endl<<SE3_Rt<<endl;
cout<<"SE3 from q,t= "<<endl<<SE3_qt<<endl;
// 李代数se(3) 是一个六维向量,方便起见先typedef一下
typedef Eigen::Matrix<double,6,1> Vector6d; //6*1的double矩阵
Vector6d se3 = SE3_Rt.log(); // 使用 "对数映射" 获得它的李代数se3
cout<<"se3 = "<<se3.transpose()<<endl;
// 观察输出,会发现在Sophus中,se(3)的平移在前,旋转在后.
// 同样的,有hat和vee两个算符
cout<<"se3 hat = "<<endl<<Sophus::SE3::hat(se3)<<endl;
cout<<"se3 hat vee = "<<Sophus::SE3::vee( Sophus::SE3::hat(se3) ).transpose()<<endl;
// 最后,演示一下更新
Vector6d update_se3; //更新量
update_se3.setZero();
update_se3(0,0) = 1e-4d;
Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3)*SE3_Rt;
cout<<"SE3 updated = "<<endl<<SE3_updated.matrix()<<endl;
return 0;
}
结果如下:
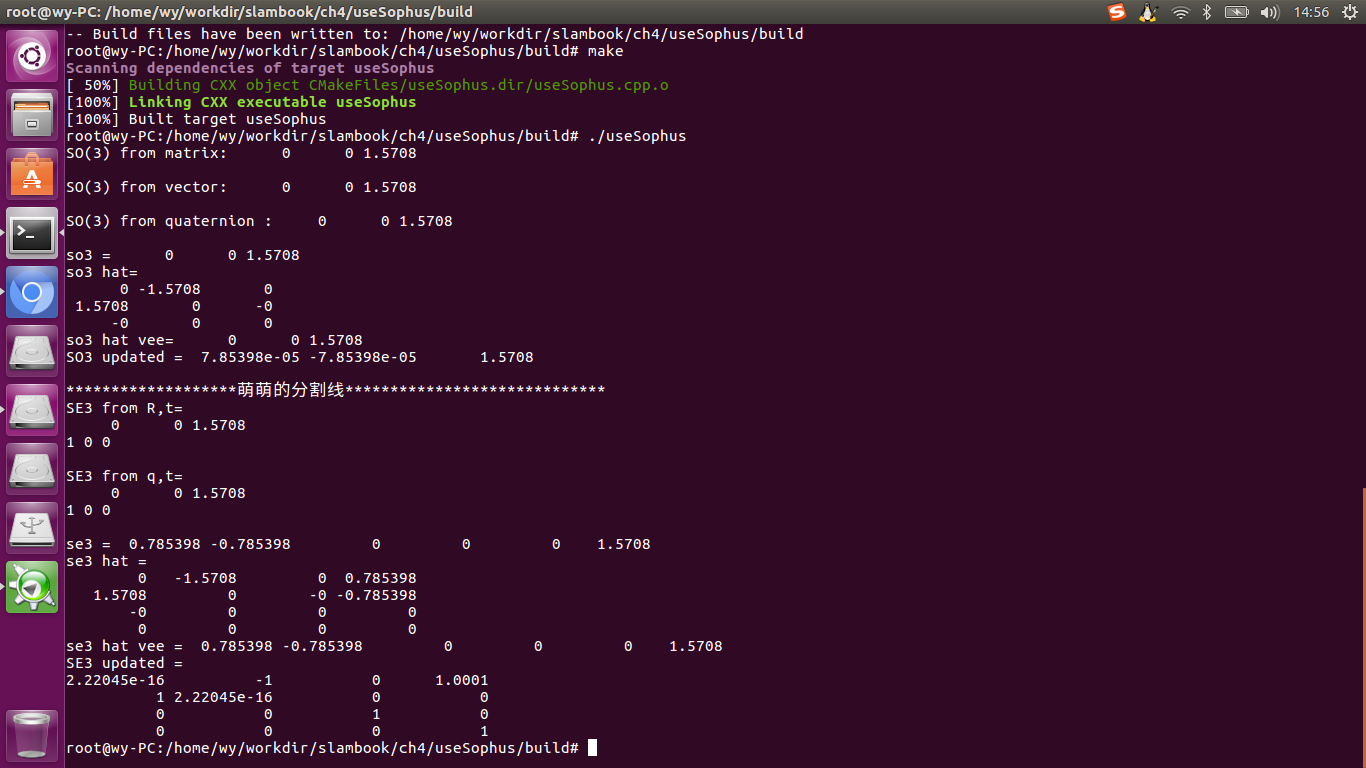
使用Sophus练习李群SO3、SE3以及对应的李代数so3、se3的更多相关文章
- 从零开始一起学习SLAM | 为啥需要李群与李代数?
很多刚刚接触SLAM的小伙伴在看到李群和李代数这部分的时候,都有点蒙蒙哒,感觉突然到了另外一个世界,很多都不自觉的跳过了,但是这里必须强调一点,这部分在后续SLAM的学习中其实是非常重要的基础,不信你 ...
- lsdslam代码笔记
0.1. question 0.2. 算法框架 0.3. 代码解析 0.3.1. 数据结构 0.3.1.1. Frame 0.3.1.2. FrameMemory 0.3.1.3. FramePose ...
- 【python之路11】集合数据类型(set)
集合数据类型(set):集合是不重复的无需序列 1.集合数据类型的创建 a = {11,22,33} #或 a = set() #创建空集合,不能用a={},这样创建的是字典类型 2.集合转换(将可迭 ...
- 音乐代码 (DNF天空之城、欢乐颂)。
太感人了 DNF天空之城 #include <cstdio> #include <windows.h> #define qdo 262 #define qre 294 #def ...
- python基础(一)—— 核心数据类型
Hello World程序 [root@mysql ~]# python3 Python 3.6.5 (default, Jul 8 2018, 11:41:23) [GCC 4.4.7 20120 ...
- Google Cardboard的九轴融合算法——基于李群的扩展卡尔曼滤波
Google Cardboard的九轴融合算法 --基于李群的扩展卡尔曼滤波 极品巧克力 前言 九轴融合算法是指通过融合IMU中的加速度计(三轴).陀螺仪(三轴).磁场计(三轴),来获取物体姿态的方法 ...
- Sophus链接错误
错误指示如下: CMakeFiles/run_vo.dir/run_vo.cpp.o: In function `main': run_vo.cpp:(.text.startup+0x1086): u ...
- Sophus libSophus.so
在编译包含Sophus的源文件的时候,出现如下错误 ../lib/libmyslam.so: undefined reference to `Sophus::SO3::SO3(double, doub ...
- Sophus库CMakeLists.txt内容详解笔记
CMakeLists.txt: SET(PROJECT_NAME Sophus) PROJECT(${PROJECT_NAME}) CMAKE_MINIMUM_REQUIRED(VERSION 2.6 ...
随机推荐
- CF:Problem 427C - Checkposts强连通 Tarjan算法
tarjan算法第一题 喷我一脸. ...把手写栈的类型开成了BOOL.一直在找错.. . #include<cstdio> #include<cstring> #includ ...
- 【bzoj3208】花神的秒题计划Ⅰ
记忆化搜索 #include<algorithm> #include<iostream> #include<cstring> #include<cstdlib ...
- web前端和后端的区别
一句话,展示ui相关的就是前端,否则就是后端. 前端语言:javascript.css和html. 后端就是一些服务.
- GeHost powershell
PS C:\Users\clu\Desktop> [System.Net.Dns] | Get-Member -Static | Format-Table -AutoSize TypeName: ...
- iOS如何查看静态库.a文件支持的cpu类型
打开终端: 输入 lipo -info 然后将你要查看的静态库.a 文件找到,拖入 -info 后边.假设路径为A,即为 lipo -info A 回车键,然后就会看到静态库是否支持 armv7,ar ...
- 【CSU 1079】树上的查询
http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1079 现有一棵有N个顶点的树,顶点的标号分别为1, 2, …, N.对于每个形如a b k的询问, ...
- 洛谷 P1314 聪明的质监员 —— 二分
题目:https://www.luogu.org/problemnew/show/P1314 显然就是二分那个标准: 当然不能每个区间从头到尾算答案,所以要先算出每个位置被算了几次: 不知为何自己第一 ...
- Real-Time Compressive Tracking,实时压缩感知跟踪算法解读
这是Kaihua Zhang发表在ECCV2012的paper,文中提出了一种基于压缩感知(compressive sensing)的单目标跟踪算法,该算法利用满足压缩感知(compressive s ...
- Unity ScriptObject
http://godstamps.blogspot.com/2012/02/unity-3d-scriptableobject-assetbundle.html http://ivanozanchet ...
- bzoj1770: [Usaco2009 Nov]lights 燈(折半搜索)
1770: [Usaco2009 Nov]lights 燈 Time Limit: 10 Sec Memory Limit: 64 MBSubmit: 1153 Solved: 564[Submi ...
