hiho一下 第四十九周 题目1 : 欧拉路·一【无向图 欧拉路问题】

题目1 : 欧拉路·一

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi和小Ho最近在玩一个解密类的游戏，他们需要控制角色在一片原始丛林里面探险，收集道具，并找到最后的宝藏。现在他们控制的角色来到了一个很大的湖边。湖上有N个小岛(编号1..N)，以及连接小岛的M座木桥。每座木桥上各有一个宝箱，里面似乎装着什么道具。

湖边还有一个船夫，船夫告诉主角。他可以载着主角到任意一个岛上，并且可以从任意一个岛上再载着主角回到湖边，但是主角只有一次来回的机会。同时船夫告诉主角，连接岛屿之间的木桥很脆弱，走过一次之后就会断掉。

因为不知道宝箱内有什么道具，小Hi和小Ho觉得如果能把所有的道具收集齐肯定是最好的，那么对于当前岛屿和木桥的情况，能否将所有道具收集齐呢？

举个例子，比如一个由6个小岛和8座桥组成的地图：

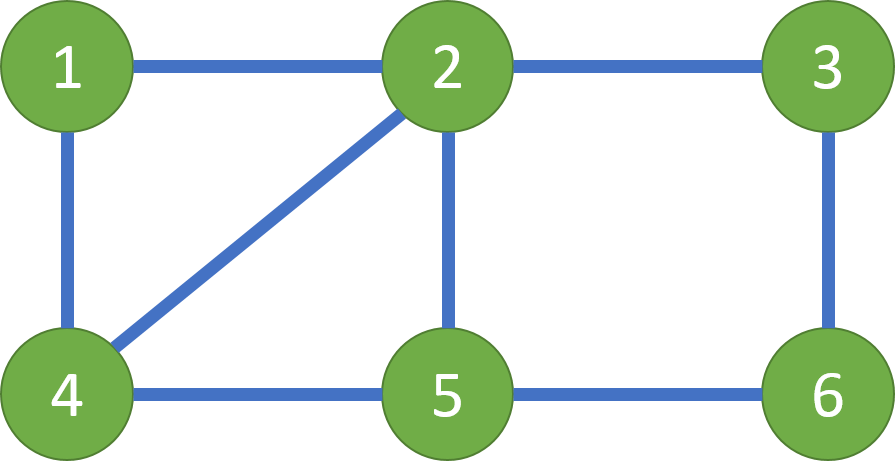
主角可以先到达4号小岛，然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛，然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。

提示：欧拉路的判定

输入

第1行：2个正整数，N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000，1≤M≤50,000

第2..M+1行：每行2个整数，u,v。表示有一座木桥连接着编号为u和编号为v的岛屿，两个岛之间可能有多座桥。1≤u,v≤N

输出

第1行：1个字符串，如果能收集齐所有的道具输出“Full”，否则输出”Part”。

样例输入

6 8
1 2
1 4
2 4
2 5
2 3
3 6
4 5
5 6

样例输出

Full
算法分析：这道题目就是让你画一个一笔画，刚好经过所有的边一次即可，是关于欧拉路的问题。简单的把欧拉路径分一下类（基于无向
图）：
1). 欧拉回路：图G的一个回路，若它恰通过图G中每条边仅一次，则称该回路为欧拉回路。（起点、终点相同）
解法：图G连通+度数为奇数的点的个数为0.
2). 具有欧拉回路的图成为欧拉图。
3). 欧拉图的变形：就是可以不会到原来的起点，但是仍要经历所有的边各一次，也就是所谓的一笔画问题。
解法：图G连通+度数为奇数的点的个数为2.一个是起点，一个是终点。
本题目中有提到说：两个点之间可能存在多条边，注意即使是存在多条变，每条边也都要遍历到才能满足要求。也就是，只要有边，该边
两个端点对应的节点的度数就要累加。
代码：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#include <math.h>
#include <iostream>
#include <string>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#include <algorithm>
#define LL long long int
#define N 10000+10

using namespace std;
int n, m;
//1≤N≤10000  1≤M≤50000
//欧拉路的判定(不是欧拉回路)
//因为可以不必回到起点， 所以是欧拉路的变形
//1)必须是连通图 2)奇数度的点的个数必须为2

unsigned int in[N];
vector<int>qm[N];
bool vis[N];

bool dfs(int u)
{
    vis[u]=true;
    for(int i=0; i<qm[u].size(); i++)
    {
        if(vis[qm[u][i]]==false )
        {
            vis[qm[u][i]]=true;
            dfs(qm[u][i]);
        }
    }
}

int main()
{
    scanf("%d %d", &n, &m);
    int i, j;
    memset(in, 0, sizeof(in));
    for(i=0; i<=n; i++)
        qm[i].clear();

    int u, v;
    for(i=0; i<m; i++){
        scanf("%d %d", &u, &v );
        qm[u].push_back(v);
        qm[v].push_back(u);
        in[u]++;
        in[v]++;
    }
    memset(vis, false, sizeof(vis));
    dfs(1);
    bool flag=true;
    for(i=1; i<=n; i++){
        if(vis[i]==false){
            flag=false; break;
        }
    }
    int cnt=0;
    for(i=1; i<=n; i++)
    {
        if(in[i]%2==1 )
            cnt++;
    }
    if(flag==true && (cnt==2 || cnt==0))
        printf("Full\n");
    else
        printf("Part\n");

    return 0;
}

静态数组模拟：

注意：存储边的数组要开大一些，并不是开m条边的大小，会RE的，需要开更大，因为是双向边。

代码：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#include <math.h>
#include <iostream>
#include <string>
#include <algorithm>
#define LL long long int
#define N 10000+100
#define M 60000+100

using namespace std;
int n, m;
//1≤N≤10000  1≤M≤50000
//欧拉路的判定(不是欧拉回路)
//因为可以不必回到起点， 所以是欧拉路的变形
//1)必须是连通图 2)奇数度的点的个数必须为2

unsigned int in[N];
bool vis[N];

int edgecnt;
int head[N]={0};
int p[M];
int Next[M]={0};

void addedge(int u, int v)
{
    ++edgecnt;
    p[edgecnt]=v;
    Next[edgecnt]=head[u];
    head[u]=edgecnt;
}

bool dfs(int u)
{
    int i;
    for(i=head[u]; i; i=Next[i])
    {
        if(vis[p[i]]==false )
        {
            vis[p[i]]=true;
            dfs(p[i]);
        }
    }
}

int main()
{
    scanf("%d %d", &n, &m);
    int i, j;
    memset(in, 0, sizeof(in));

    int u, v;
    edgecnt=0;
    for(i=0; i<m; i++){
        scanf("%d %d", &u, &v );
        addedge(u, v);
        addedge(v, u);
        in[u]++;
        in[v]++;
    }
    memset(vis, false, sizeof(vis));
    vis[1]=true;
    dfs(1);
    bool flag=true;
    for(i=1; i<=n; i++){
        if(vis[i]==false){
            flag=false; break;
        }
    }

    int cnt=0;
    for(i=1; i<=n; i++)
    {
        if(in[i]%2==1 )
            cnt++;
    }
    if(flag==true && (cnt==2 || cnt==0))
        printf("Full\n");
    else
        printf("Part\n");

    return 0;
}

这是是十佳代码里的最短的代码，居然和我写的代码一样的算法实现，吓坏我了~~~

#include<cstdio>
int d[10001],N,M,v;
main()
{
    for(scanf("%d%d",&N,&M); M--; d[*d]++,d[v]++)
        scanf("%d%d",d,&v);
    for(; N;)M+=d[N--]&1;
    puts(M>2?"Part":"Full");
}