SVM – 核函数

　　核函数的起源是对于线性不可分的分类情况，其实可以通过p次方多项式，及非线性模型进行分类；然后对于这类非线性多次方的，其实可以按照广义线性模型来进行升维变形，使之成为线性模型，这样就可以放到SVM中来进行处理了（svm只能处理非线性模型）。

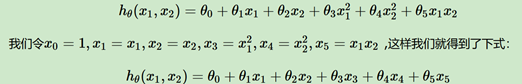
　　但是升维之后是有维度爆炸现象的（二次方对应6维度，三次方对应19维度），为了解决这个问题，核函数出场了，简单讲核函数就是计算计算是在低维进行，但是形式却是映射到高维。

　　SVM的优化目标：

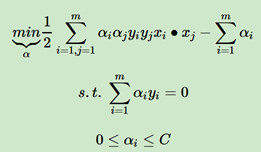
　　假设xi和xj都是低维非线性的函数，我们定义映射到高维的函数为φ(x)，那么上面的式子可以写成：

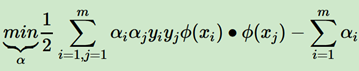
　　核函数，就是实现了计算在低维计算，返回形式是高维：

K(x, z) = φ(x) * φ(z)

　　但是这种映射并不是容易获取的，需要满足Gram矩阵K = [K(x,z)]是半正定型，也就是说，一个函数想要成为核函数，必须要满足里面任何点的集合形成的Gram矩阵是半正定矩阵。

　　这里解释一下，gram矩阵是指n维欧式空间中任意k个向量内积组成的矩阵：

　　关于正定矩阵：M是n阶方阵，对于非0向量，z.T *M*z > 0，矩阵的乘法还是矩阵，这里> 0，我理解是因为乘法形式的行列式的值是大于0的。

　　半正定矩阵和正定矩阵就是一字之差：z.T * M * z >= 0，半正定允许等于0，所以范围更加宽广，所以血统不那么纯正，所以称之为半正定（越纯正要求越严格）。

　　话题再扯回来，如果想要满足核函数，那么函数K的矩阵要满足Gram矩阵是半正定的；这个门槛其实很高的，好在我们数学大佬们已经带我们走出探索的沼泽，并且亲自指出了常用的核函数与：

　　线性核函数(Linear Kernel)：

　　K(x, z) = x·z，线性svm就是使用这个核函数；

　　多项式核函数(Polynomial Kernel)：

　　k(x, z) = (γx·z + r)^d，其中gamma，r以及d需要自己调参；

　　高斯核函数（Gaussian Kernel)，也称之为径向基和函数（Radial Basis Function,RBF）：

　　K(x, z）=xp(−γ||x−z||²)

　　Sigmoid核函数：

　　K(x,z)=tanh（γx∙z+r)，其中γ和r需要自己调参；

参考：

https://www.cnblogs.com/pinard/p/6103615.html