C#基于ScottPlot进行可视化
C#基于ScottPlot进行可视化
前言
上一篇文章跟大家分享了用NumSharp实现简单的线性回归，但是没有进行可视化，可能对拟合的过程没有直观的感受，因此今天跟大家介绍一下使用C#基于Scottplot进行可视化，当然Python的代码，我也会同步进行可视化。
Python代码进行可视化
Python代码用matplotlib做了可视化，我就不具体介绍了。
修改之后的python代码如下：
#The optimal values of m and b can be actually calculated with way less effort than doing a linear regression.
#this is just to demonstrate gradient descent
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (m * x + b)) ** 2
return totalError / float(len(points))
def step_gradient(b_current, m_current, points, learningRate):
b_gradient = 0
m_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
b_gradient += -(2/N) * (y - ((m_current * x) + b_current))
m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))
new_b = b_current - (learningRate * b_gradient)
new_m = m_current - (learningRate * m_gradient)
return [new_b, new_m]
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
b = starting_b
m = starting_m
args_data = []
for i in range(num_iterations):
b, m = step_gradient(b, m, np.array(points), learning_rate)
args_data.append((b,m))
return args_data
if __name__ == '__main__':
points = np.genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_m = 0 # initial slope guess
num_iterations = 10
print ("Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points)))
print ("Running...")
args_data = gradient_descent_runner(points, initial_b, initial_m, learning_rate, num_iterations)
b = args_data[-1][0]
m = args_data[-1][1]
print ("After {0} iterations b = {1}, m = {2}, error = {3}".format(num_iterations, b, m, compute_error_for_line_given_points(b, m, points)))
data = np.array(points).reshape(100,2)
x1 = data[:,0]
y1 = data[:,1]
x2 = np.linspace(20, 80, 100)
y2 = initial_m * x2 + initial_b
data2 = np.array(args_data)
b_every = data2[:,0]
m_every = data2[:,1]
# 创建图形和轴
fig, ax = plt.subplots()
line1, = ax.plot(x1, y1, 'ro')
line2, = ax.plot(x2,y2)
# 添加标签和标题
plt.xlabel('x')
plt.ylabel('y')
plt.title('Graph of y = mx + b')
# 添加网格
plt.grid(True)
# 定义更新函数
def update(frame):
line2.set_ydata(m_every[frame] * x2 + b_every[frame])
ax.set_title(f'{frame} Graph of y = {m_every[frame]:.2f}x + {b_every[frame]:.2f}')
# 创建动画
animation = FuncAnimation(fig, update, frames=len(data2), interval=500)
# 显示动画
plt.show()
实现的效果如下所示：
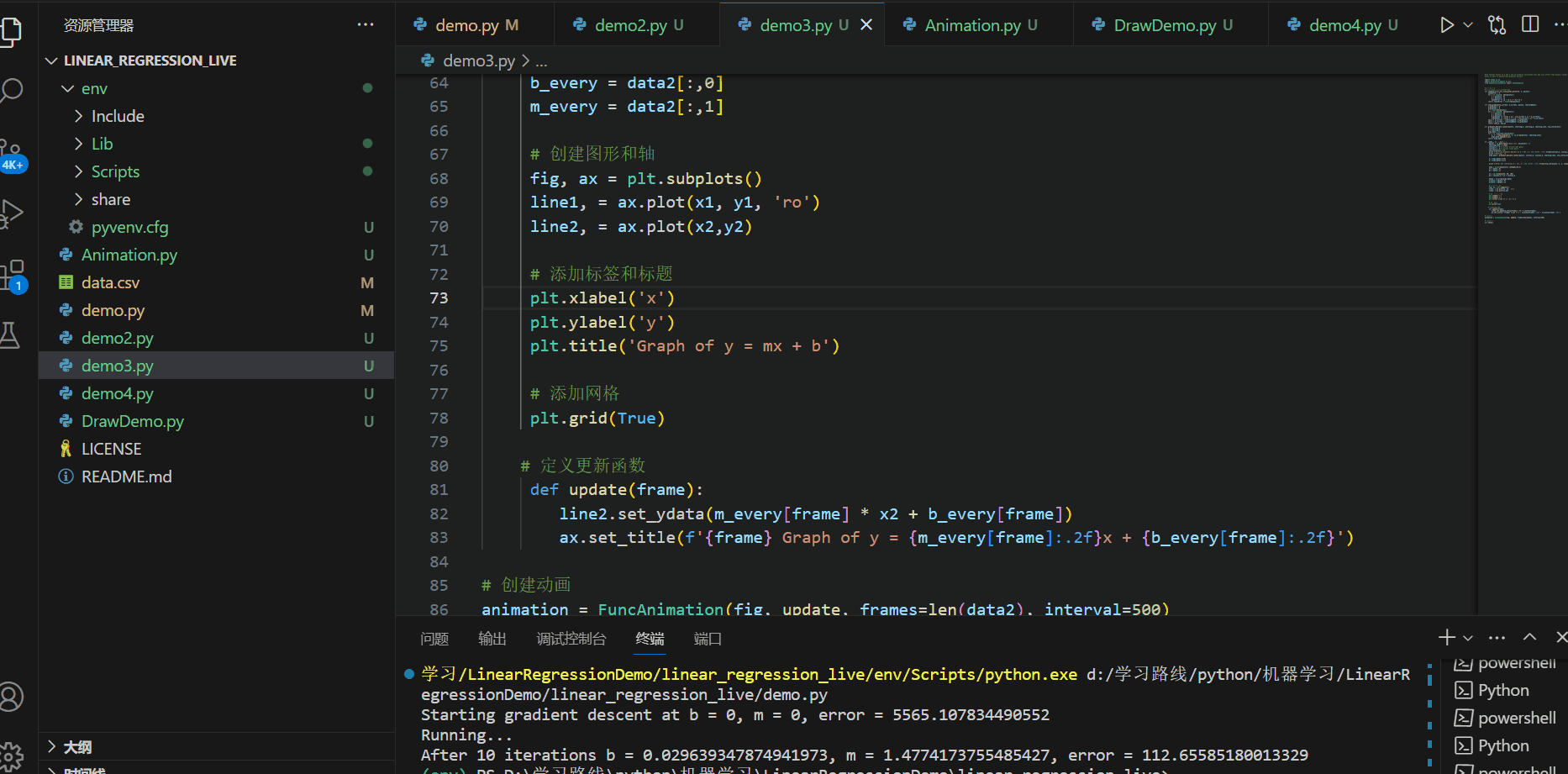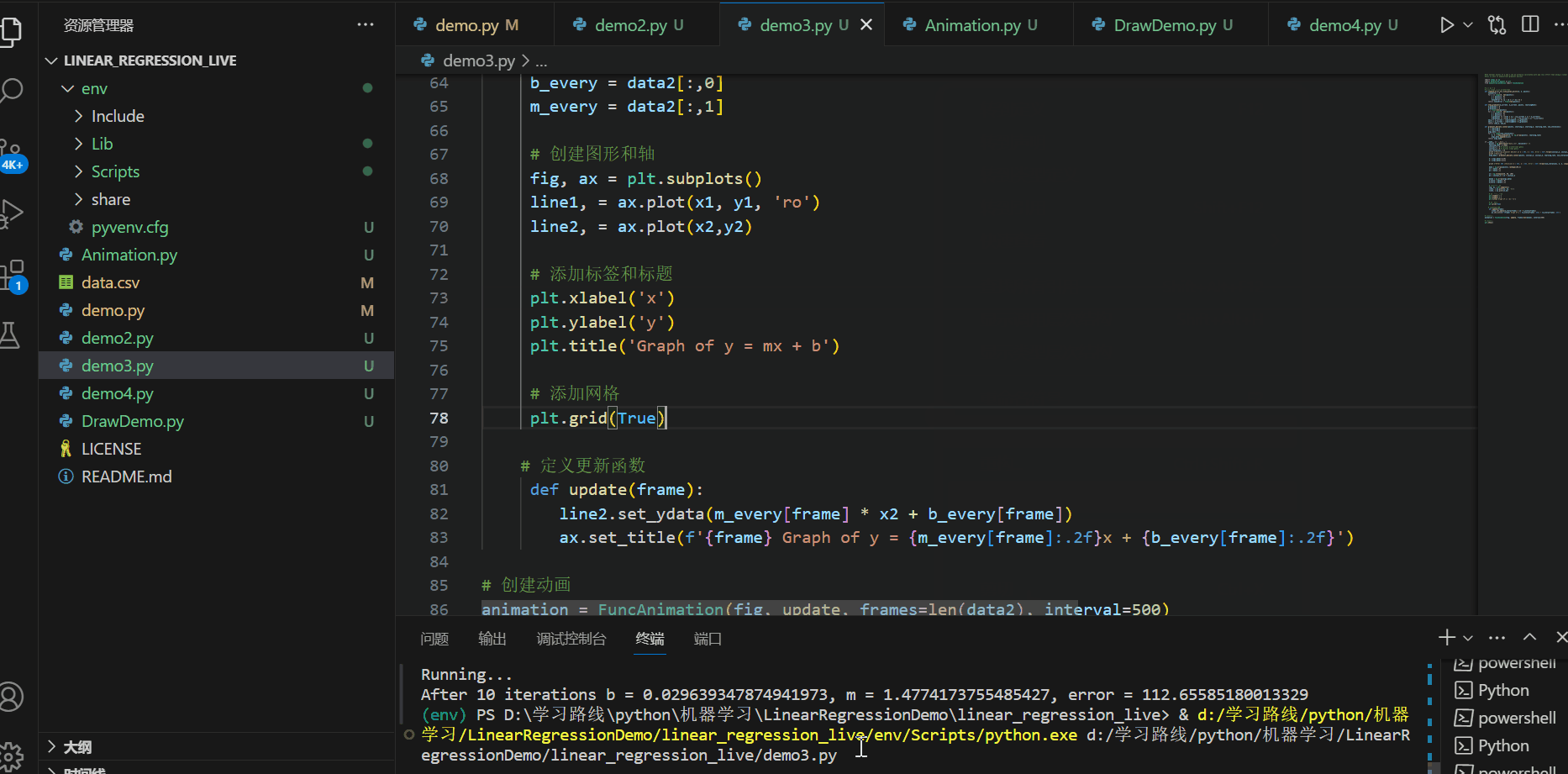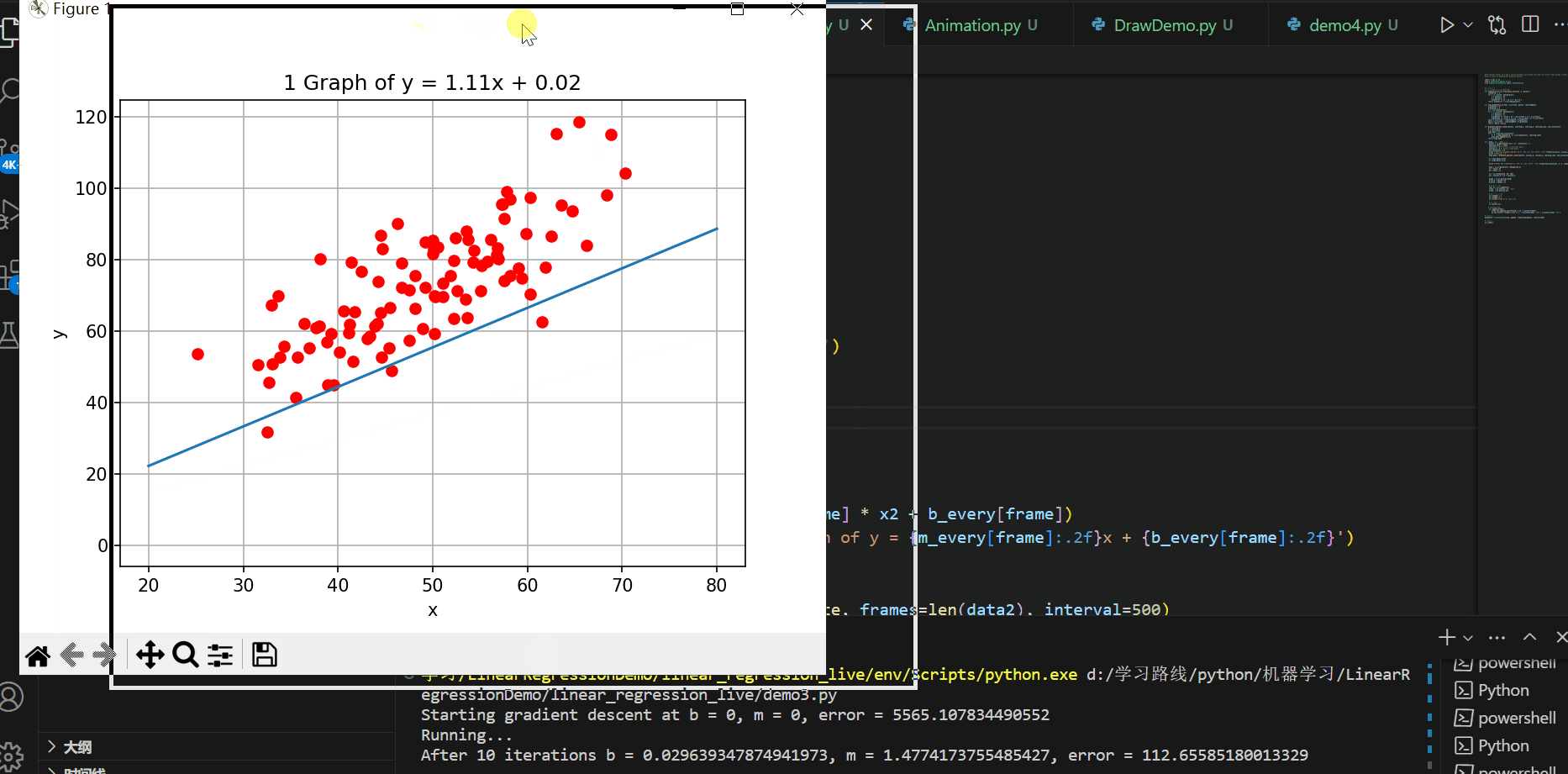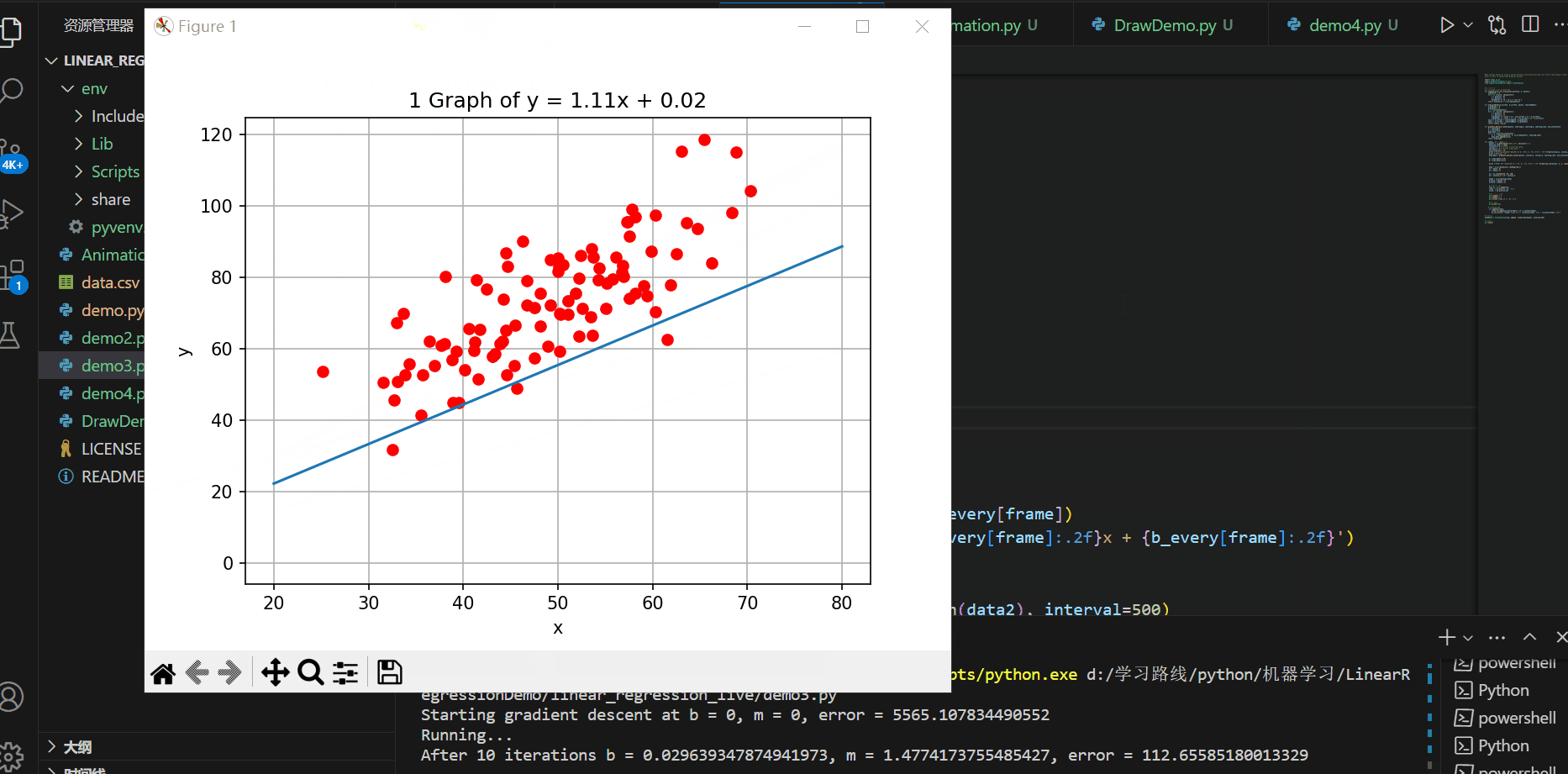
C#代码进行可视化
这是本文重点介绍的内容，本文的C#代码通过Scottplot进行可视化。
Scottplot简介
ScottPlot 是一个免费的开源绘图库，用于 .NET，可以轻松以交互方式显示大型数据集。
控制台程序可视化
首先我先介绍一下在控制台程序中进行可视化。
首先添加Scottplot包：
将上篇文章中的C#代码修改如下：
using NumSharp;
namespace LinearRegressionDemo
{
internal class Program
{
static void Main(string[] args)
{
//创建double类型的列表
List<double> Array = new List<double>();
List<double> ArgsList = new List<double>();
// 指定CSV文件的路径
string filePath = "你的data.csv路径";
// 调用ReadCsv方法读取CSV文件数据
Array = ReadCsv(filePath);
var array = np.array(Array).reshape(100,2);
double learning_rate = 0.0001;
double initial_b = 0;
double initial_m = 0;
double num_iterations = 10;
Console.WriteLine($"Starting gradient descent at b = {initial_b}, m = {initial_m}, error = {compute_error_for_line_given_points(initial_b, initial_m, array)}");
Console.WriteLine("Running...");
ArgsList = gradient_descent_runner(array, initial_b, initial_m, learning_rate, num_iterations);
double b = ArgsList[ArgsList.Count - 2];
double m = ArgsList[ArgsList.Count - 1];
Console.WriteLine($"After {num_iterations} iterations b = {b}, m = {m}, error = {compute_error_for_line_given_points(b, m, array)}");
Console.ReadLine();
var x1 = array[$":", 0];
var y1 = array[$":", 1];
var y2 = m * x1 + b;
ScottPlot.Plot myPlot = new(400, 300);
myPlot.AddScatterPoints(x1.ToArray<double>(), y1.ToArray<double>(), markerSize: 5);
myPlot.AddScatter(x1.ToArray<double>(), y2.ToArray<double>(), markerSize: 0);
myPlot.Title($"y = {m:0.00}x + {b:0.00}");
myPlot.SaveFig("图片.png");
}
static List<double> ReadCsv(string filePath)
{
List<double> array = new List<double>();
try
{
// 使用File.ReadAllLines读取CSV文件的所有行
string[] lines = File.ReadAllLines(filePath);
// 遍历每一行数据
foreach (string line in lines)
{
// 使用逗号分隔符拆分每一行的数据
string[] values = line.Split(',');
// 打印每一行的数据
foreach (string value in values)
{
array.Add(Convert.ToDouble(value));
}
}
}
catch (Exception ex)
{
Console.WriteLine("发生错误: " + ex.Message);
}
return array;
}
public static double compute_error_for_line_given_points(double b,double m,NDArray array)
{
double totalError = 0;
for(int i = 0;i < array.shape[0];i++)
{
double x = array[i, 0];
double y = array[i, 1];
totalError += Math.Pow((y - (m*x+b)),2);
}
return totalError / array.shape[0];
}
public static double[] step_gradient(double b_current,double m_current,NDArray array,double learningRate)
{
double[] args = new double[2];
double b_gradient = 0;
double m_gradient = 0;
double N = array.shape[0];
for (int i = 0; i < array.shape[0]; i++)
{
double x = array[i, 0];
double y = array[i, 1];
b_gradient += -(2 / N) * (y - ((m_current * x) + b_current));
m_gradient += -(2 / N) * x * (y - ((m_current * x) + b_current));
}
double new_b = b_current - (learningRate * b_gradient);
double new_m = m_current - (learningRate * m_gradient);
args[0] = new_b;
args[1] = new_m;
return args;
}
public static List<double> gradient_descent_runner(NDArray array, double starting_b, double starting_m, double learningRate,double num_iterations)
{
double[] args = new double[2];
List<double> argsList = new List<double>();
args[0] = starting_b;
args[1] = starting_m;
for(int i = 0 ; i < num_iterations; i++)
{
args = step_gradient(args[0], args[1], array, learningRate);
argsList.AddRange(args);
}
return argsList;
}
}
}
然后得到的图片如下所示：
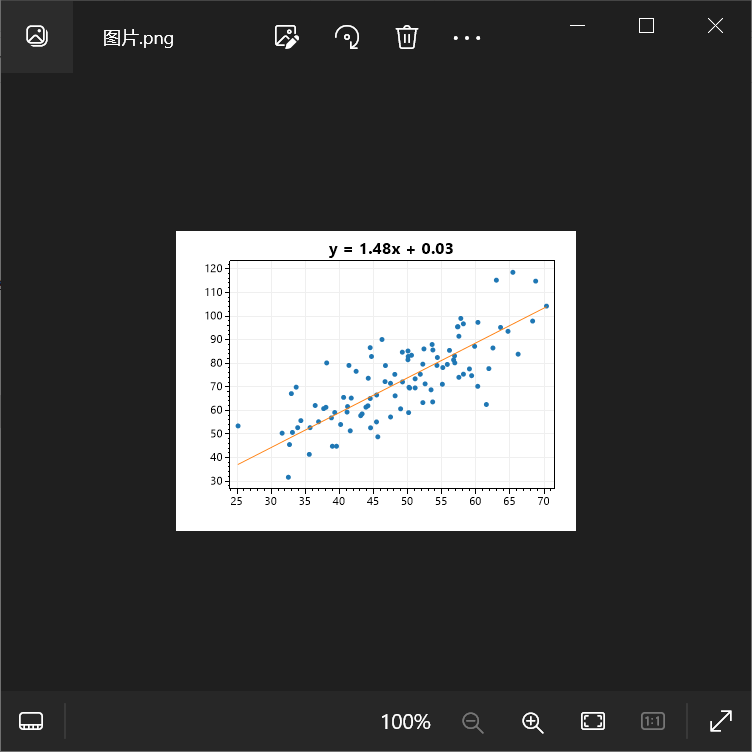
在以上代码中需要注意的地方：
var x1 = array[$":", 0];
var y1 = array[$":", 1];
是在使用NumSharp中的切片，x1表示所有行的第一列，y1表示所有行的第二列。
当然我们不满足于只是保存图片，在控制台应用程序中，再添加一个 ScottPlot.WinForms包：
右键控制台项目选择属性，将目标OS改为Windows：
将上述代码中的
myPlot.SaveFig("图片.png");
修改为：
var viewer = new ScottPlot.FormsPlotViewer(myPlot);
viewer.ShowDialog();
再次运行结果如下：
winform进行可视化
我也想像Python代码中那样画动图，因此做了个winform程序进行演示。
首先创建一个winform，添加ScottPlot.WinForms包，然后从工具箱中添加FormsPlot这个控件：
有两种方法实现，第一种方法用了定时器：
using NumSharp;
namespace WinFormDemo
{
public partial class Form1 : Form
{
System.Windows.Forms.Timer updateTimer = new System.Windows.Forms.Timer();
int num_iterations;
int count = 0;
NDArray? x1, y1, b_each, m_each;
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
StartLinearRegression();
}
public void StartLinearRegression()
{
//创建double类型的列表
List<double> Array = new List<double>();
List<double> ArgsList = new List<double>();
// 指定CSV文件的路径
string filePath = "你的data.csv路径";
// 调用ReadCsv方法读取CSV文件数据
Array = ReadCsv(filePath);
var array = np.array(Array).reshape(100, 2);
double learning_rate = 0.0001;
double initial_b = 0;
double initial_m = 0;
num_iterations = 10;
ArgsList = gradient_descent_runner(array, initial_b, initial_m, learning_rate, num_iterations);
x1 = array[$":", 0];
y1 = array[$":", 1];
var argsArr = np.array(ArgsList).reshape(num_iterations, 2);
b_each = argsArr[$":", 0];
m_each = argsArr[$":", 1];
double b = b_each[-1];
double m = m_each[-1];
var y2 = m * x1 + b;
formsPlot1.Plot.AddScatterPoints(x1.ToArray<double>(), y1.ToArray<double>(), markerSize: 5);
//formsPlot1.Plot.AddScatter(x1.ToArray<double>(), y2.ToArray<double>(), markerSize: 0);
formsPlot1.Render();
}
static List<double> ReadCsv(string filePath)
{
List<double> array = new List<double>();
try
{
// 使用File.ReadAllLines读取CSV文件的所有行
string[] lines = File.ReadAllLines(filePath);
// 遍历每一行数据
foreach (string line in lines)
{
// 使用逗号分隔符拆分每一行的数据
string[] values = line.Split(',');
// 打印每一行的数据
foreach (string value in values)
{
array.Add(Convert.ToDouble(value));
}
}
}
catch (Exception ex)
{
Console.WriteLine("发生错误: " + ex.Message);
}
return array;
}
public static double compute_error_for_line_given_points(double b, double m, NDArray array)
{
double totalError = 0;
for (int i = 0; i < array.shape[0]; i++)
{
double x = array[i, 0];
double y = array[i, 1];
totalError += Math.Pow((y - (m * x + b)), 2);
}
return totalError / array.shape[0];
}
public static double[] step_gradient(double b_current, double m_current, NDArray array, double learningRate)
{
double[] args = new double[2];
double b_gradient = 0;
double m_gradient = 0;
double N = array.shape[0];
for (int i = 0; i < array.shape[0]; i++)
{
double x = array[i, 0];
double y = array[i, 1];
b_gradient += -(2 / N) * (y - ((m_current * x) + b_current));
m_gradient += -(2 / N) * x * (y - ((m_current * x) + b_current));
}
double new_b = b_current - (learningRate * b_gradient);
double new_m = m_current - (learningRate * m_gradient);
args[0] = new_b;
args[1] = new_m;
return args;
}
public static List<double> gradient_descent_runner(NDArray array, double starting_b, double starting_m, double learningRate, double num_iterations)
{
double[] args = new double[2];
List<double> argsList = new List<double>();
args[0] = starting_b;
args[1] = starting_m;
for (int i = 0; i < num_iterations; i++)
{
args = step_gradient(args[0], args[1], array, learningRate);
argsList.AddRange(args);
}
return argsList;
}
private void button2_Click(object sender, EventArgs e)
{
// 初始化定时器
updateTimer.Interval = 1000; // 设置定时器触发间隔（毫秒）
updateTimer.Tick += UpdateTimer_Tick;
updateTimer.Start();
}
private void UpdateTimer_Tick(object? sender, EventArgs e)
{
if (count >= num_iterations)
{
updateTimer.Stop();
}
else
{
UpdatePlot(count);
}
count++;
}
public void UpdatePlot(int count)
{
double b = b_each?[count];
double m = m_each?[count];
var y2 = m * x1 + b;
formsPlot1.Plot.Clear();
formsPlot1.Plot.AddScatterPoints(x1?.ToArray<double>(), y1?.ToArray<double>(), markerSize: 5);
formsPlot1.Plot.AddScatter(x1?.ToArray<double>(), y2.ToArray<double>(), markerSize: 0);
formsPlot1.Plot.Title($"第{count + 1}次迭代：y = {m:0.00}x + {b:0.00}");
formsPlot1.Render();
}
private void button3_Click(object sender, EventArgs e)
{
updateTimer.Stop();
}
private void Form1_Load(object sender, EventArgs e)
{
}
}
}
简单介绍一下思路，首先创建List<double> argsList用来保存每次迭代生成的参数b、m，然后用
var argsArr = np.array(ArgsList).reshape(num_iterations, 2);
将argsList通过np.array()方法转化为NDArray，然后再调用reshape方法，转化成行数等于迭代次数，列数为2，即每一行对应一组参数值b、m。
b_each = argsArr[$":", 0];
m_each = argsArr[$":", 1];
argsArr[$":", 0]表示每一行中第一列的值，也就是每一个b，argsArr[$":", 1]表示每一行中第二列的值。
double b = b_each[-1];
double m = m_each[-1];
b_each[-1]用了NumSharp的功能表示b_each最后一个元素。
实现效果如下所示：
另一种方法可以通过异步实现：
using NumSharp;
namespace WinFormDemo
{
public partial class Form2 : Form
{
int num_iterations;
NDArray? x1, y1, b_each, m_each;
public Form2()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
StartLinearRegression();
}
public void StartLinearRegression()
{
//创建double类型的列表
List<double> Array = new List<double>();
List<double> ArgsList = new List<double>();
// 指定CSV文件的路径
string filePath = "你的data.csv路径";
// 调用ReadCsv方法读取CSV文件数据
Array = ReadCsv(filePath);
var array = np.array(Array).reshape(100, 2);
double learning_rate = 0.0001;
double initial_b = 0;
double initial_m = 0;
num_iterations = 10;
ArgsList = gradient_descent_runner(array, initial_b, initial_m, learning_rate, num_iterations);
x1 = array[$":", 0];
y1 = array[$":", 1];
var argsArr = np.array(ArgsList).reshape(num_iterations, 2);
b_each = argsArr[$":", 0];
m_each = argsArr[$":", 1];
double b = b_each[-1];
double m = m_each[-1];
var y2 = m * x1 + b;
formsPlot1.Plot.AddScatterPoints(x1.ToArray<double>(), y1.ToArray<double>(), markerSize: 5);
formsPlot1.Render();
}
static List<double> ReadCsv(string filePath)
{
List<double> array = new List<double>();
try
{
// 使用File.ReadAllLines读取CSV文件的所有行
string[] lines = File.ReadAllLines(filePath);
// 遍历每一行数据
foreach (string line in lines)
{
// 使用逗号分隔符拆分每一行的数据
string[] values = line.Split(',');
// 打印每一行的数据
foreach (string value in values)
{
array.Add(Convert.ToDouble(value));
}
}
}
catch (Exception ex)
{
Console.WriteLine("发生错误: " + ex.Message);
}
return array;
}
public static double compute_error_for_line_given_points(double b, double m, NDArray array)
{
double totalError = 0;
for (int i = 0; i < array.shape[0]; i++)
{
double x = array[i, 0];
double y = array[i, 1];
totalError += Math.Pow((y - (m * x + b)), 2);
}
return totalError / array.shape[0];
}
public static double[] step_gradient(double b_current, double m_current, NDArray array, double learningRate)
{
double[] args = new double[2];
double b_gradient = 0;
double m_gradient = 0;
double N = array.shape[0];
for (int i = 0; i < array.shape[0]; i++)
{
double x = array[i, 0];
double y = array[i, 1];
b_gradient += -(2 / N) * (y - ((m_current * x) + b_current));
m_gradient += -(2 / N) * x * (y - ((m_current * x) + b_current));
}
double new_b = b_current - (learningRate * b_gradient);
double new_m = m_current - (learningRate * m_gradient);
args[0] = new_b;
args[1] = new_m;
return args;
}
public static List<double> gradient_descent_runner(NDArray array, double starting_b, double starting_m, double learningRate, double num_iterations)
{
double[] args = new double[2];
List<double> argsList = new List<double>();
args[0] = starting_b;
args[1] = starting_m;
for (int i = 0; i < num_iterations; i++)
{
args = step_gradient(args[0], args[1], array, learningRate);
argsList.AddRange(args);
}
return argsList;
}
private void Form2_Load(object sender, EventArgs e)
{
}
public async Task UpdateGraph()
{
for (int i = 0; i < num_iterations; i++)
{
double b = b_each?[i];
double m = m_each?[i];
var y2 = m * x1 + b;
formsPlot1.Plot.Clear();
formsPlot1.Plot.AddScatterPoints(x1?.ToArray<double>(), y1?.ToArray<double>(), markerSize: 5);
formsPlot1.Plot.AddScatter(x1?.ToArray<double>(), y2.ToArray<double>(), markerSize: 0);
formsPlot1.Plot.Title($"第{i + 1}次迭代：y = {m:0.00}x + {b:0.00}");
formsPlot1.Render();
await Task.Delay(1000);
}
}
private async void button2_Click(object sender, EventArgs e)
{
await UpdateGraph();
}
}
}
点击更新按钮开始执行异步任务：
private async void button2_Click(object sender, EventArgs e)
{
await UpdateGraph();
}
public async Task UpdateGraph()
{
for (int i = 0; i < num_iterations; i++)
{
double b = b_each?[i];
double m = m_each?[i];
var y2 = m * x1 + b;
formsPlot1.Plot.Clear();
formsPlot1.Plot.AddScatterPoints(x1?.ToArray<double>(), y1?.ToArray<double>(), markerSize: 5);
formsPlot1.Plot.AddScatter(x1?.ToArray<double>(), y2.ToArray<double>(), markerSize: 0);
formsPlot1.Plot.Title($"第{i + 1}次迭代：y = {m:0.00}x + {b:0.00}");
formsPlot1.Render();
await Task.Delay(1000);
}
实现效果如下：
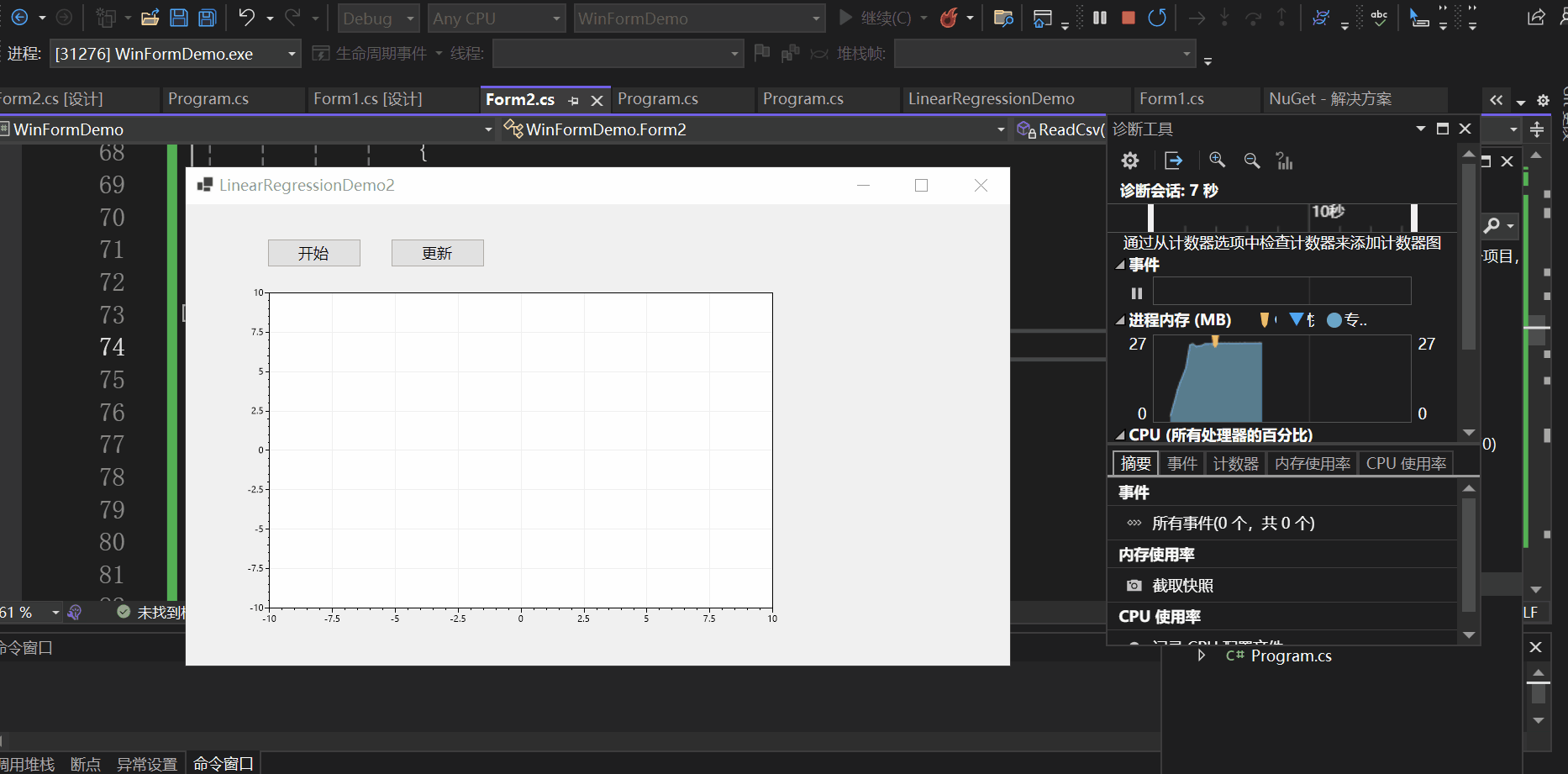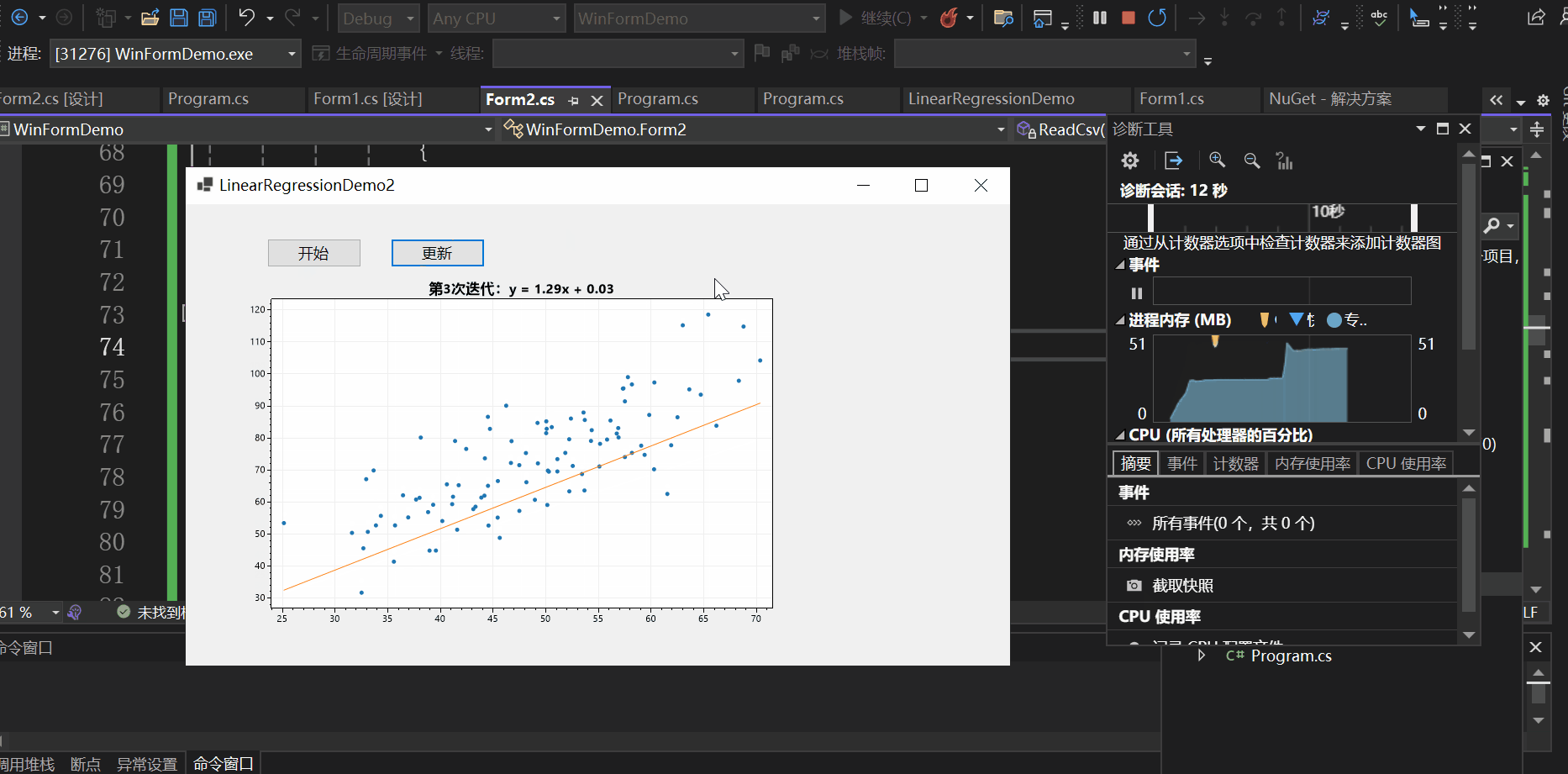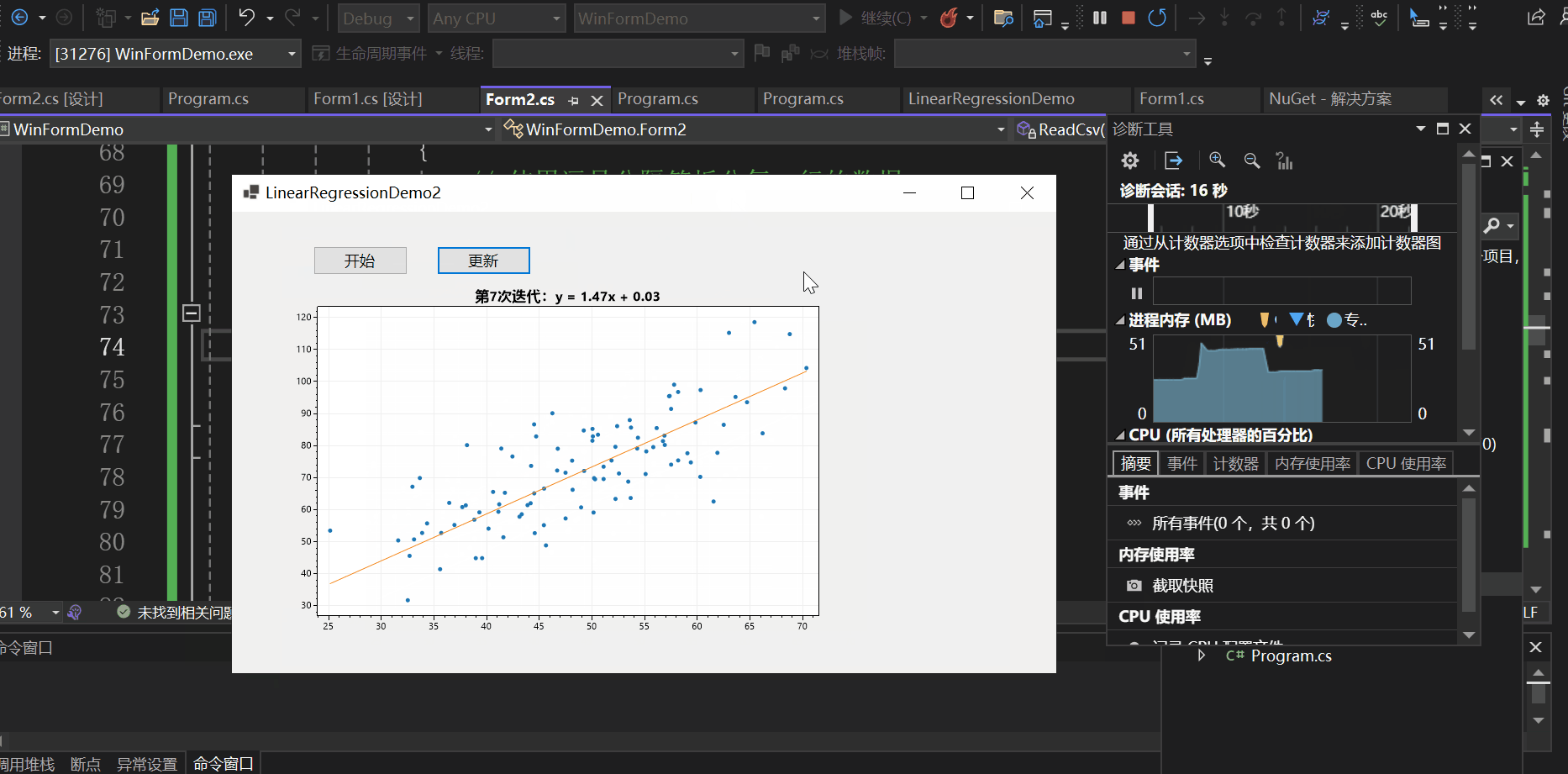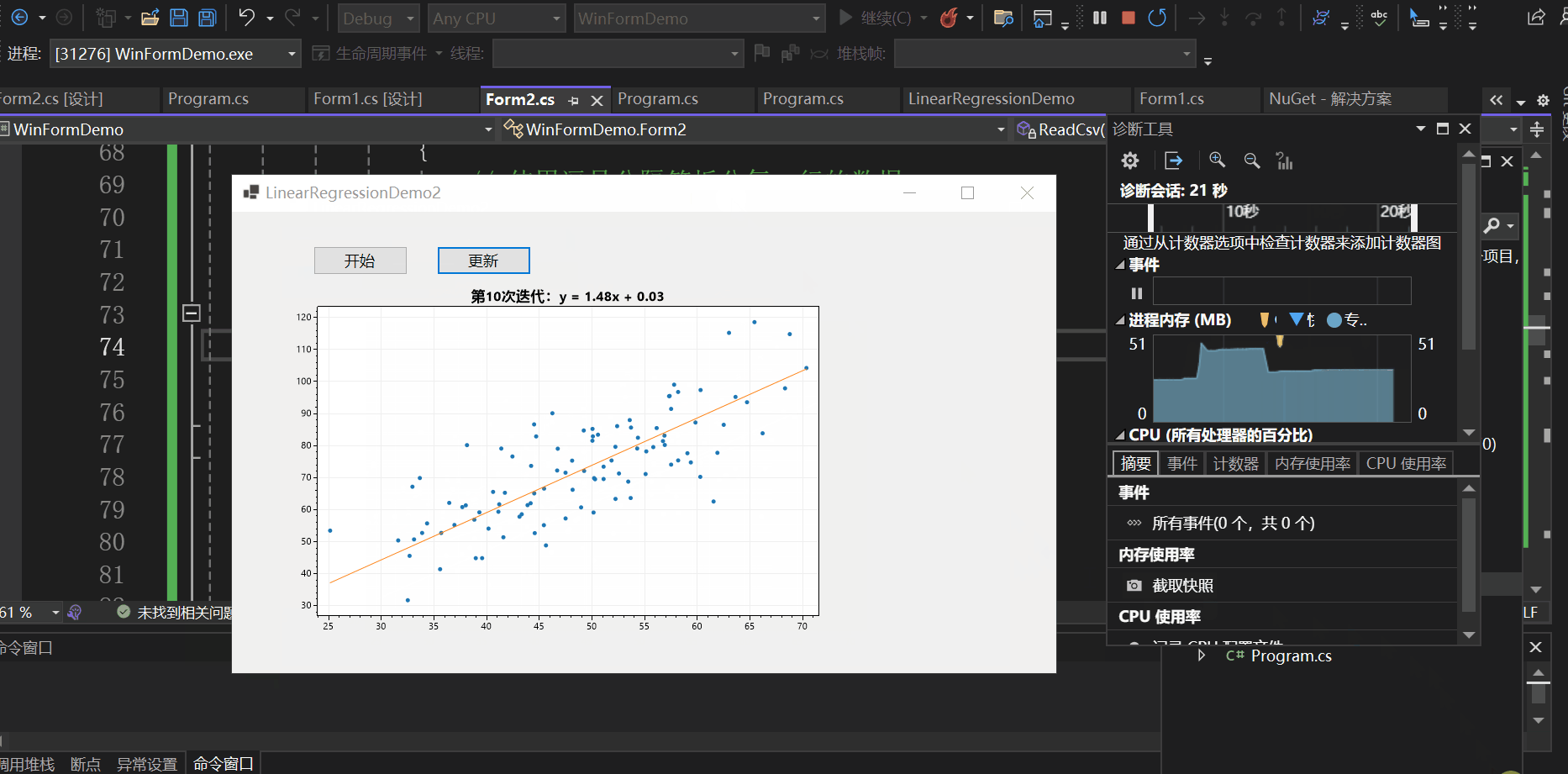
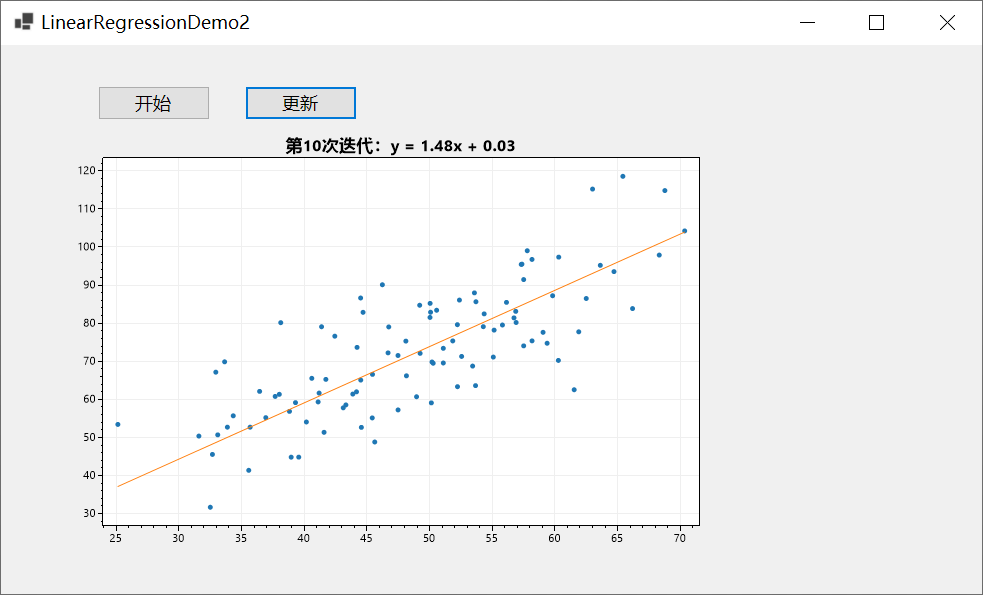
总结
本文以一个控制台应用与一个winform程序为例向大家介绍了C#如何基于ScottPlot进行数据可视化，并介绍了实现动态绘图的两种方式，一种是使用定时器，另一种是使用异步操作，希望对你有所帮助。
C#基于ScottPlot进行可视化的更多相关文章
- 基于Kibana的可视化监控报警插件sentinl入门
sentinl是什么 Kibi/Kibana Alert & Reporting App Watching your data, 24/7/365 sentinl是一个免费的kibana预警与 ...
- 基于flask的可视化动漫分析网站【python入门必学】
课程设计项目名称:基于flask的可视化动漫分析网站,如果你在学习Python的过程中,往往因为没有好的教程或者没人指导从而导致自己容易放弃,为此我建了个Python交流.裙 :一久武其而而流一思(数 ...
- JVM调优（二）——基于JVisualVM的可视化监控
JVM调优(二)--基于JVisualVM的可视化监控 工具路径://java/jdk1.8xxx/bin/JVisuaVM.exe 监控本地的Tomcat 监控远程Tomcat 监控普通的JAVA进 ...
- Visual-platform，基于Vue的可视化大屏开发GUI框架
visual-platform 基于Vue的可视化大屏开发GUI框架 ------ CreatedBy 漆黑小T 构建用于开发可视化大屏项目的自适应布局的GUI框架. github仓库: https: ...
- 性能工具---JConsole基于JMX的可视化监视、管理工具
与visualvm类似: JConsole: (Java Monitoring and Management Console),一种基于JMX的可视化监视.管理工具 VisualVM:(All-in- ...
- [z]Windows 下基于 Eclipse 的可视化远程 Linux C/C++ 开发环境搭建
http://blog.csdn.net/lostaway/article/details/8086056 1.简介 Windows 下远程 Linux 开发工具,比较著名的就是 WinGDB 和 M ...
- 图数据库HugeGraph：HugeGraph-Hubble基于Web的可视化图管理初体验
原创/朱季谦 一.HugeGraph-Hubble简介 关于HugeGraph,官方资料是这样介绍的,它是一款易用.高效.通用的开源图数据库系统(Graph Database), 实现了 Apache ...
- 基于leaflet地图可视化（一）
最近,在学习地图可视化是基于公司的项目.但公司在项目上居然用图片来代替.无语~~~项目效果图(第一版)如下: 突发奇想,2016年自己就接触过地图可视化.但那是没有深入研究.只会用R语言来实现点基础. ...
- 搭建一个基于CentOS的可视化zookeeper管理工具zkUI实现对zk的可视化管理
一. zookeeper 可视化工具 JMX => CLRProfile ZKUI => java写的一个可视化的web网站 github中下载 https://github.com/ ...
- B/S 端构建的基于 WebGL 3D 可视化档案馆管理系统
前言 档案管理系统是通过建立统一的标准以规范整个文件管理,包括规范各业务系统的文件管理的完整的档案资源信息共享服务平台,主要实现档案流水化采集功能.为企事业单位的档案现代化管理,提供完整的解决方案,档 ...
随机推荐
- 【matplotlib 实战】--堆叠面积图
堆叠面积图和面积图都是用于展示数据随时间变化趋势的统计图表,但它们的特点有所不同.面积图的特点在于它能够直观地展示数量之间的关系,而且不需要标注数据点,可以轻松地观察数据的变化趋势.而堆叠面积图则更适 ...
- 前端三件套系例之CSS——响应式布局
文章目录 1.什么是响应式设计 1-1 定义 1-2 响应式设计的优势 2.屏幕的相关概念 3.viewport 视口 3-1 什么是viewport 3-2 设置viewport 4.媒体查询 @m ...
- 在 Rust 中 gRPC 使用的 protobuf 实现条件编译服务器和客户端（tonic）
前言 Rust 中 gRPC 最优秀的库是 tonic.tonic-build 的默认生成方式是生成一个带有数据类型和客户端与服务端源码,而对于分层应用,客户端尽可能不要知道服务端的代码,同时服务端也 ...
- [Python急救站课程]简单的人机对话
一个简单的人机对话程序 name = input("输入姓名:") # input输入数据 print("{}同学,学好Python,前途无量!".format ...
- Ubuntu部署雷池Waf社区版
安装docker环境 更新软件包 sudo apt update 安装docker环境 apt-get install docker.io docker -v 安装docker compose V2版 ...
- 【外包杯】【报错】微信小程序 “［app.json 文件内容错误］app.json：未找到［“pages”］［0］对应 pages/xx/xx.wxml（或其他）文件” 报错 的简单解决方案(已解决)
问题的解决方案 删除components目录下的uni-link文件夹
- AtCoder_abc330
AtCoder_abc330 比赛链接 A - Counting Passes A题链接 题目大意 给出\(N\)个数\(a_1,a_2,a_3\cdots,a_N\),和一个正整数\(L\).输出有 ...
- 初始OpenGL
OpenGL到底是什么? 一般它被认为是一个API,包含一系列操作图形,图像的函数.然而,它并不是一个API,而是Khronos组织制定并维护的规范. OpenGL规定了每个函数如何执行,以及它们的输 ...
- Object.defineProperty用法
1.能干啥? Object.defineProperty()可以给传入的对象动态的添加或修改属性 2.怎么玩? Object.defineProperty(obj,prop,desc)它有三个参数: ...
- C++中数字与字符串之间的转换（转载自http://www.cnblogs.com/luxiaoxun/）
C++中数字与字符串之间的转换 1.字符串数字之间的转换(1)string --> char * string str("OK"); char * p = str ...