神经网络优化篇：详解偏差，方差（Bias /Variance）

偏差，方差

注意到，几乎所有机器学习从业人员都期望深刻理解偏差和方差，这两个概念易学难精，即使自己认为已经理解了偏差和方差的基本概念，却总有一些意想不到的新东西出现。关于深度学习的误差问题，另一个趋势是对偏差和方差的权衡研究甚浅，可能听说过这两个概念，但深度学习的误差很少权衡二者，总是分别考虑偏差和方差，却很少谈及偏差和方差的权衡问题，下面来一探究竟。

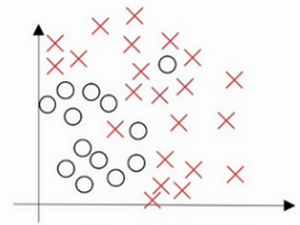
假设这就是数据集，如果给这个数据集拟合一条直线，可能得到一个逻辑回归拟合，但它并不能很好地拟合该数据，这是高偏差（high bias）的情况，称为“欠拟合”（underfitting）。

相反的如果拟合一个非常复杂的分类器，比如深度神经网络或含有隐藏单元的神经网络，可能就非常适用于这个数据集，但是这看起来也不是一种很好的拟合方式分类器方差较高（high variance），数据过度拟合（overfitting）。

在两者之间，可能还有一些像图中这样的，复杂程度适中，数据拟合适度的分类器，这个数据拟合看起来更加合理，称之为“适度拟合”（just right）是介于过度拟合和欠拟合中间的一类。

在这样一个只有\(x_1\)和\(x_2\)两个特征的二维数据集中，可以绘制数据，将偏差和方差可视化。在多维空间数据中，绘制数据和可视化分割边界无法实现，但可以通过几个指标，来研究偏差和方差。

沿用猫咪图片分类这个例子，左边一张是猫咪图片，右边一张不是。理解偏差和方差的两个关键数据是训练集误差（Train set error）和验证集误差（Dev set error），为了方便论证，假设可以辨别图片中的小猫，用肉眼识别几乎是不会出错的。

假定训练集误差是1%，为了方便论证，假定验证集误差是11%，可以看出训练集设置得非常好，而验证集设置相对较差，可能过度拟合了训练集，在某种程度上，验证集并没有充分利用交叉验证集的作用，像这种情况，称之为“高方差”。

通过查看训练集误差和验证集误差，便可以诊断算法是否具有高方差。也就是说衡量训练集和验证集误差就可以得出不同结论。

假设训练集误差是15%，把训练集误差写在首行，验证集误差是16%，假设该案例中人的错误率几乎为0%，人们浏览这些图片，分辨出是不是猫。算法并没有在训练集中得到很好训练，如果训练数据的拟合度不高，就是数据欠拟合，就可以说这种算法偏差比较高。相反，它对于验证集产生的结果却是合理的，验证集中的错误率只比训练集的多了1%，所以这种算法偏差高，因为它甚至不能拟合训练集。

再举一个例子，训练集误差是15%，偏差相当高，但是，验证集的评估结果更糟糕，错误率达到30%，在这种情况下，会认为这种算法偏差高，因为它在训练集上结果不理想，而且方差也很高，这是方差偏差都很糟糕的情况。

再看最后一个例子，训练集误差是0.5%，验证集误差是1%，用户看到这样的结果会很开心，猫咪分类器只有1%的错误率，偏差和方差都很低。

有一点先在这个简单提一下，这些分析都是基于假设预测的，假设人眼辨别的错误率接近0%，一般来说，最优误差也被称为贝叶斯误差，所以，最优误差接近0%，就不在这里细讲了，如果最优误差或贝叶斯误差非常高，比如15%。再看看这个分类器（训练误差15%，验证误差16%），15%的错误率对训练集来说也是非常合理的，偏差不高，方差也非常低。

当所有分类器都不适用时，如何分析偏差和方差呢？比如，图片很模糊，即使是人眼，或者没有系统可以准确无误地识别图片，在这种情况下，最优误差会更高，那么分析过程就要做些改变了，暂时先不讨论这些细微差别，重点是通过查看训练集误差，可以判断数据拟合情况，至少对于训练数据是这样，可以判断是否有偏差问题，然后查看错误率有多高。当完成训练集训练，开始使用验证集验证时，可以判断方差是否过高，从训练集到验证集的这个过程中，可以判断方差是否过高。

以上分析的前提都是假设基本误差很小，训练集和验证集数据来自相同分布，如果没有这些假设作为前提，分析过程更加复杂。

所以偏差和方差都高是什么样子呢？这种情况对于两个衡量标准来说都是非常糟糕的。

之前讲过，这样的分类器，会产生高偏差，因为它的数据拟合度低，像这种接近线性的分类器，数据拟合度低。

但是如果稍微改变一下分类器，它会过度拟合部分数据，这样的分类器具有高偏差和高方差，偏差高是因为它几乎是一条线性分类器，并未拟合数据。

这种二次曲线能够很好地拟合数据。

这条曲线中间部分灵活性非常高，却过度拟合了这两个样本，这类分类器偏差很高，因为它几乎是线性的。

而采用曲线函数或二次元函数会产生高方差，因为它曲线灵活性太高以致拟合了这两个错误样本和中间这些活跃数据。

这看起来有些不自然，从两个维度上看都不太自然，但对于高维数据，有些数据区域偏差高，有些数据区域方差高，所以在高维数据中采用这种分类器看起来就不会那么牵强了。

总结一下，讲了如何通过分析在训练集上训练算法产生的误差和验证集上验证算法产生的误差来诊断算法是否存在高偏差和高方差，是否两个值都高，或者两个值都不高，根据算法偏差和方差的具体情况决定接下来要做的工作。