一维DFT

1 DFT的相关内容

一维DFT的意义：一维信号由若干个不同频率的正余弦信号组合而成；
一维DFT的解决问题：确定输入信号中有多少个周期信号，以及周期信号的幅值、频率、相位值；
一维DFT的原理：
- 通过采样频率fs对原始信号进行离散化，依次计算离散信号与各个基信号的相关性（N为采样点数对应存在N个基信号，每个基信号与离散信号会有一个复数结果）
一维DFT的求取步骤：
1. 设定采样频率fs，对输入信号f(t)进行采样，得到N个采样点，对应的离散化信号记作x[n]，n = [0, 1, ..., N) ;
2. 通过DFT公式计算得到N个匹配对X[k]，k= [0, 1, ..., N)，X[k]代表N个采样点的原始信号中存在着k个周期的的信号分量，即第k+1个基信号；
\[X[k]=Σ_{n=0}^{N-1} x(n){e^{-jA}}=Σ_{n=0}^{N-1} x(n)(cos(A)-jsin(A)), 其中A=2πkn/N.
\]
1. 根据总的采样时长 = N / fs，故对于X[k]≠0时，对应输入信号的频率 f = (k * fs) / N；在k≠0时，幅值为复数X[k]的模除以（N/2），在k=0时，幅值为复数X[k]的模除以 N；相位即为复数X[k]的幅角；
2. 注：因为要满足采样定理 fs ≥ 2f，故只使用频率域的前一半结果，由 f = k*fs/N 可推导；
- 假设，X[2] 的模为不为0, 这说明N个采样点中有2个周期，故每个周期的时长T =N / (2 ** fs) *，即输入信号的频率 f = (2 * fs) / N；

2 DFT计算结果验证

DFT计算公式：

\[X[k]=Σ_{n=0}^{N-1} x(n){e^{-jA}}=Σ_{n=0}^{N-1} x(n)(cos(A)-jsin(A)), 其中A=2πkn/N.
\]

通过numpy中np.fft.fft() 函数验证自己实现的代码是正确的，代码如下

import cmath

import matplotlib.pyplot as plt

import numpy as np

plt.rcParams['font.sans-serif'] = ['SimHei']

plt.rcParams['axes.unicode_minus'] = False

np.set_printoptions(edgeitems=3)

arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])

N = len(arr)

omega = 2 * np.pi / N

mag_ls = []

for k in range(N):

    mag_ls.append(sum([arr[j] * cmath.exp(complex(0, -j * omega * k)) for j in range(N)]))

print(np.array(mag_ls))

# [45.  +0.j    -4.5+12.364j -4.5 +5.363j -4.5 +2.598j -4.5 +0.793j

# -4.5 -0.793j -4.5 -2.598j -4.5 -5.363j -4.5-12.364j]

X = np.fft.fft(arr)

print(X)

# [45.  +0.j    -4.5+12.364j -4.5 +5.363j -4.5 +2.598j -4.5 +0.793j

# -4.5 -0.793j -4.5 -2.598j -4.5 -5.363j -4.5-12.364j]

3 DFT的时频曲线分析

问题：给定一个连续的输入信号 f(t) = 2 + 3 * np.cos(2 * np.pi * 0.2 * t) + 1.5 * np.cos(2 * np.pi * 0.1 * t) ，通过 DFT 来求解输入信号中各个周期函数的幅值、频率、相位值；

思路：参考一维DFT的求取步骤

代码实现：

import matplotlib.pyplot as plt

import numpy as np

fs = 0.5    # 采样频率 HZ

t = np.arange(0, 100, 1 / fs)   # 时间序列，每隔 1/fs 秒采集一次数据，共采集N次

N = len(t)     # 序列的长度

x = 2 + 3 * np.cos(2 * np.pi * 0.2 * t) + 1.5 * np.cos(2 * np.pi * 0.1 * t)

X = np.fft.fft(x)

m = np.abs(X)

Mag = m.copy()

ifft_x = np.fft.ifft(X)

ifft_m = np.abs(ifft_x)

freq = [k * fs / N for k in range(N)]

m[0] /= N

m[1:] /= (N / 2)

print("freq:", freq)

plt.figure()

name = "f(t) = 2 + 3 * cos(2π * 0.2 * t) + 1.5 * np.cos(2π * 0.1 * t)"

plt.subplot(131), plt.plot(t, x, c="b", marker="o")

plt.title(name), plt.xlabel("采样周期 t={} 秒".format(1/fs)), plt.ylabel("输出f(t)")

plt.subplot(132), plt.plot(range(N), Mag, c="g", marker="o"), plt.title("DFT 结果")

plt.title("DFT 结果"), plt.xlabel("基信号N=[0~{})".format(N)), plt.ylabel("基信号对应的幅值")

plt.subplot(133), plt.plot(freq, m, c="r", marker="o"), plt.title("DFT 结果")

plt.title("DFT 结果"), plt.xlabel("信号的频率".format(N)), plt.ylabel("真实幅值")

plt.figure()

plt.subplot(121), plt.plot(t, x, c="b"), plt.title("原始信号")

plt.subplot(122), plt.plot(t, ifft_m, c="g"), plt.title("逆DFT信号")

plt.show()

输出结果：

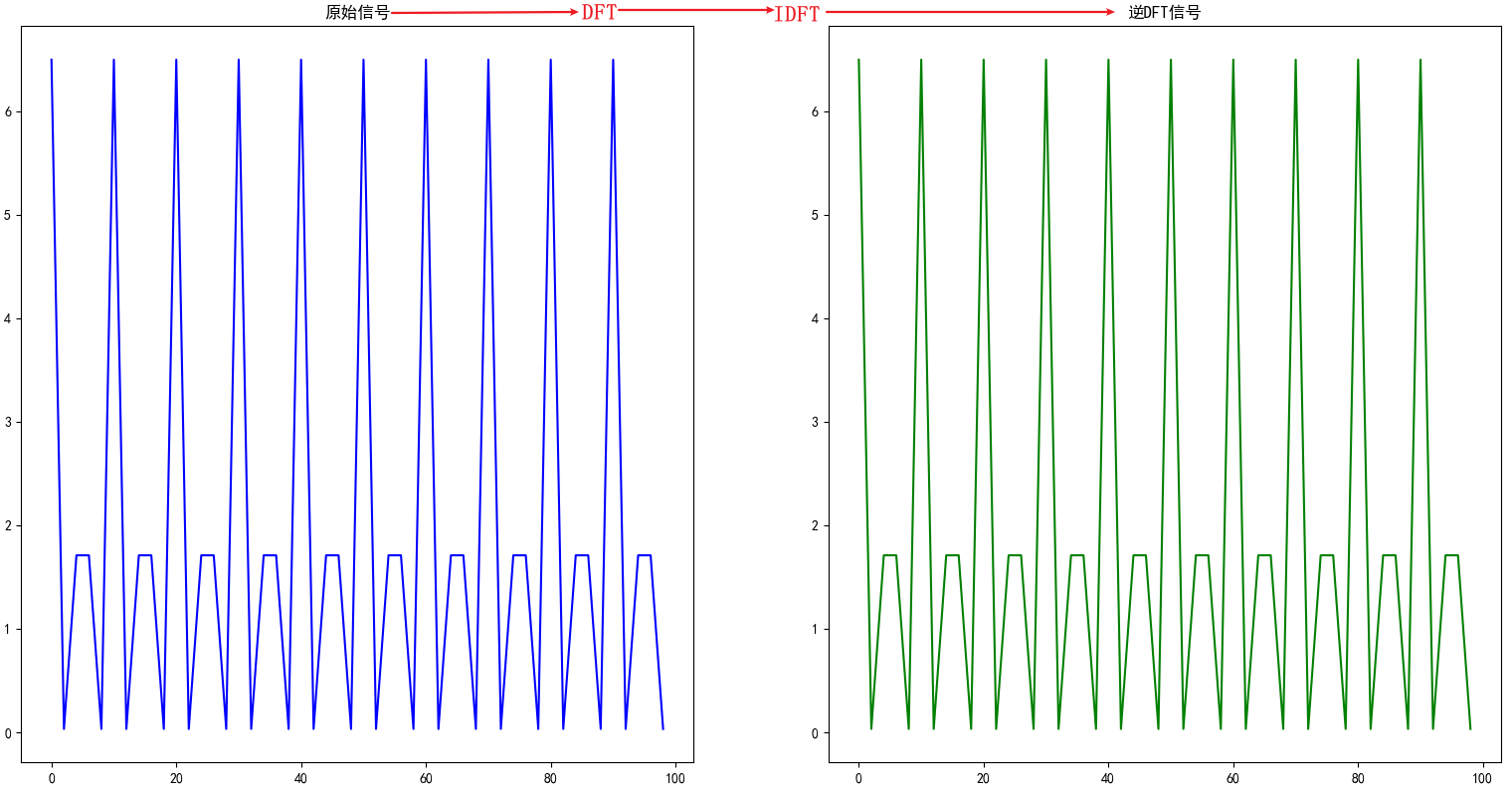
由图1可知：

fs=0.5hz，采样点 N = 50， f = k * fs / N，直流分量的幅值 = X[0] 模 / (50)，其它分量的幅值 = X[k] 模 / (25) k≠0
X[0] 对应输入信号中2，
X[10] 对应输入信号中 1.5 * np.cos(2 * np.pi * 0.1 * t) ，
X[20] 对应输入信号中 3 * np.cos(2 * np.pi * 0.2 * t)

由图2可知，DFT与IDFT是可逆的

4 DFT的应用

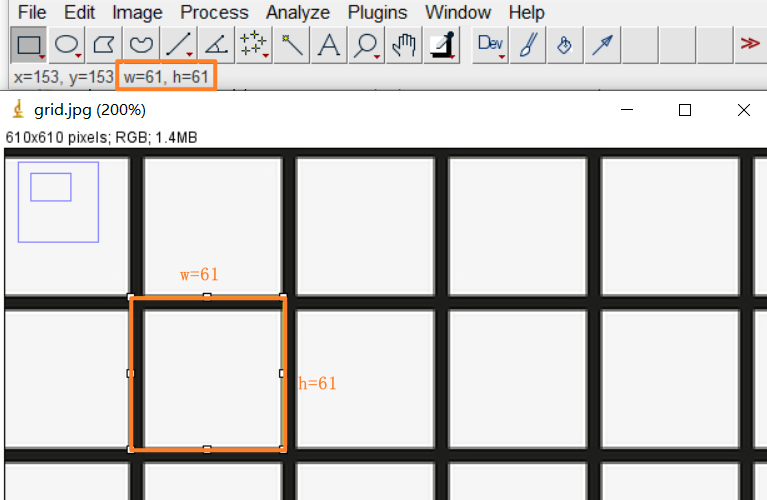
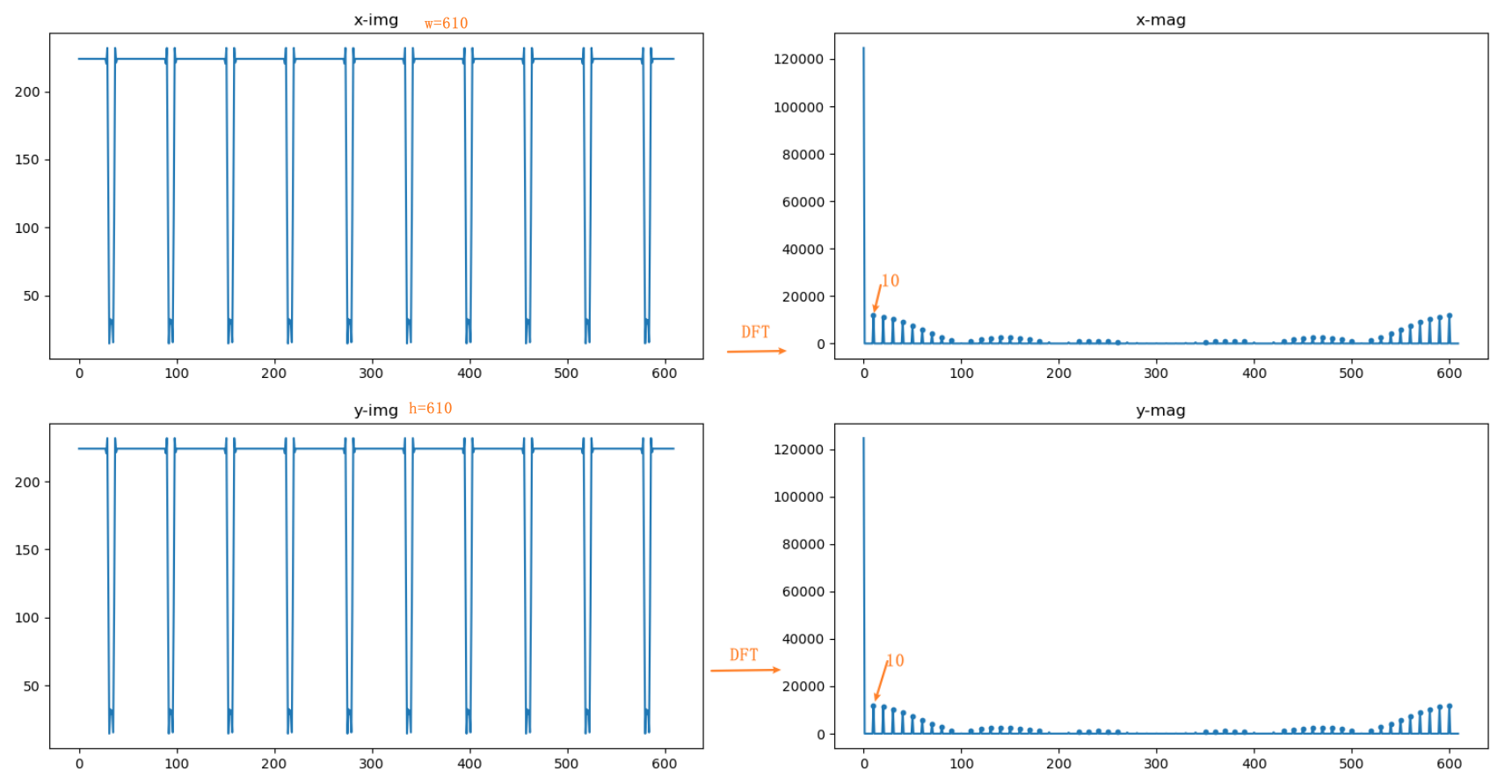
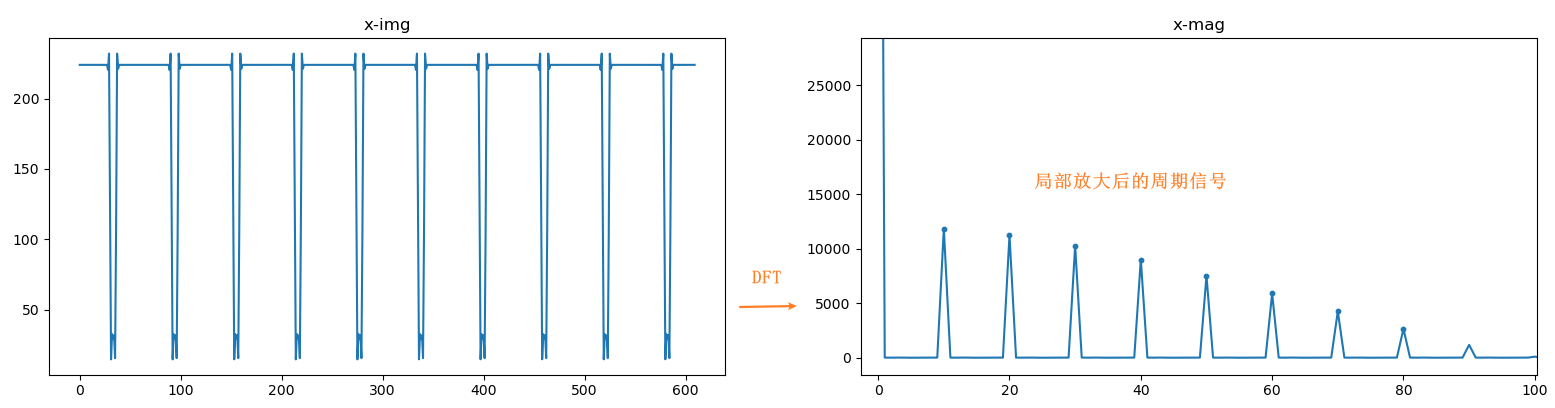
方法：使用DFT求取图像中单个网格的像素大小， psx = 用图像的宽度除以 x方向上网格的数量，psx = 用图像的高度除以 y方向上网格的数量；

思路：求解psx — 在x方向上求取图像的像素均值，然后经过DFT变换，得到频域上的周期信号，其中周期个数即为网格数量；为了缩小误差，可以按照一定大小来缩小图像，重复psx 求取过程，通过平均值来提高计算精度；同理 psy一样。

运行结果：

二维DFT

1 DFT在图像处理时的相关内容

图像中高频与低频区别：
- 高频：变化剧烈的灰度分量，例如边界
- 低频：变化缓慢的灰度分量，例如一片大海
傅里叶变换的作用：滤波、图像配准；
- 低通滤波器：只保留低频，会使得图像模糊
- 高通滤波器：只保留高频，会使得图像细节增强

2 DFT滤波应用

import cv2

import numpy as np

from matplotlib import pyplot as plt

def DFT(image, isshow=True):

    img_float32 = np.float32(image)

    dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)

    dft_shift = np.fft.fftshift(dft)

    # 得到灰度图能表示的形式

    magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))

    if isshow:

        plt.subplot(121), plt.imshow(image, cmap='gray')

        plt.title('Input Image'), plt.xticks([]), plt.yticks([])

        plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')

        plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])

        plt.show()

    return dft_shift

def IDFT(image, dft_shift, Filtter="None", isshow=True):

    if Filtter:

        rows, cols = img.shape

        crow, ccol = int(rows / 2), int(cols / 2)  # 中心位置

        mask = None

        if Filtter == "HIGH":

            # 高通滤波

            mask = np.ones((rows, cols, 2), np.uint8)

            mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 0

        elif Filtter == "LOW":

            # 低通滤波

            mask = np.zeros((rows, cols, 2), np.uint8)

            mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1

        dft_shift = dft_shift * mask

    f_ishift = np.fft.ifftshift(dft_shift)

    img_back = cv2.idft(f_ishift)

    img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])

    if isshow:

        plt.subplot(121), plt.imshow(image, cmap='gray')

        plt.title('Input Image'), plt.xticks([]), plt.yticks([])

        plt.subplot(122), plt.imshow(img_back, cmap='gray')

        plt.title('Result'), plt.xticks([]), plt.yticks([])

        plt.show()

    return img_back

if __name__ == "__main__":

    img = cv2.imread('lena.jpg', 0)

    fshift = DFT(img)

    IDFT(img, fshift, Filtter="LOW")