bzoj 1597 斜率DP

1597: [Usaco2008 Mar]土地购买

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 5115  Solved: 1897
[Submit][Status][Discuss]

Description

农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.

Input

* 第1行: 一个数: N

* 第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽

Output

* 第一行: 最小的可行费用.

Sample Input

4
100 1
15 15
20 5
1 100

输入解释:

共有4块土地.

Sample Output

500

HINT

FJ分3组买这些土地: 第一组:100x1, 第二组1x100, 第三组20x5 和 15x15 plot. 每组的价格分别为100,100,300, 总共500.

---

首先对决策的有序，对土地按照长 x，宽 y 递增排序。

如果：

第一块土地，和第二块土地，第二块土地长宽都要比第一块大，那么第一块就等于不起作用，那么可以不用考虑第一块土地，

于是删掉所有这种不需要考虑的土地，就成了 x 递增，y 递减排列的土地。

这时候，对于前面 i 块土地来说，会可以分成很多部分，要成本最少的一种划分。于是——DP思路就来了。

f[i] 前 i 块土地的最优值。

那么：

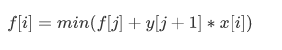
这样O(n^2) 的算法就呼之欲出了，但是，还是会TLE；

怎么办呢？

---

斜率DP：

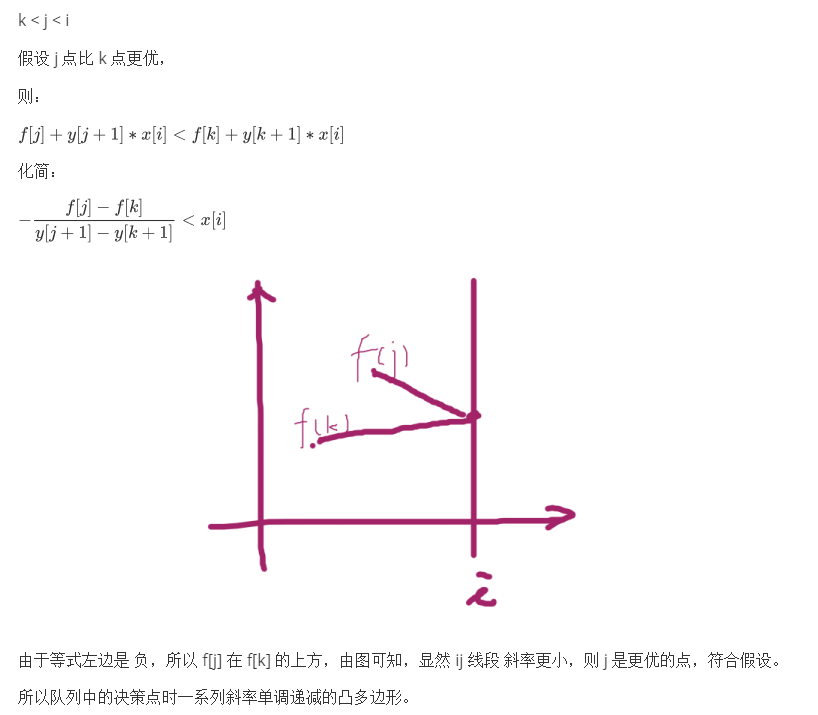
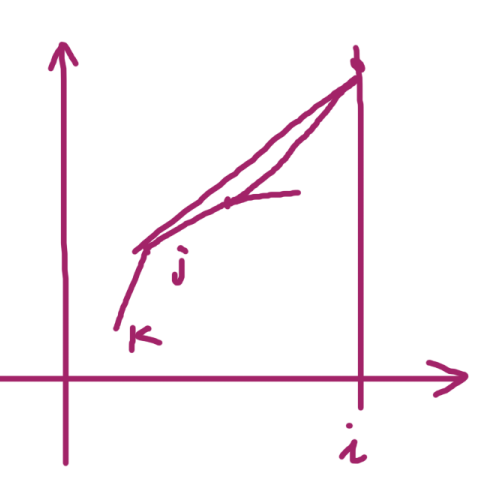
对于 i 点，与之相切的点 斜率才最小，保证 < x[i] ，这个点才是划分点。

到这里，分析就已经完成了，只差队列维护决策点。这个凸多边形了。

就是套路了，

• 考虑凸多边相切的变化规律，找到划分点。
• 用划分点计算新的值。
• 新的值更新凸多边形

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = ;

struct Node
{
    ll x,y;
    bool operator < (const Node& rhs) const {
        if(x==rhs.x) return y < rhs.y;
        return x < rhs.x;
    }
}p[maxn];

ll n,f[maxn],q[maxn];

double slope(long long a,long long b) {
    return (1.0*(f[a]-f[b])/(p[a+].y-p[b+].y));
}

int main(int argc, char const *argv[])
{
    scanf("%I64d",&n);

    for(int i = ; i <= n; i++)
        scanf("%I64d%I64d",&p[i].x,&p[i].y);

    sort(p+,p+n+);

    int cnt = ;
    for(int i = ; i <= n; i++) {
        if(p[i].y<=p[i+].y) continue;
        while(cnt&&p[cnt].y<=p[i].y) --cnt;
        p[++cnt] = p[i];
    }

    int h = ,t = ;
    q[h] = ;

    for(int i = ; i <=cnt; i++) {
        while(t-h>&&slope(q[h],q[h+])>=-p[i].x) ++h;  //删除队首非最优决策点

        f[i] = f[q[h]] + p[q[h]+].y * p[i].x;

        while(t-h>&&slope(q[t-],q[t-])<slope(q[t-],i)) --t;
        q[t++] = i;

    }

    cout<<f[cnt]<<endl;
    return ;
}

参考：http://www.cnblogs.com/akhpl/p/6715148.html