【十大经典数据挖掘算法】EM

【十大经典数据挖掘算法】系列

1. C4.5
2. K-Means
3. SVM
4. Apriori
5. EM
6. PageRank
7. AdaBoost
8. kNN
9. Naïve Bayes
10. CART

---

1. 极大似然

极大似然（Maximum Likelihood）估计为用于已知模型的参数估计的统计学方法。比如，我们想了解抛硬币是正面（head）的概率分布\(\theta\)；那么可以通过最大似然估计方法求得。假如我们抛硬币\(10\)次，其中\(8\)次正面、\(2\)次反面；极大似然估计参数\(\theta\)值：

\[
\hat{\theta} = \arg\underset{\theta}{\max}\, l(\theta) = \arg\underset{\theta}{\max}\, \theta^8(1-\theta)^2
\]

其中，\(l(\theta)\)为观测变量序列的似然函数（likelihood function of the observation sequence）。对\(l(\theta)\)求偏导

\[
\frac{\partial l(\theta)}{\partial \theta} = \theta^7(1-\theta)(8-10\theta) \Rightarrow \hat{\theta} = 0.8
\]

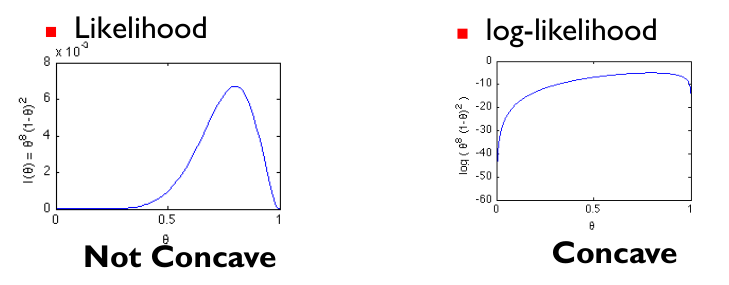
因为似然函数\(l(\theta)\)不是凹函数（concave），求解极大值困难。一般地，使用与之具有相同单调性的log-likelihood，如图所示

凹函数（concave）与凸函数（convex）的定义如图所示：

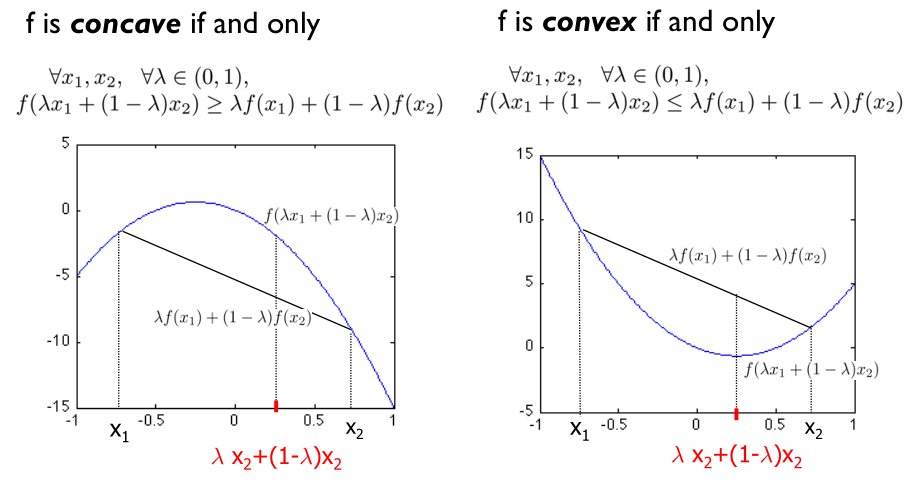
从图中可以看出，凹函数“容易”求解极大值，凸函数“容易”求解极小值。

2. EM算法

EM算法（Expectation Maximization）是在含有隐变量（latent variable）的模型下计算最大似然的一种算法。所谓隐变量，是指我们没有办法观测到的变量。比如，有两枚硬币A、B，每一次随机取一枚进行抛掷，我们只能观测到硬币的正面与反面，而不能观测到每一次取的硬币是否为A；则称每一次的选择抛掷硬币为隐变量。

用Y表示观测数据，Z表示隐变量；Y和Z连在一起称为完全数据( complete-data )，观测数据Y又称为不完全数据(incomplete-data)。观测数据的似然函数：

\[
P(Y | \theta) = \sum_{Z} P(Z|\theta)P(Y|Z,\theta)
\]

求模型参数的极大似然估计：

\[
\hat{\theta} = \arg\underset{\theta}{\max}\, \log P(Y | \theta)
\]

因为含有隐变量，此问题无法求解。因此，Dempster等人提出EM算法用于迭代求解近似解。EM算法比较简单，分为两个步骤：

• E步（E-step），以当前参数\(\theta^{(i)}\)计算\(Z\)的期望值

\[
Q(\theta, \theta^{(i)}) = \mathbb{E}_Z[\log P(Y,X|\theta)| Y, \theta^{(i)}]
\]

• M步（M-step），求使\(Q(\theta, \theta^{(i)})\)极大化的\(\theta\)，确定第\(i+1\)次迭代的参数的估计值\(\theta^{(i+1)}\)

\[
\theta^{(i+1)} = \arg\underset{\theta}{\max}\, Q(\theta, \theta^{(i)})
\]

如此迭代直至算法收敛。关于算法的推导及收敛性证明，可参看李航的《统计学习方法》及Andrew Ng的《CS229 Lecture notes》。这里有一些极大似然以及EM算法的生动例子。

3. 实例

[2]中给出极大似然与EM算法的实例。如图所示，有两枚硬币A、B，每一个实验随机取一枚抛掷10次，共5个实验，我们可以观测到每一次所取的硬币，估计参数A、B为正面的概率\(\theta = (\theta_A, \theta_B)\)，根据极大似然估计求解

如果我们不能观测到每一次所取的硬币，只能用EM算法估计模型参数，算法流程如图所示：

隐变量\(Z\)为每次实验中选择A或B的概率，则第一个实验选择A的概率为

\[
P(z_1 = A |y_1, \theta^{(0)}) = \frac{P(z_1 = A |y_1, \theta^{(0)})}{P(z_1 = A |y_1, \theta^{(0)}) + P(z_1 = B |y_1, \theta^{(0)})} = \frac{0.6^5*0.4^5}{0.6^5*0.4^5 + 0.5^{10}} = 0.45
\]

按照上面的计算方法可依次求出隐变量\(Z\)，然后计算极大化的\(\theta^{(i)}\)。经过10次迭代，最终收敛。

4. 参考资料

[1] 李航，《统计学习方法》.
[2] Chuong B Do & Serafim Batzoglou, What is the expectation maximization algorithm?
[3] Pieter Abbeel, Maximum Likelihood (ML), Expectation Maximization (EM).
[4] Rudan Chen,【机器学习算法系列之一】EM算法实例分析.