[Codeforces1137F]Matches Are Not a Child's Play——LCT+树状数组

题目链接：

[Codeforces1137F]Matches Are Not a Child's Play

题目大意：

我们定义一棵树的删除序列为：每一次将树中编号最小的叶子删掉，将该节点编号加入到当前序列的最末端，最后只剩下一个节点时将该节点的编号加入到结尾。

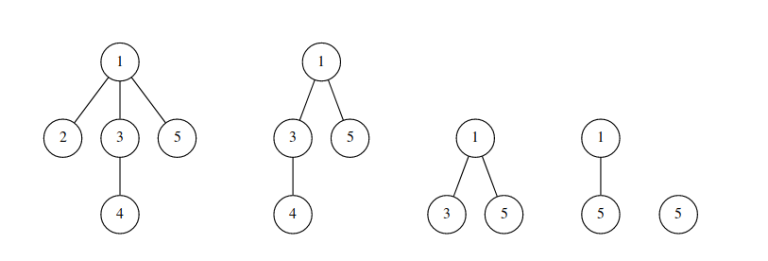
例如对于上图中的树，它的删除序列为：$2\ 4\ 3\ 1\ 5$

现在给出一棵$n$个节点的树，有$m$次操作：

$up\ v$:将$v$号节点的编号变为当前所有节点编号的$max+1$

$when\ v$:查询$v$在当前树的删除序列中是第几号元素

$compare\ u\ v$:查询$u$和$v$在当前树的删除序列中谁更靠前

显然编号最大的点在序列的最后一位(设为$y$)，我们以这个点为根，那么删除就是从下往上删除一段一段的链。

将连续删除的一段链看成是一条重链，整棵树就被分成了若干条重链。

可以发现每条重链的最低端的节点标号是这条重链上最大的。

因为如果要删除链底的那个点，那么说明当前能删除的点都比链底的点大，在删除链底之后一定会连续删除链上的所有点。

现在来考虑一次$up\ x$操作带来的影响：显然最后删除的一定是从$y$到$x$的链，而剩下的点在序列上的相对位置不变。

对于树来说就是将$x$到$y$变成一条重链并将$x$变为根节点。

我们用$LCT$来维护这些重链，对于每条重链按链上的编号最大值来编号，用树状数组来记录每个重链的大小。

$up$操作就相当于$LCT$中的$access$，在$access$时同步修改树状数组上记录的信息即可。

$when$操作就是查重链编号比自己所在重链的编号小的所有重链大小之和及自己所在重链下方的节点数。

$compare$操作就是两个$when$操作。

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<cstdio>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int f[200010];
int s[200010][2];
int size[200010];
int st[200010];
int v[400010];
int tot;
int head[200010];
int nex[400010];
int to[400010];
char ch[10];
int n,m;
int x,y;
int cnt;
int rev[200010];
int val[200010];
void add_edge(int x,int y)
{
    nex[++tot]=head[x];
    head[x]=tot;
    to[tot]=y;
}
void add(int x,int k)
{
    for(int i=x;i<=n+m;i+=i&-i)
    {
        v[i]+=k;
    }
}
int ask(int x)
{
    int res=0;
    for(int i=x;i;i-=i&-i)
    {
        res+=v[i];
    }
    return res;
}
void dfs(int x)
{
    val[x]=x;
    size[x]=1;
    for(int i=head[x];i;i=nex[i])
    {
        if(to[i]!=f[x])
        {
            f[to[i]]=x;
            dfs(to[i]);
            if(val[to[i]]>val[x])
            {
                val[x]=val[to[i]];
                s[x][1]=to[i];
                size[x]=size[to[i]]+1;
            }
        }
    }
    add(val[x],1);
}
bool is_root(int rt)
{
    return rt!=s[f[rt]][0]&&rt!=s[f[rt]][1];
}
bool get(int rt)
{
    return rt==s[f[rt]][1];
}
void pushup(int rt)
{
    size[rt]=size[s[rt][0]]+size[s[rt][1]]+1;
}
void pushdown(int rt)
{
    if(rev[rt])
    {
        swap(s[rt][0],s[rt][1]);
        rev[s[rt][0]]^=1;
        rev[s[rt][1]]^=1;
        rev[rt]=0;
    }
    if(s[rt][0])val[s[rt][0]]=val[rt];
    if(s[rt][1])val[s[rt][1]]=val[rt];
}
void rotate(int rt)
{
    int fa=f[rt];
    int anc=f[fa];
    int k=get(rt);
    if(!is_root(fa))
    {
        s[anc][get(fa)]=rt;
    }
    s[fa][k]=s[rt][k^1];
    f[s[rt][k^1]]=fa;
    s[rt][k^1]=fa;
    f[fa]=rt;
    f[rt]=anc;
    pushup(fa);
    pushup(rt);
}
void splay(int rt)
{
    int top=0;
    st[++top]=rt;
    for(int i=rt;!is_root(i);i=f[i])
    {
        st[++top]=f[i];
    }
    for(int i=top;i>=1;i--)
    {
        pushdown(st[i]);
    }
    for(int fa;!is_root(rt);rotate(rt))
    {
        if(!is_root(fa=f[rt]))
        {
            rotate(get(fa)==get(rt)?fa:rt);
        }
    }
}
void access(int rt)
{
    for(int x=0;rt;x=rt,rt=f[rt])
    {
        splay(rt);
        s[rt][1]=0;
        pushup(rt);
        add(val[rt],-size[rt]);
        add(cnt,size[rt]);
        s[rt][1]=x;
        pushup(rt);
    }
}
void reverse(int rt)
{
    cnt++;
    access(rt);
    splay(rt);
    rev[rt]^=1;
    val[rt]=cnt;
}
int query(int rt)
{
    splay(rt);
    return ask(val[rt])-size[s[rt][0]];
}
int main()
{
    scanf("%d%d",&n,&m);
    cnt=n;
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        add_edge(x,y);
        add_edge(y,x);
    }
    dfs(n);
    for(int i=1;i<=m;i++)
    {
        scanf("%s",ch);
        if(ch[0]=='u')
        {
            scanf("%d",&x);
            reverse(x);
        }
        else if(ch[0]=='w')
        {
            scanf("%d",&x);
            printf("%d\n",query(x));
        }
        else
        {
            scanf("%d%d",&x,&y);
            printf("%d\n",query(x)<query(y)?x:y);
        }
    }
}