P1251 餐巾计划问题 网络流

P1251 餐巾计划问题

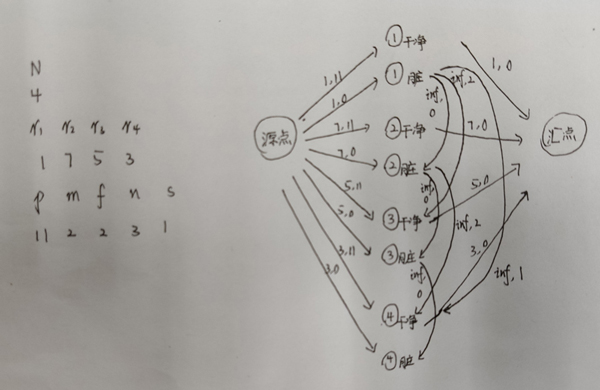
 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = , inf = 0x3f3f3f3f;
 struct Edge {
     int from, to;
     ll cap, flow, cost;
 };
 
 struct MCMF {
     int n, m, s, t;
     vector<Edge> edges;
     vector<int> G[maxn];
     int inq[maxn];
     ll d[maxn];
     int p[maxn];
     ll a[maxn];
 
     void init(int n) {
         this->n = n;
         for (int i = ; i <= n; ++i) G[i].clear();
         edges.clear();
     }
 
     void AddEdge(int from, int to, ll cap, ll cost) {
         edges.push_back((Edge){from, to, cap, , cost});
         edges.push_back((Edge){to, from, , , -cost});
         m = edges.size();
         G[from].push_back(m-);
         G[to].push_back(m-);
     }
     bool BellmanFord(int s, int t, ll& flow, ll& cost) {
         for (int i = ; i <= n; ++i) d[i] = inf;
         memset(inq, , sizeof(inq));
         d[s] = ; inq[s] = ; p[s] = ; a[s] = inf;
 
         queue<int> que;
         que.push(s);
         while (!que.empty()) {
             int u = que.front(); que.pop();
             inq[u] = ;
             for (int i = ; i < G[u].size(); ++i) {
                 Edge& e = edges[G[u][i]];
                 if (e.cap > e.flow && d[e.to] > d[u] + e.cost) {
                     d[e.to] = d[u] + e.cost;
                     p[e.to] = G[u][i];
                     a[e.to] = min(a[u], e.cap-e.flow);
                     if (!inq[e.to]) { que.push(e.to); inq[e.to] = ; }
                 }
             }
         }
         if (d[t] == inf) return false;
         flow += a[t];
         cost += d[t] * a[t];
         int u = t;
         while (u != s) {
             edges[p[u]].flow += a[t];
             edges[p[u]^].flow -= a[t];
             u = edges[p[u]].from;
         }
         return true;
     }
     ll mincost(int s, int t) {
         ll flow = , cost = ;
         while (BellmanFord(s, t, flow, cost));
         return cost;
     }
 }mcmf;
 int r[maxn];
 int main() {
     int N; scanf("%d",&N);
     for (int i = ; i <= N; ++i) {
         scanf("%d",&r[i]);
     }
     int p, m, f, n, s;
     scanf("%d%d%d%d%d",&p,&m,&f,&n,&s);
 
     /// i为干净餐巾量，i+N为脏餐巾量
     int be = *N+, ed = *N+;
     mcmf.init(*N+);
     for (int i = ; i <= N; ++i) {
         /// 通过购买来获得干净餐巾
         mcmf.AddEdge(be,i,r[i],p);
         /// 当天的脏餐巾如何使用
         mcmf.AddEdge(be,i+N,r[i],);
         /// 当天的脏餐巾留到明天
         if (i+ <= N) mcmf.AddEdge(i+N,(i+)+N,inf,);
         /// 通过快洗部洗脏餐巾
         if (i+m <= N) mcmf.AddEdge(i+N,i+m,inf,f);
         /// 通过慢洗部洗脏餐巾
         if (i+n <= N) mcmf.AddEdge(i+N,i+n,inf,s);
         /// 使用当天的干净餐巾
         mcmf.AddEdge(i,ed,r[i],);
     }
     ll ans = mcmf.mincost(be,ed);
     printf("%lld\n",ans);
     return ;
 }