[hdu5323]复杂度计算，dfs

题意：求最小的线段树的右端点（根节点表示区间[0,n]），使得给定的区间[L,R]是线段树的某个节点。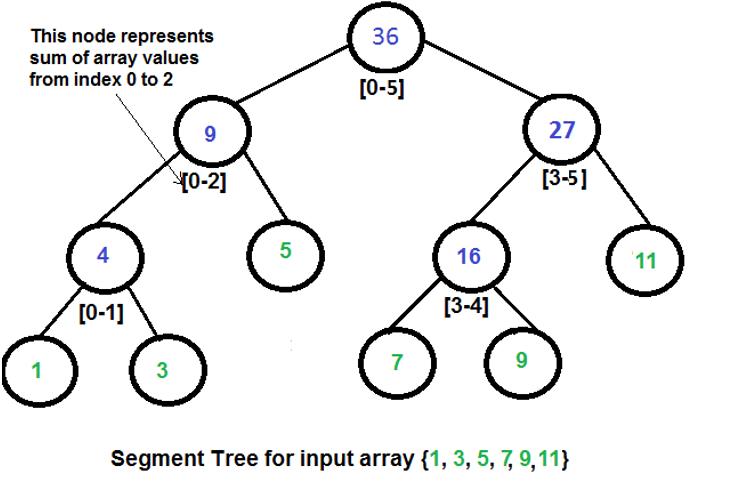

数据范围：L,R<=1e9,L/(R-L+1)<=2015

思路：首先从答案出发来判断是否出现给定区间是行不通的，于是只能从[L,R]出发来寻找答案。如果一个子节点表示区间[L,R]，那么它的父节点可能是四种表示方式之一，分别是[L,2R-L],[L,2R-L+1],[2L-R-1,R],[2L-R-2,R]，其中父节点为[L,2R-L]时要求R>L，否则它的右儿子就为空了，这是不允许的。接下来看无解的条件，如果L<(R-L+1)了，那么就是无解的，因为左儿子不可能比右儿子表示的区间长度小，也就是说L/(R-L+1)小于1时就可以判定为无解了。注意到由儿子节点到父亲节点，(R-L+1)变为了原来的两倍左右，而L是非增的，所以L/(R-L+1)每经过一层，值变为原来的1/2左右，有题目给定的数据，L/(R-L+1)<=2015，所以层数最多只有log₂²⁰¹⁵=11，这不难想到dfs暴力扩展了，dfs总共只会扩展出4^11=4000000个节点，可以承受。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67

/* ******************************************************************************** */ #include <iostream>                                                                 // #include <cstdio>                                                                   // #include <cmath>                                                                    // #include <cstdlib>                                                                  // #include <cstring>                                                                  // #include <vector>                                                                   // #include <ctime>                                                                    // #include <deque>                                                                    // #include <queue>                                                                    // #include <algorithm>                                                                // using namespace std;                                                                //                                                                                     // #define pb push_back                                                                // #define mp make_pair                                                                // #define X first                                                                     // #define Y second                                                                    // #define all(a) (a).begin(), (a).end()                                               // #define foreach(i, a) for (typeof(a.begin()) it = a.begin(); it != a.end(); it ++)  //                                                                                     // void RI(vector<int>&a,int n){a.resize(n);for(int i=0;i<n;i++)scanf("%d",&a[i]);}    // void RI(){}void RI(int&X){scanf("%d",&X);}template<typename...R>                    // void RI(int&f,R&...r){RI(f);RI(r...);}void RI(int*p,int*q){int d=p<q?1:-1;          // while(p!=q){scanf("%d",p);p+=d;}}void print(){cout<<endl;}template<typename T>      // void print(const T t){cout<<t<<endl;}template<typename F,typename...R>              // void print(const F f,const R...r){cout<<f<<", ";print(r...);}template<typename T>   // void print(T*p, T*q){int d=p<q?1:-1;while(p!=q){cout<<*p<<", ";p+=d;}cout<<endl;}   //                                                                                     // typedef pair<int, int> pii;                                                         // typedef long long ll;                                                               // typedef unsigned long long ull;                                                     //                                                                                     // /* -------------------------------------------------------------------------------- */                                                                                     // template<typename T>bool umax(T &a, const T &b) {     return a >= b? false : (a = b, true); }   ll ans, L, R;   void dfs(ll L, ll R) {     if (L == 0) {         if (ans == -1 || ans > R) ans = R;         return ;     }     ll s = L, t = R - L + 1;     if (s < t) return ;     if (L < R) dfs(L, 2 * R - L);     dfs(L, 2 * R - L + 1);     dfs(2 * L - R - 1, R);     dfs(2 * L - R - 2, R); } int main() { #ifndef ONLINE_JUDGE     freopen("in.txt", "r", stdin); #endif // ONLINE_JUDGE     while (cin >> L >> R) {         ans = -1;         dfs(L, R);         cout << ans << endl;     }     return 0;                                                                       // }                                                                                   //                                                                                     //                                                                                     //                                                                                     // /* ******************************************************************************** */