【NOI2018】你的名字（SAM & 线段树合并）

Description

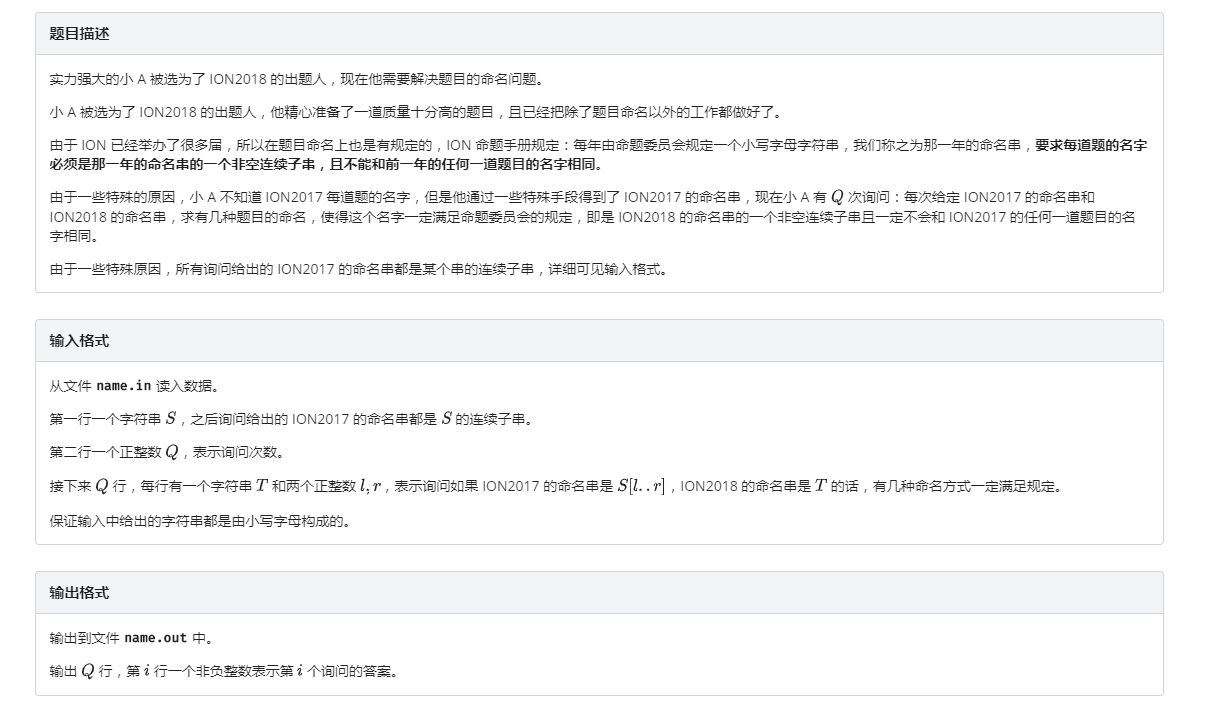
Hint

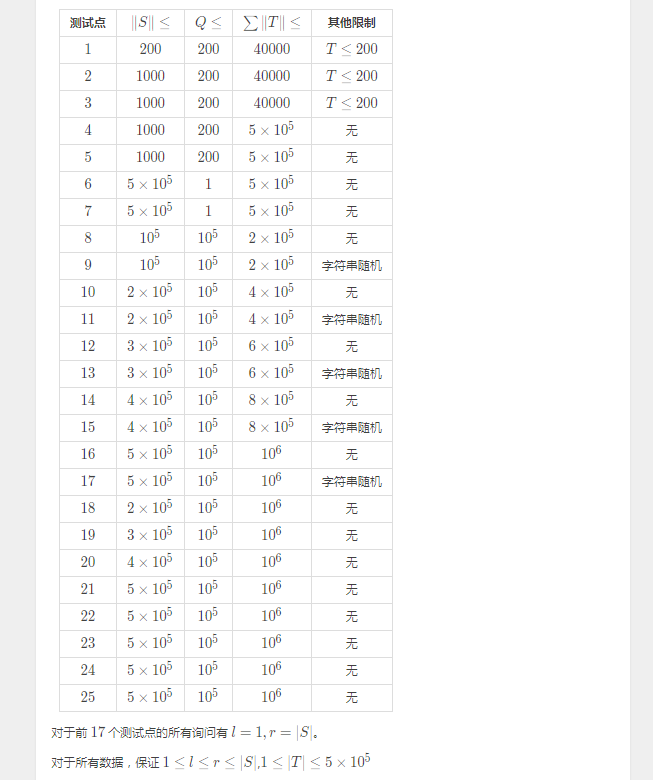
Solution

不妨先讨论一下无区间限制的做法。

首先“子串”可以理解为“前缀的后缀”，因此我们定义一个 \(\lim(i)\)，表示 \(T\) 的一个前缀 \(T[1\cdots i]\) 中，选取一个最长后缀，使得这个后缀在 \(S\) 中出现过。\(\lim(i)\) 就是这个最长后缀的长度。

其实与朴素的 SAM 求最长公共子串有点相似，这里主要是求 本质不同的公共子串的个数。

我们对 \(S\) 建 SAM，然后把 \(T\) 放到 \(S\) 上跑。如果存在转移，那么直接走，当前匹配长度加一；反之就退而求其次。

计算出 \(\lim\) 后，我们发现，对于 \(T\) 的一个前缀的所有后缀，长度不超过 \(\lim\) 的都在主串中出现过。

因为需要去重，所以对询问串 \(T\) 也需要建 SAM。于是不难写出答案的计算公式： \(\text{ans} = \sum\limits_{x\in Q(\text{SAM of } T)} \max(\text{len}(x) - \max(\text{len}(\text{len}(x), \lim(\text{len}(\text{dir}(x)))), 0)\)

简单解释一下：对于 \(T\) 的 SAM 中的结点 \(x\)，原来是有 \(\text{len}(x) - \text{len}(\text{link}(x))\) 的贡献的，然而我们多了一个 \(\lim\) 的限制，于是我们将减数取最大值。而 \(\text{dir}\) 表示当前结点在构造 SAM 时，拆点是从哪个点拆出来的。如果并不是拆点新建的点则 \(\text{dir}(x) = x\)。实际上，\(\text{len}(\text{dir}(x))\) 即为 第一次出现的结尾位置。

---

接下来讨论如何应付区间限制。

这就需要维护 \(\text{end-pos}\) 集合。那么在转移前还需判断，下一个结点是否在 \(S[l + \text{len}\cdots r]\) 内。(\(\text{len}\) 表示当前的匹配长度)

于是我们需要一种可靠的 DS 来维护这个 \(\text{end-pos}\) 集，支持查找其中是否含有在某个值域中的元素。

我们注意到，\(\text{end-pos}\) 的关系可以构成一个 树形结构，因此可以向根的方向将集合合并。也就是说还需要高效的合并。

其实用 线段树合并 来做是维护整个 \(\text{end-pos}\) 是常用套路。为了合并时不破坏原有的信息，我们应在过程中新建结点（类似于可持久化）。

---

回归走转移的过程。

加上线段树，也许会这么写：

void trans(int& x, int& len, int l, int r, int c) {
	for (; ; len = MS[MS[x].link].len, x = MS[x].link) {
		if (MS[x].ch[c] && segt::find(MS[MS[x].ch[c]].eprt, l + len, r)) {
			++len, x = MS[x].ch[c];
			break;
		}
		if (x == 1) break;
	}
}

但这样只有 96 pts。正确的写法应该是 逐步减小 这个 len，因为此时线段树的搜索区间不断增大，期间可能出现满足条件的情况，导致还没有跳后缀链接时就可以跳出。

附上满分的写法：

void trans(int& x, int& len, int l, int r, int c) {
	while (true) {
		if (MS[x].ch[c] && segt::find(MS[MS[x].ch[c]].eprt, l + len, r)) {
			++len, x = MS[x].ch[c];
			break;
		}
		if (!len) break;
		if (MS[MS[x].link].len == --len) x = MS[x].link; // 逐步减小
	}
}

---

时空复杂度：\(O(n\log n)\)，这里 \(\Sigma = 26\) 视为常数。

Code

/*
 * Author : _Wallace_
 * Source : https://www.cnblogs.com/-Wallace-/
 * Problem : NOI2018 你的名字
 */
#include <algorithm>
#include <cctype>
#include <cstring>
#include <cstdio>
#include <map>

using namespace std;
const int N = 5e5 + 5;
int n, q;

namespace io {
	// fast io - by cyjian
    const int __SIZE = (1 << 21) + 1;
    char ibuf[__SIZE], *iS, *iT, obuf[__SIZE], *oS = obuf, *oT = oS + __SIZE - 1, __c, qu[55]; int __f, qr, _eof;
    #define Gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, __SIZE, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
    inline void flush () { fwrite (obuf, 1, oS - obuf, stdout), oS = obuf; }
    inline void gc (char &x) { x = Gc(); }
    inline void pc (char x) { *oS ++ = x; if (oS == oT) flush (); }
    inline void pstr (const char *s) { int __len = strlen(s); for (__f = 0; __f < __len; ++__f) pc (s[__f]); }
    inline void gstr (char *s) { for(__c = Gc(); __c < 32 || __c > 126 || __c == ' ';)  __c = Gc();
        for(; __c > 31 && __c < 127 && __c != ' ' && __c != '\n' && __c != '\r'; ++s, __c = Gc()) *s = __c; *s = 0; }
    template <class I> inline bool gi (I &x) { _eof = 0;
        for (__f = 1, __c = Gc(); (__c < '0' || __c > '9') && !_eof; __c = Gc()) { if (__c == '-') __f = -1; _eof |= __c == EOF; }
        for (x = 0; __c <= '9' && __c >= '0' && !_eof; __c = Gc()) x = x * 10 + (__c & 15), _eof |= __c == EOF; x *= __f; return !_eof; }
    template <class I> inline void print (I x) { if (!x) pc ('0'); if (x < 0) pc ('-'), x = -x;
        while (x) qu[++ qr] = x % 10 + '0',  x /= 10; while (qr) pc (qu[qr --]); }
    struct Flusher_ {~Flusher_(){flush();}}io_flusher_;
};

namespace segt {
	const int S = N << 6;
	int lc[S], rc[S], total(0);
	#define mid ((l + r) >> 1)
	void insert(int& x, int p, int l = 1, int r = n) {
		if (!x) x = ++total;
		if (l == r) return;
		if (p <= mid) insert(lc[x], p, l, mid);
		else insert(rc[x], p, mid + 1, r);
	}
	int merge(int x, int y) {
		if (!x || !y) return x | y;
		int z = ++total;
		lc[z] = merge(lc[x], lc[y]);
		rc[z] = merge(rc[x], rc[y]);
		return z;
	}
	bool find(int& x, int a, int b, int l = 1, int r = n) {
		if (!x) return false;
		if (a <= l && r <= b) return true;
		if (a <= mid && find(lc[x], a, b, l, mid)) return true;
		if (b > mid && find(rc[x], a, b, mid + 1, r)) return true;
		return false;
	}
}; // namespace segt

int b[N << 1], c[N];
template<int N, bool F> struct SAM {
	struct Node {
		int ch[26];
		int link, len, eprt, dir;
	} t[N << 1];
	int total, last;

	void extend(int c) {
		int p = last, np = last = ++total;
		t[np].len = t[p].len + 1, t[np].dir = np;
		for (; p && !t[p].ch[c]; p = t[p].link)
			t[p].ch[c] = np;
		if (!p) {
			t[np].link = 1;
		} else {
			int q = t[p].ch[c];
			if (t[q].len == t[p].len + 1) {
				t[np].link = q;
			} else {
				int nq = ++total;
				t[nq] = t[q], t[nq].len = t[p].len + 1;
				t[np].link = t[q].link = nq;
				for (; p && t[p].ch[c] == q; p = t[p].link)
					t[p].ch[c] = nq;
			}
		}
		if (F) segt::insert(t[np].eprt, t[np].len);
	}
	void init(char* s) {
		if (!F) fill(t, t + 1 + total, Node());
		last = total = 1;
		for (register int i = 0; s[i]; i++) extend(s[i] - 'a');
		if (!F) return;
		for (register int i = 1; i <= total; i++) ++c[t[i].len];
		for (register int i = 1; i <= total; i++) c[i] += c[i - 1];
		for (register int i = 1; i <= total; i++) b[c[t[i].len]--] = i;
		for (register int i = total; i; i--)
			t[t[b[i]].link].eprt = segt::merge(t[b[i]].eprt, t[t[b[i]].link].eprt);
	}
	Node& operator [] (int p) {
		return t[p];
	}
}; // struct SAM

SAM<N, true> MS;
SAM<N << 1, false> QS;

void trans(int& x, int& len, int l, int r, int c) {
	while (true) {
		if (MS[x].ch[c] && segt::find(MS[MS[x].ch[c]].eprt, l + len, r)) {
			++len, x = MS[x].ch[c];
			break;
		}
		if (!len) break;
		if (MS[MS[x].link].len == --len) x = MS[x].link;
	}
}

int lim[N];
long long solve(char* s, int l, int r) {
	int x = 1;
	for (register int i = 1; s[i - 1]; i++) {
		int c = s[i - 1] - 'a';
		lim[i] = lim[i - 1];
		trans(x, lim[i], l, r, c);
	}

	QS.init(s);
	long long ans = 0ll;
	for (register int i = 2; i <= QS.total; i++) {
		int tmp = QS[i].len - max(QS[QS[i].link].len, lim[QS[QS[i].dir].len]);
		ans += (tmp > 0) ? tmp : 0;
	}
	return ans;
}

char s[N << 1];
signed main() {
	freopen("name.in", "r", stdin);
	freopen("name.out", "w", stdout);

	io::gstr(s);
	n = strlen(s);
	MS.init(s);

	io::gi(q);
	while (q--) {
		int l, r;
		io::gstr(s), io::gi(l), io::gi(r);
		io::print(solve(s, l, r));
		io::pc('\n');
	}
	return 0;
}