BehaviorTree.CPP行为树BT的选择节点（四）

Fallback

该节点家族在其他框架中被称为“选择器Selector”或“优先级Priority”。

他们的目的是尝试不同的策略，直到找到可行的策略。

它们具有以下规则：

• tick第一个孩子之前，节点状态为RUNNING。
• 如果子节点返回FAILURE,则后备会tick下一个节点。
• 如果最后一个子节点也返回FAILURE，则所有子节点都将暂停，并且序列将返回FAILURE。
• 如果子节点返回SUCCESS，它将停止并返回SUCCESS。 所有的子节点都停止了。

当孩子返回RUNNING时，Fallback的两个版本的反应方式不同：

• FallbackStar将返回RUNNING，并且下次对其进行tick时，它将在之前停止的那个节点上tick。
• 普通的旧Fallback会返回RUNNING，并且每次执行后都会重置下一个要执行的子级的索引。

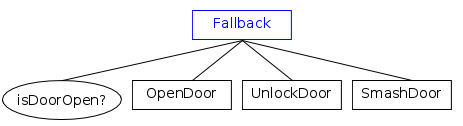
Fallback

在此示例中，我们尝试不同的策略来打开大门。 首先（和一次）检查门是否打开。

// index is initialized to 0 in the constructor
status = RUNNING;

while( _index < number_of_children )
{
    child_status = child[index]->tick();

    if( child_status == RUNNING ) {
        // Suspend execution and return RUNNING.
        // At the next tick, _index will be the same.
        return RUNNING;
    }
    else if( child_status == FAILURE ) {
        // continue the while loop
        _index++;
    }
    else if( child_status == SUCCESS ) {
        // Suspend execution and return SUCCESS.
        HaltAllChildren();
        _index = 0;
        return SUCCESS;
    }
}
// all the children returned FAILURE. Return FAILURE too.
index = 0;
HaltAllChildren();
return FAILURE;

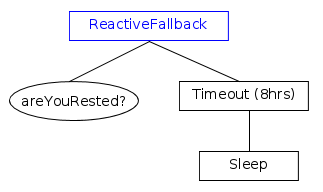
ReactiveFallback

如果先前条件之一将其状态从FAILURE更改为SUCCESS，则当您想中断异步子项时，将使用此ControlNode：ReactiveFallback。

在以下示例中，如果角色充分休息，则该角色最多可睡8个小时或更短的时间。

伪代码

// index is initialized to 0 in the constructor
status = RUNNING;

for (int index=0; index < number_of_children; index++)
{
    child_status = child[index]->tick();

    if( child_status == RUNNING ) {
        return RUNNING;
    }
    else if( child_status == FAILURE ) {
        // continue the while loop
        index++;
    }
    else if( child_status == SUCCESS ) {
        // Suspend execution and return SUCCESS.
        // At the next tick, index will be the same.
        HaltAllChildren();
        return SUCCESS;
    }
}
// all the children returned FAILURE. Return FAILURE too.
index = 0;
HaltAllChildren();
return FAILURE;

原文