模糊C均值算法

Fuzzy C-Means读书笔记

一、算法简介

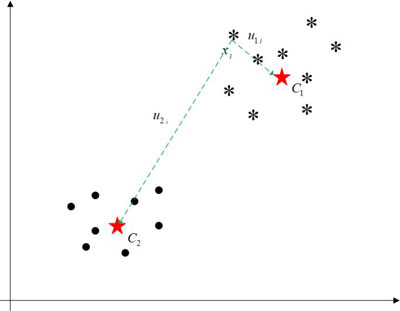
很显然，图中的数据集可分为两个簇。借鉴K-Means算法的思想，利用单个特殊的点(质心)表示一个簇。因此，我们用\(C_1\)和\(C_2\)分别表示簇1和簇2。现在我们将隶属度引入到K-Means中，这就是我们研究的模糊C-Means算法。

二、算法的目标函数

K-Means算法的评价指标：簇内样本之间的距离尽可能的小，簇间样本之间的距离尽可能的大。Fuzzy C-Means继承并发展了它的评价指标。在K-Means算法中，每个数据只能归属一个簇。而在Fuzzy C-Means算法中，每个数据归属C个类。例如，在上图中，第\(j\)个数据\(x_j\)与\(C_1\)和\(C_2\)的距离分别为\(||x_j - C_1||^2\)、\(||x_j - C_2||^2\)。由上图可知，\(x_j\)属于\(C_1\)。所以我们希望\(||x_j - C_1||^2\)比\(||x_j - C_2||^2\)更有用点。最简单的想法是引入权重，希望\(u_{1j}\)越大越好，\(u_{2j}\)越小越好。因此，我用使用\(u_{1j}+u_{2j}=1\)对目标函数\((u_{1j})^m||x_j - C_1||^2+(u_{2j})^m||x_j - C_2||^2\)进行约束。模糊指数\(m(m>1)\)控制距离重要性的大小。

假设我们有\(N\)个数据，那么这\(N\)个数据到第一类的距离为：

\[\sum_{j=1}^{N}{(u_{1j})^m||x_j - C_1||^2}
\]

\(N\)个数据到第二类的距离为：

\[\sum_{j=1}^{N}{(u_{1j})^m||x_j - C_2||^2}
\]

则Fuzzy C-Means的目标函数：

\[J = \sum_{i=1}^{2}\sum_{j=1}^{N}{(u_{ij})^m||x_j - C_i||^2}=\sum_{j=1}^{N}{(u_{1j})^m||x_j - C_1||^2} + \sum_{j=1}^{N}{(u_{1j})^m||x_j - C_2||^2} \\
s.t.
\left\{
\begin{matrix}
\sum_{i=1}^{2}{u_{i1}}=u_{11}+u_{21}=1\\
\sum_{i=1}^{2}{u_{i2}}=u_{11}+u_{22}=1\\
...\\
\sum_{i=1}^{2}{u_{iN}}=u_{1N}+u_{2N}=1
\end{matrix}
\right.
\]

三、算法迭代公式推导

这里，我们对上述的目标函数中的类别数2扩展到任意数\(L\)，即

\[J = \sum_{i=1}^{L}\sum_{j=1}^{N}{(u_{ij})^m||x_j - C_i||^2}\\
s.t.\ \ \ \ \sum_{i=1}^{L}{u_{ij}=1},\ \ \text{j=1,2,...,N}
\]

很显然，拉格朗日乘子法（Lagrange multipliers）是我们求解多元函数在一组约束下的极值的方法。

\[J(u_{ij},C_{i},\lambda_{j}) = \sum_{i=1}^{L}\sum_{j=1}^{N}{(u_{ij})^m||x_j - C_i||^2}+\lambda_{1}(\sum_{i=1}^{L}{u_{i1}}-1)+\lambda_{2}(\sum_{i=1}^{L}{u_{i2}}-1)+...+\lambda_{N}(\sum_{i=1}^{L}{u_{iN}}-1)\\
=\sum_{i=1}^{L}\sum_{j=1}^{N}{(u_{ij})^m||x_j - C_i||^2}+\sum_{j=1}^{N}\lambda_{j}(\sum_{i=1}^{L}{u_{ij}}-1)\\
=\sum_{i=1}^{L}\sum_{j=1}^{N}{(u_{ij})^m||x_j - C_i||^2}+\sum_{j=1}^{N}(\sum_{i=1}^{L}{\lambda{j}u_{ij}}-\lambda_{j})
\]

\(J\)对\(u_{ij}\)求偏导：

\[\frac{\partial{J}}{\partial{u_{ij}}}=mu_{ij}^{m-1}||x_j - C_i||^2+\lambda_{j}=0\\
mu_{ij}^{m-1}||x_j - C_i||^2=-\lambda_{j}\\
u_{ij}^{m-1}=\frac{-\lambda_{j}}{m||x_j - C_i||^2}\\
u_{ij}=(\frac{-\lambda_{j}}{m||x_j - C_i||^2})^{\frac{1}{m-1}}\\
u_{ij}=(-\frac{\lambda_{j}}{m})^{\frac{1}{m-1}}{\frac{1}{||x_j - C_i||^{\frac{2}{m-1}}}}
\]

将上式求出来的\(u_{ij}\)带入约束条件中：

\[1=\sum_{i=1}^{L}u_{ij}=\sum_{i=1}^{L}(-\frac{\lambda_{j}}{m})^{\frac{1}{m-1}}{\frac{1}{||x_j - C_i||^{\frac{2}{m-1}}}}\\
1=(-\frac{\lambda_{j}}{m})^{\frac{1}{m-1}}\sum_{i=1}^{L}{\frac{1}{||x_j - C_i||^{\frac{2}{m-1}}}}\\
(-\frac{\lambda_{j}}{m})^{\frac{1}{m-1}}=\frac{1}{\sum_{i=1}^{L}{\frac{1}{||x_j - C_i||^{\frac{2}{m-1}}}}}
\]

将上式求出来的结果带入\(u_{ij}\)中，可得

\[u_{ij}=\frac{1}{\sum_{k=1}^{L}{\frac{1}{||x_j - C_k||^{\frac{2}{m-1}}}}}{\frac{1}{||x_j - C_i||^{\frac{2}{m-1}}}}\\
u_{ij}=\frac{1}{\sum_{k=1}^{L}{(\frac{||x_j - C_i||}{||x_j - C_k||})^{\frac{2}{m-1}}}}
\]

\(J\)对\(c_{i}\)求偏导：

\[\frac{\partial{J}}{\partial{C_i}}=\sum_{j=1}^{N}{u_{ij}^{m}2(x_j-C_i)(-1)}=0\\
\sum_{j=1}^{N}{u_{ij}^{m}(x_j-C_i)}=0\\
\sum_{j=1}^{N}{u_{ij}^{m}}x_j - C_i\sum_{s=1}^{N}{u_{is}^{m}}=0\\
C_i=\frac{\sum_{j=1}^{N}{u_{ij}^{m}}x_j}{\sum_{s=1}^{N}{u_{is}^{m}}}\\
C_i=\sum_{j=1}^{N}{\frac{u_{ij}^{m}}{\sum_{s=1}^{N}{u_{is}^{m}}}x_j}
\]

四、Matlab实现

%% ------------------------ 编码信息 -------------------------
%  Author: Lee Wen-Tsao
%  Time: 2021-09-01
%  Content: Fuzzy C-Means
%  Parameter:
%       n: 数据长度
%       k: 分类数目
%       m: 模糊指数，取值范围(1.5, 2.5)

%% ----------------------- 清理运行环境 -----------------------
clc;
clear;
close all;

%% 输入数据
Iris = uiimport('iris.data');
Iris = cellfun(@(x) regexp(x,',','split'), Iris.iris,'UniformOutput',false);
data = cellfun(@(x) x(:,1:4),Iris,'UniformOutput',false);
data = str2double(reshape([data{:}],4,150)');

%% 定义参数
[n, d] = size(data);
maxIter = 1000;
k = 3;
m = 2;
display = true;
epsilon = 0.01;

%% 初始化隶属度矩阵
random_mat = rand(k,n);
sum_mat = sum(random_mat);
MembershipMat = random_mat ./ sum_mat;

%% 拟合数据
obj_fcn = zeros(1,maxIter);
for it=1:maxIter
    % 更新簇心
    centers = updateCenter(MembershipMat, data, m, k);
    % 更新隶属矩阵
    [MembershipMat, dists] = updateMembershipMat(centers, data, k, n, m);
    % 计算目标函数值
    obj_fcn(it) = sum(sum((MembershipMat.^m).*(dists.^2)));
    if display
        fprintf('Iteration count=%d, obj_fcn=%f\n',it, obj_fcn(it))
    end
    if it > 1
        if abs(obj_fcn(it)-obj_fcn(it-1))<epsilon, break;end
    end
end
tatgets = getLabel(MembershipMat);

%% 根据隶属度矩阵更新聚类中心
function Centroids = updateCenter(MembershipMat, data, m, k)
    fm = MembershipMat.^m;
    summation = sum(fm, 2).*ones(k, size(data,2));
    Centroids = (fm*data)./summation;
end

%% 更新隶属度矩阵
function [Membership, dist] = updateMembershipMat(Centroids, data, k, n, m)
    dist = ones(k, n);
    for i=1:k
        dist(i,:) = vecnorm(data - Centroids(i,:), 2, 2)';
    end
    Mebership = dist.^(-2/(m-1));
    summation = sum(Mebership);
    Membership = (Mebership./summation);
end

%% 获取标签
function labels = getLabel(MembershipMat)
    [~, labels] = max(MembershipMat);
end

注意：鸢尾花(Iris)数据集来自UCI数据库。