第五章——支持向量机（Support Vector Machines）

svm可用于线性或非线性分类、回归、甚至异常检测。

svm尤其适用于中小数据集的复杂分类问题。

5.1 Linear SVM Classification

svm对feature scales敏感，如下图所示，左图中纵坐标范围远大于横坐标范围，决策边界会因为偏向于横坐标。右图进行了feature scaling之后，决策边界就好得多。

5.2 软间隔分类（Soft Margin Classification）

Scikit-Learn的SVM类有一个C超参数，C越小导致越宽的间隔但是更多的误分点。如下图所示，右侧C较小。C越小的模型也越容易一般化。如果SVM过拟合，可以尝试减小C进行调整。

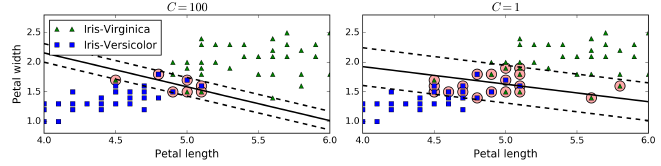
Scikit-Learn提供了LinearSVC类和SVC类，但是后者会慢得多，由于对于大的训练集，因此不推荐。此外还可以使用SGDClassifier(loss="hinge",alpha=1/(m*C))，这会使用SGD算法训练一个线性SVM分类器，这没有LinearSVC收敛得快，但可以处理海量数据集或者在线分类任务。

The LinearSVC class regularizes the bias term（这半句没看懂）, so you should center the training set first by subtracting its mean.这在调用StandardScaler时会自动完成。同时要设置损失超参数为"hinge"，对偶（dual）超参数为False（除非特征数多于样本）。

5.3 Nonlinear SVM Classification

有些数据集本身就不是线性的，一个解决方案就是增加特征，比如多项式特征，然后使用线性SVM进行训练。这与4.3的多项式回归类似。

5.3.1 多项式核（Polynomial Kernel）

增加多项式特征很简单，但是次数太低无法拟合复杂函数，次数太高又会增加大量的特征。

幸运的是，SVMs可以使用一种被称作核技巧（kernel trick）的数学方法。它和增加很多多项式特征的表现一样，但实际上有没有增加特征。

5.3.2 增加相似度特征（Adding Similarity Features）

另一个处理非线性问题的方式是使用相似度函数增加特征，该函数计算所有样本点与给定样本点的相似度。比如，我看可以定义$\gamma = 0.3$的高斯径向基函数（Radial Basis Function，RBF）为相似度函数。

Gaussian RBF：

$\phi \gamma(X,l) = exp(-\gamma\left \| X - l \right \|^2)$

至于怎么选取给定的样本点，一个简单的方法是训练集中的所有样本都作为给定样本点，以便新的数据集尽可能的线性可分。但是这样的话，如果训练集很大，那就会增加太多的的特征。

5.3.3 Gaussian RBF Kernel

与多项式核代替直接增加多项式特征相似，我们也可以使用高斯RBF核代替直接增加相似度特征。

还有一些其它的很少用到的核函数。比如一些核函数是专门处理特殊数据结构的。String kernels可用于文本或DNA序列分类（比如string subsequence kernel或者基于Levenshtein distance的核）。

如何选择核函数呢？一般来说，首先应该尝试线性分类器，尤其是训练集很大或者特征很多。如果训练集不是特别大，也可以尝试Gaussian RBF kernel，图适用于大多数情况。

5.3.4 计算复杂度（Computational Complexity）

LinearSVC基于liblinear，它实现了线性SVMs的优化算法，但是不支持核技巧，计算复杂度大概$O(m \times n)$。

SVC基于libsvm，它实现了一个支持核技巧的算法，计算复杂度在$O(m^2 \times n)$到$O(m^3 \times n)$之间。

5.4 SVM回归

与分类问题求得类别间的最大间隔不同，SVM回归的目的是使得间隔里面包含最多的样本点。间隔的宽度通过超参数$\varepsilon$控制，如下图所示：

5.5 底层知识（Under the Hood）

svm的一些理论知识可参考支持向量机。

5.5.6 在线SVMs

这个有时间再了解吧。