617. 合并二叉树 Golang实现

题目描述：

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。



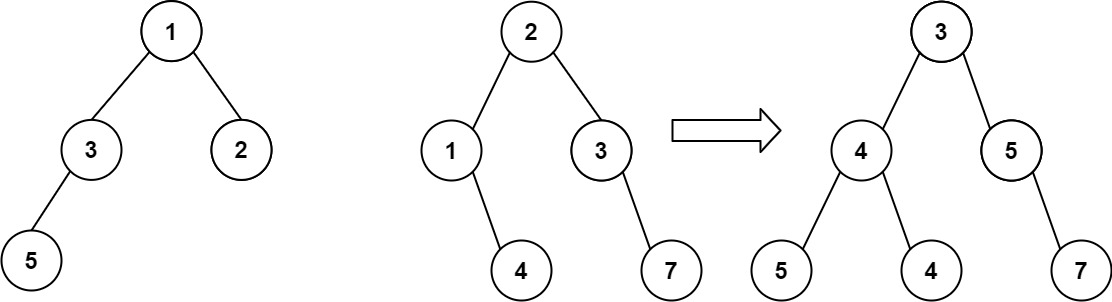
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]

输出：[3,4,5,5,4,null,7]

思路分析：

这个题目是第一次遇到的同时处理两个二叉树的问题。但是和单颗二叉树处理方法类似的关键在于：合并两个二叉树，如果树的结果一致，直接合并，不一致的时候，比如root1没有左子树，root2有。则直接root1.Right = root2.Right即可。

下面是一个自顶向下的递归实现，当遍历到某个树的叶子节点就return。

点击查看代码

func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
   if root1==nil{
       return root2
   }
   if root2 == nil {
       return root1
   }
   root1.Val+=root2.Val
   root1.Left = mergeTrees(root1.Left,root2.Left)
   root1.Right = mergeTrees(root1.Right,root2.Right)
   return root1
}

迭代做法

用层序遍历来解决这个问题，当两棵树的每层都是满的时候才进行层序入队，某则就是某颗有空树，就直接进行拼接，不能进行入队操作。

点击查看代码

func mergeTrees(t1 *TreeNode, t2 *TreeNode) *TreeNode {
    // 如果 t1 为空，直接返回 t2
    if t1 == nil {
        return t2
    }
    // 如果 t2 为空，直接返回 t1
    if t2 == nil {
        return t1
    }

    // 初始化队列
    que := []*TreeNode{t1, t2}
    // 使用队列进行层次遍历
    for len(que) > 0 {
        // 从队列中弹出两个节点
        node1 := que[0]
        que = que[1:]
        node2 := que[0]
        que = que[1:]

        // 合并两个节点的值
        node1.Val += node2.Val

        // 如果两个树的左节点都不为空，加入队列
        if node1.Left != nil && node2.Left != nil {
            que = append(que, node1.Left, node2.Left)
        }
        // 如果 t1 的左节点为空而 t2 的左节点不为空，就赋值过去
        if node1.Left == nil && node2.Left != nil {
            node1.Left = node2.Left
        }

        // 如果两个树的右节点都不为空，加入队列
        if node1.Right != nil && node2.Right != nil {
            que = append(que, node1.Right, node2.Right)
        }
        // 如果 t1 的右节点为空而 t2 的右节点不为空，就赋值过去
        if node1.Right == nil && node2.Right != nil {
            node1.Right = node2.Right
        }
    }
    return t1
}