洛谷P2701 [USACO5.3] 巨大的牛棚Big Barn 题解

怎么题解全是清一色的 dp？可以用笛卡尔树啊（虽然麻烦了很多，但是我热爱）！

题目传送门。

笛卡尔树的介绍

笛卡尔树，是一种二叉搜索树，它满足如下条件：

• 每个节点的编号满足二叉搜索树的性质。
• 每个节点的权值满足小根堆或大根堆的性质。

大概是这个样子：

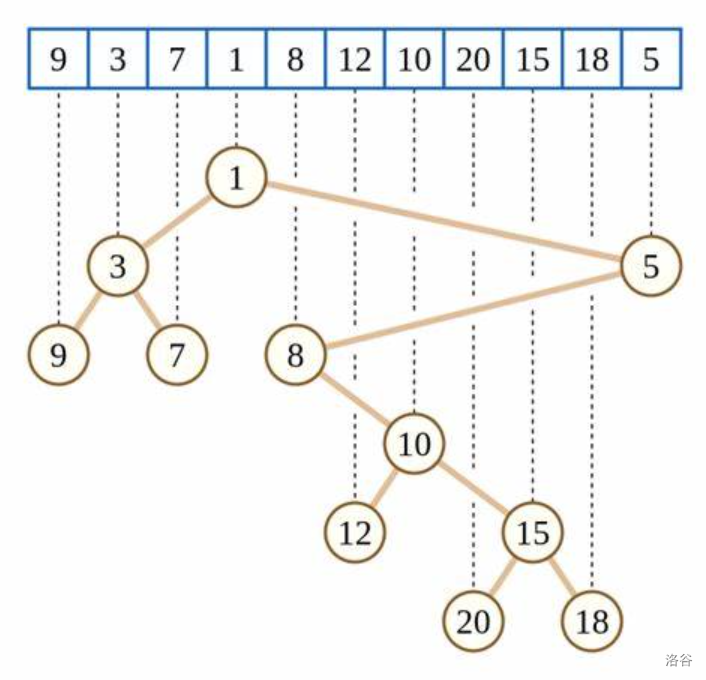
笛卡尔树的建树

请看这里。

笛卡尔树的用途

它可以用来解决区间最值问题，它有一个重要性质：当这个笛卡尔树为小根堆时，\(\min_{i = l}^r a_i = a_{\operatorname{lca}(l,r)}\)，当这个笛卡尔树为大根堆时，\(\max_{i = l}^r a_i = a_{\operatorname{lca}(l,r)}\)。

所以，我们要求一个区间的最小值，只需将笛卡尔树建成小根堆的样式，按照性质求，如果要求一个区间的最大值，只需将笛卡尔树建成大根堆的样式，按照性质求。

当然，它还可以求有多少个区间的最小值或最大值为 \(a_i\)，只需看有对少对区间的两端点的最近公共祖先是 \(i\) 即可，由于要使 \(\operatorname{lca}(l,r) = i\)，那么 \(l\) 肯定在 \(i\) 的左子树或是 \(i\)，\(r\) 肯定在 \(i\) 的右子树或是 \(i\)，所以，设 \(s_i\) 表示 \(i\) 这个子树的大小，\(l_i\) 表示 \(i\) 的左儿子，\(r_i\) 表示 \(i\) 的右儿子，则就有 \((s_{l_i}+1) \times (s_{r_i}+1)\) 对区间的两端点的最近公共祖先为 \(i\)。

此题做法

设当前位置有树则当前位置为 \(1\)，当前位置没有树则当前位置为 \(0\)。

首先使用前缀和将每个位置往上有多少个连续的 \(1\)，设这个数组为 \(f\)。

我们枚举每一行的每个位置。

然后放个假设图（其中一行）：

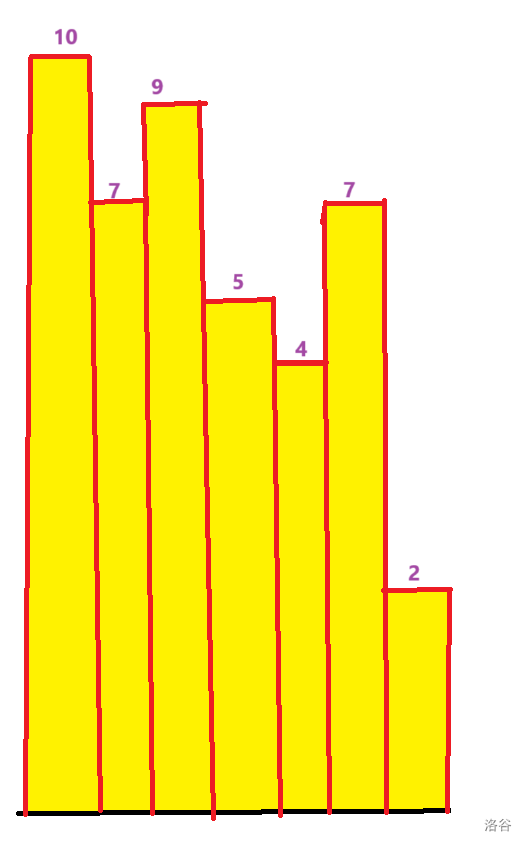
图可能有点丑，请谅解（感谢）！！

假设这是第 \(k\) 行的 \(f\) 数组情况，其中第 \(i\) 个柱子的高度是 \(f_{k,i}\) 对于这第 \(k\) 行，如果要使矩阵的高为第二个柱子，那么它必须得找高度比它高或相等的柱子拼起来才行，所以得找到最左边的一个柱子 \(j\)，使得 \(j \le i\) 并且从 \(j\) 到 \(i\) 这些柱子的高度都大于等于等于柱子 \(i\) 的高度，那么这个 \(j\) 就是高为第 \(i\) 个柱子的矩形的左端点，然后再找到 \(k\)，使得 \(k<i\) 并且从 \(i\) 到 \(k\) 这些柱子的高度都大于等于等于柱子 \(i\) 的高度，那么这个 \(k\) 就是高为第 \(i\) 个柱子的矩形的右端点，到这里大家都知道可以用单调栈做了吧，但是，我们是要用笛卡尔树的，所以还没完。实际上我们就是要找到区间长度最大的 \([j,k]\)，使得 \(\min_{q = j}^k a_q = a_i\)，那么就变成了上面说的笛卡尔树的用途的变形，由于我们要使 \([j,k]\) 的长度最大并且满足要求，那么 \(j\) 一定是 \(i\) 的左子树中编号最小的数（如果 \(i\) 没有左子树，那 \(j = i\)），\(k\) 一定是 \(i\) 的右子树中编号最大的数（如果 \(i\) 没有右子树，那 \(k = i\)），这样才能使 \([j,k]\) 长度最大且满足条件，知道了 \([j,k]\) 的长度之后，直接拿长度和当前柱子高度取个最小值就行了。然后求一个子树中编号最小的数和编号最大的数只需找到笛卡尔树的根，然后搜索一下，递推即可。

讲的这么详细，放个代码没问题吧：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+5;
int a[N][N];
int q[N];
int f[N][N];
int l[N];
int r[N];
int depmax[N];
int depmin[N];
int num[N];
void dfs(int x)
{
	depmax[x] = x;
	depmin[x] = x;
	if(l[x])
	{
		dfs(l[x]);
		depmin[x] = min(depmin[x],depmin[l[x]]);
		depmax[x] = max(depmax[x],depmax[l[x]]);
	}
	if(r[x])
	{
		dfs(r[x]);
		depmin[x] = min(depmin[x],depmin[r[x]]);
		depmax[x] = max(depmax[x],depmax[r[x]]);
	}
}
int main()
{
	int n,_;
	scanf("%d %d",&n,&_);
	while(_--)
	{
		int x,y;
		scanf("%d %d",&x,&y);
		a[x][y] = 1;
	}
	for(int i = 1;i<=n;i++)
	{
		for(int j = 1;j<=n;j++)
		{
			if(!a[i-1][j]&&!a[i][j])
			{
				f[i][j] = f[i-1][j]+!a[i][j];
			}
			else if(!a[i][j])
			{
				f[i][j] = 1;
			}
		}
	}
	int maxx = 0;
	for(int i = 1;i<=n;i++)
	{
		memset(l,0,sizeof(l));
		memset(r,0,sizeof(r));
		int t = 0;
		for(int j = 1;j<=n;j++)
		{
			while(t&&f[i][q[t]]>f[i][j])
			{
				l[j] = q[t];
				t--;
			}
			if(t)
			{
				r[q[t]] = j;
			}
			q[++t] = j;
		}
		for(int j = 1;j<=n;j++)
		{
			num[l[j]] = i;
			num[r[j]] = i;
		}
		for(int j = 1;j<=n;j++)
		{
			if(num[j]!=i)
			{
				dfs(j);
				break;
			}
		}
		for(int j = 1;j<=n;j++)
		{
			int ll,rr;
			if(l[j])
			{
				ll = min(depmin[l[j]],j);
			}
			else
			{
				ll = j;
			}
			if(r[j])
			{
				rr = max(depmax[r[j]],j);
			}
			else
			{
				rr = j;
			}
			maxx = max(maxx,min(f[i][j],rr-ll+1));
		}
	}
	printf("%d",maxx);
	return 0;
}