js算法：分治法-棋盘覆盖
在一个 2^k * 2^k 个方格组成的棋盘中，若恰有一个方格与其他方格不同。则称该方格为一特殊方格，称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对不论什么 k>=0 。有 4^k 种不同的特殊棋盘。
下图所看到的的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。
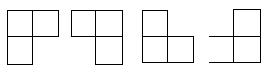
在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的全部方格，且不论什么 2 个 L 型骨牌不得重叠覆盖。
易知，在不论什么一个 2^k * 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。
用分治策略，能够设计解棋盘问题的一个简捷的算法。
当 k>0 时，将 2^k * 2^k 棋盘切割为 4 个 2^(k-1) * 2^(k-1) 子棋盘，例如以下图所看到的。
特殊方格必位于 4 个较小子棋盘之中的一个中，其余 3 个子棋盘中无特殊方格。
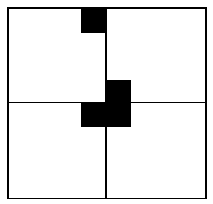
为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘，我们能够用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处。例如以下图所看到的。这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用 这样的切割。直至棋盘简化为 1x1 棋盘。
附代码：
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN">
<HTML>
<HEAD>
<TITLE> New Document </TITLE>
<META NAME="Generator" CONTENT="EditPlus">
<META NAME="Author" CONTENT="">
<META NAME="Keywords" CONTENT="">
<META NAME="Description" CONTENT="">
<script type="text/javascript" src="jquery-1.7.2.min.js"></script>
<script type="text/javascript" src="json2.js"></script>
<style>
table,td{
border:1px solid gray;
text-align:center;
color:white;
}
</style>
<script>
var t=0;
var color_arr=['red','yellow','green','blue','purple','orange','pink'];
var num
function initTable(){
$("#container").html('');
var table=$("<table></table>");
num=Math.pow(2,parseInt($("#txt_k").val()));
var width=document.body.clientWidth*0.4/num;
for(var i=0;i<num;i++){
var tr=$("<tr style='width:"+width*num+"px;height:"+width+"px;'></tr>");
for(var j=0;j<num;j++){
var td=$("<td style='width:"+width+"px;height:"+width+"px;'> </td>");
if(i==parseInt($("#txt_x").val())-1&&j==parseInt($("#txt_y").val())-1)
td.css("background-color","black");
tr.append(td);
}
table.append(tr);
}
$("#container").append(table);
} function calcTable(){
var dr=parseInt($("#txt_x").val())-1;
var dc=parseInt($("#txt_y").val())-1;
t=0;
chessBoard(0,0,dr,dc,num);
} //tr tc子棋盘左上角坐标 dr dc特殊格子坐标 size子棋盘格子数
function chessBoard(tr,tc,dr,dc,size){
var s,t1;
if(size==1)
return;
t1=++t;
s=size/2;
var color=color_arr[t1%color_arr.length];
//-------------左上角子棋盘-----------------
if(dr<tr+s&&dc<tc+s){
//特殊格子在右上角,递归处理子棋盘
chessBoard(tr,tc,dr,dc,s);
}else{
//处理右下角环绕切割点的棋盘
//标记特殊棋盘
$("table tr").eq(tr+s-1).find("td").eq(tc+s-1).text(t1);
$("table tr").eq(tr+s-1).find("td").eq(tc+s-1).css("background-color",color);
chessBoard(tr,tc,tr+s-1,tc+s-1,s);
} //--------------右上角棋盘-------------------
if(dr>=tr+s&&dc<tc+s){
chessBoard(tr+s,tc,dr,dc,s);
}else{
//左下角格子
$("table tr").eq(tr+s).find("td").eq(tc+s-1).text(t1);
$("table tr").eq(tr+s).find("td").eq(tc+s-1).css("background-color",color);
chessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
//--------------左下角棋盘-------------------
if(dr<tr+s&&dc>=tc+s){
chessBoard(tr,tc+s,dr,dc,s);
}else{
$("table tr").eq(tr+s-1).find("td").eq(tc+s).text(t1);
$("table tr").eq(tr+s-1).find("td").eq(tc+s).css("background-color",color);
chessBoard(tr,tc+s,tr+s-1,tc+s,s);
}
//--------------右下角棋盘-------------------
if(dr>=tr+s&&dc>=tc+s){
chessBoard(tr+s,tc+s,dr,dc,s);
}else{
//setTimeout("setColor("+tr+s+","+tc+s+",'"+color+"')",1000);
$("table tr").eq(tr+s).find("td").eq(tc+s).text(t1);
$("table tr").eq(tr+s).find("td").eq(tc+s).css("background-color",color);
chessBoard(tr+s,tc+s,tr+s,tc+s,s);
} } </script>
</HEAD>
<BODY style="text-align:center">
<div>
级数:
<input type="text" id="txt_k"/>
坐标X：
<input type="text" id="txt_x"/>
坐标Y:
<input type="text" id="txt_y"/>
<input type="button" id="btn" value="初始化表格" onclick="initTable()"/>
<input type="button" id="btn" value="開始棋盘覆盖" onclick="calcTable()"/>
</div>
<div id='container' style="margin:0 auto;">
</div>
</BODY>
</HTML>
js算法：分治法-棋盘覆盖的更多相关文章
- Java算法——分治法
一.基本概念 在计算机科学中,分治法是一种很重要的算法.字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简 ...
- [C++] 分治法之棋盘覆盖、循环赛日程表
一.分治的基本思想 将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之. 对于一个规模为 n 的问题,若问题可以容易地解决,则直接解决,否则将其分解为 k 个规模较小的子 ...
- js算法：分治法-循环赛事日程表
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/ ...
- Leedcode算法专题训练（分治法）
归并排序就是一个用分治法的经典例子,这里我用它来举例描述一下上面的步骤: 1.归并排序首先把原问题拆分成2个规模更小的子问题. 2.递归地求解子问题,当子问题规模足够小时,可以一下子解决它.在这个例子 ...
- 算法与数据结构基础 - 分治法(Divide and Conquer)
分治法基础 分治法(Divide and Conquer)顾名思义,思想核心是将问题拆分为子问题,对子问题求解.最终合并结果,分治法用伪代码表示如下: function f(input x size ...
- 《github一天一道算法题》：分治法求数组最大连续子序列和
看书.思考.写代码. /*************************************** * copyright@hustyangju * blog: http://blog.csdn. ...
- 算法笔记_065:分治法求逆序对（Java）
目录 1 问题描述 2 解决方案 2.1 蛮力法 2.2 分治法(归并排序) 1 问题描述 给定一个随机数数组,求取这个数组中的逆序对总个数.要求时间效率尽可能高. 那么,何为逆序对? 引用自百度 ...
- 分治法 - Divide and Conquer
在计算机科学中,分治法是一种很重要的算法.分治法即『分而治之』,把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的 ...
- bzoj 2706: [SDOI2012]棋盘覆盖 Dancing Link
2706: [SDOI2012]棋盘覆盖 Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 255 Solved: 77[Submit][Status] ...
随机推荐
- 利用js在文本框末尾获得焦点
function moveEnd(obj) { obj.focus(); var len = obj.value.length; if (document.selection) { var sel = ...
- HDU 1269 -- 迷宫城堡【有向图求SCC的数目 && 模板】
迷宫城堡 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submi ...
- COGS 2580. [HZOI 2015]偏序 II
COGS 2580. [HZOI 2015]偏序 II 题目传送门 题目大意:给n个元素,每个元素有具有4个属性a,b,c,d,求i<j并且ai<aj,bi<bj,ci<cj, ...
- 使用CNN做电影评论的负面检测——本质上感觉和ngram或者LSTM同，因为CNN里图像检测卷积一般是3x3，而文本分类的话是直接是一维的3、4、5
代码如下: from __future__ import division, print_function, absolute_import import tensorflow as tf impor ...
- DB-MySQL：MySQL NULL 值处理
ylbtech-DB-MySQL:MySQL NULL 值处理 1.返回顶部 1. MySQL NULL 值处理 我们已经知道 MySQL 使用 SQL SELECT 命令及 WHERE 子句来读取数 ...
- 37.Qt网络与通信
1 获取本机网络与通信 在网络应用中,经常需要获得本机的主机名.IP地址和硬件地址等网络信息.运用QHostInfo,QNetWorkInterface,QNetworkAddressEntry可获得 ...
- 匹配替换指定文本为html标签
最近看了一道前端面试题,是关于正则的,用尽可能低复杂度的函数,匹配替换指定文本为html标签,题目是这样的: 特定语法匹配替换 说明:匹配字符串中形如 =g文字文字= 的语法,并将相应部分转化为对应的 ...
- BZOJ 4129 树上带修莫队+线段树
思路: 可以先做做BZOJ3585 是序列上的mex 考虑莫队的转移 如果当前数字出现过 线段树上把它置成1 对于询问 二分ans 线段树上查 0到ans的和 是不是ans+1 本题就是把它搞到了序列 ...
- EntityFramework使用及优化
1. 简介 ORM框架:Object Relation Mapping,用操作对象的方式来操作数据库 其它框架:Dapper.NHibernate,首推EF,微软官方的. EF底层还是ADO.NET实 ...
- vue强制绑定css3的缩放效果transfrom:scale()
vue不提供 transfrom:scale(1.5) : 会报错 ,错误是 "TypeError: _vm.scale is not a function": 原因:Vue将其 ...