【LeetCode】105#从前序与中序遍历序列构造二叉树

题目描述

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:

你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

---

解题思路

首先列举一下二叉树的三种常见遍历方式：

• 前序遍历：根 - 左 - 右
• 中序遍历：左 - 根 - 右
• 后序遍历：左 - 右 - 根

可以发现，「前中后」是指根节点在三个节点中的相对顺序。

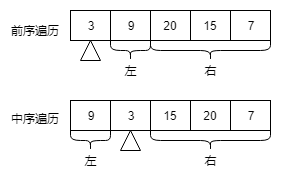
根据二叉树遍历的特点，前序遍历的第一个节点一定是整棵二叉树的根节点，根据这一特点找到根节点，新建一棵二叉树。找到根节点后，在中序遍历的序列中找到根节点的值对应的位置，以这个节点为界，左边是根节点的左子树，右边是根节点的右子树。最后利用递归的方法，构造起整棵二叉树。

具体实现

我们需要一个辅助函数

private TreeNode help(int startPre, int startIn,int endIn,int[] preorder, int[] inorder)

其中：

• int satrtPre用来在前序遍历序列中定位根节点
• int startIn用来在中序遍历序列中定位左子树的起点（终点取决于根节点在中序遍历序列中的位置）
• int endIn用来在中序遍历序列中定位右子树的终点（起点取决于根节点在中序遍历序列中的位置）

此外，在每次迭代中，都要更新当前根节点在对应的中序遍历序列中的索引，用int curInIndex表示

源代码

public TreeNode buildTree (int[] preorder, int[] inorder) {
    return help(0,0,inorder.length - 1,preorder,inorder);
}

private TreeNode help(int startPre, int startIn,int endIn,int[] preorder, int[] inorder) {
    if (startPre > preorder.length - 1 || startIn > endIn) {
        return null;
    }

    TreeNode root = new TreeNode(preorder[startPre]);
    int curInIndex = 0; // 前根节点在对应的中序遍历序列中的索引
    for (int i = startIn; i <= endIn; i++) {
        if (root.val == inorder[i]) {
            curInIndex = i;
        }
    }
    root.left = help(startPre + 1,startIn,curInIndex - 1,preorder,inorder);
    root.right = help(startPre + curInIndex - startIn + 1, curInIndex + 1, endIn, preorder, inorder);
    return root;
}

心得体会

在二叉树的相关题目中，递归是很常用的一个方法，关键是找到递归的最小情况。现在掌握的还不熟练，需要多做一些树和链表相关的题目。