线性判别分析(Linear Discriminant Analysis, LDA）算法初识

LDA算法入门

一． LDA算法概述：

线性判别式分析(Linear Discriminant Analysis, LDA)，也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD)，是模式识别的经典算法，它是在1996年由Belhumeur引入模式识别和人工智能领域的。性鉴别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。因此，它是一种有效的特征抽取方法。使用这种方法能够使投影后模式样本的类间散布矩阵最大，并且同时类内散布矩阵最小。就是说，它能够保证投影后模式样本在新的空间中有最小的类内距离和最大的类间距离，即模式在该空间中有最佳的可分离性。

二． LDA假设以及符号说明：

假设对于一个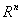空间有m个样本分别为x1,x2,……xm 即 每个x是一个n行的矩阵，其中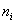表示属于i类的样本个数，假设有一个有c个类，则。

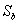………………………………………………………………………… 类间离散度矩阵

………………………………………………………………………… 类内离散度矩阵

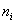………………………………………………………………………… 属于i类的样本个数

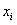 …………………………………………………………………………… 第i个样本

 …………………………………………………………………………… 所有样本的均值

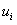 …………………………………………………………………………… 类i的样本均值

三． 公式推导，算法形式化描述

根据符号说明可得类i的样本均值为：

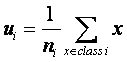 …………………………………………………………………… （1）

同理我们也可以得到总体样本均值：

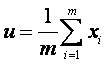………………………………………………………………………… （2）

根据类间离散度矩阵和类内离散度矩阵定义，可以得到如下式子：

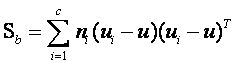  ……………………………………………… （3）

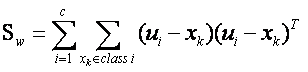…………………………………… （4）

当然还有另一种类间类内的离散度矩阵表达方式：

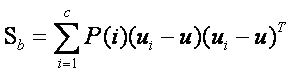
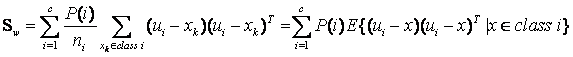其中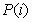是指i类样本的先验概率，即样本中属于i类的概率（），把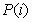代入第二组式子中，我们可以发现第一组式子只是比第二组式子都少乘了1/m，我们将在稍后进行讨论，其实对于乘不乘该1/m，对于算法本身并没有影响，现在我们分析一下算法的思想，

我们可以知道矩阵的实际意义是一个协方差矩阵，这个矩阵所刻画的是该类与样本总体之间的关系，其中该矩阵对角线上的函数所代表的是该类相对样本总体的方差（即分散度），而非对角线上的元素所代表是该类样本总体均值的协方差（即该类和总体样本的相关联度或称冗余度），所以根据公式（3）可知（3）式即把所有样本中各个样本根据自己所属的类计算出样本与总体的协方差矩阵的总和，这从宏观上描述了所有类和总体之间的离散冗余程度。同理可以的得出（4）式中为分类内各个样本和所属类之间的协方差矩阵之和，它所刻画的是从总体来看类内各个样本与类之间（这里所刻画的类特性是由是类内各个样本的平均值矩阵构成）离散度，其实从中可以看出不管是类内的样本期望矩阵还是总体样本期望矩阵，它们都只是充当一个媒介作用，不管是类内还是类间离散度矩阵都是从宏观上刻画出类与类之间的样本的离散度和类内样本和样本之间的离散度。

LDA做为一个分类的算法，我们当然希望它所分的类之间耦合度低，类内的聚合度高，即类内离散度矩阵的中的数值要小，而类间离散度矩阵中的数值要大，这样的分类的效果才好。

这里我们引入Fisher鉴别准则表达式：

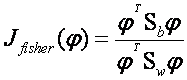…………………………………………………………… （5）

其中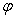为任一n维列矢量。Fisher线性鉴别分析就是选取使得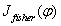达到最大值的矢量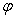作为投影方向，其物理意义就是投影后的样本具有最大的类间离散度和最小的类内离散度。

我们把公式（4）和公式（3）代入公式（5）得到：

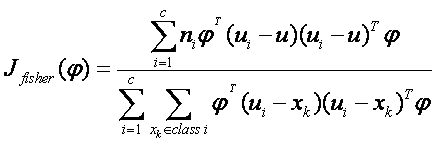
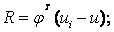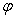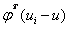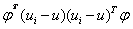我们可以设矩阵其中可以看成是一个空间，也就是说是构成的低维空间（超平面）的投影。也可表示为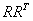，而当样本为列向量时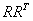，即表示在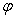空间的几何距离的平方。所以可以推出fisher线性鉴别分析表达式的分子即为样本在投影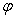空间下的类间几何距离的平方和，同理也可推出分母为样本在投影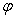空间下的类内几何距离的平方差，所以分类问题就转化到找一个低维空间使得样本投影到该空间下时，投影下来的类间距离平方和与类内距离平方和之比最大，即最佳分类效果。

所以根据上述思想，即通过最优化下面的准则函数找到有一组最优鉴别矢量构成的投影矩阵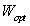（这里我们也可以看出1/m可以通过分子分母约掉，所以前面所提到的第一组公式和第二组公式所表达的效果是一样的）.

……………… （6）

可以证明，当为非奇异（一般在实现LDA算法时，都会对样本做一次PCA算法的降维，消除样本的冗余度，从而保证是非奇异阵，当然即使为奇异阵也是可以解的，可以把或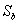对角化，这里不做讨论，假设都是非奇异的情况）时，最佳投影矩阵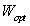的列向量恰为下来广义特征方程

………………………………………………………………………… （7）

的d个最大的特征值所对应的特征向量(矩阵的特征向量)，且最优投影轴的个数d<=c-1.

根据（7）式可以推出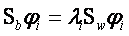……………………………………………… （8）

又由于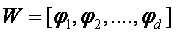

下面给出验证：把（7）式代入（6）式可得：

四． 算法的物理意义和思考

4.1 用一个例子阐述LDA算法在空间上的意义

下面我们利用LDA进行一个分类的问题：假设一个产品有两个参数来衡量它是否合格，

我们假设两个参数分别为：

参数A	参数B	是否合格
2.95	6.63	合格
2.53	7.79	合格
3.57	5.65	合格
3.16	5.47	合格
2.58	4.46	不合格
2.16	6.22	不合格
3.27	3.52	不合格

实验数据来源：http://people.revoledu.com/kardi/tutorial/LDA/Numerical%20Example.html

所以我们可以根据上图表格把样本分为两类，一类是合格的，一类是不合格的，所以我们可以创建两个数据集类：

cls1_data =

2.9500    6.6300

2.5300    7.7900

3.5700    5.6500

3.1600    5.4700

cls2_data =

2.5800    4.4600

2.1600    6.2200

3.2700    3.5200

其中cls1_data为合格样本，cls2_data为不合格的样本，我们根据公式（1），（2）可以算出合格的样本的期望值，不合格类样本的合格的值，以及总样本期望：

E_cls1 =

3.0525    6.3850

E_cls2 =

2.6700    4.7333

E_all =

2.8886    5.6771

我们可以做出现在各个样本点的位置：

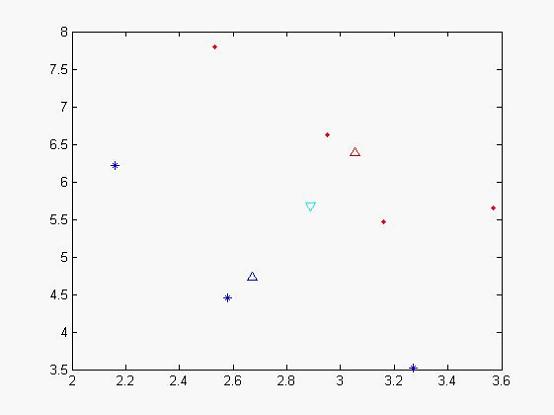
图一

其中蓝色‘*’的点代表不合格的样本，而红色实点代表合格的样本，天蓝色的倒三角是代表总期望，蓝色三角形代表不合格样本的期望，红色三角形代表合格样本的期望。从x，y轴的坐标方向上可以看出，合格和不合格样本区分度不佳。

我们在可以根据表达式（3），（4）可以计算出类间离散度矩阵和类内离散度矩阵：

Sb =

0.0358    0.1547

0.1547    0.6681

Sw =

0.5909   -1.3338

-1.3338    3.5596

我们可以根据公式（7），（8）算出特征值以及对应的特征向量：

L =

0.0000         0

0    2.8837

对角线上为特征值，第一个特征值太小被计算机约为0了

与他对应的特征向量为

V =

-0.9742   -0.9230

0.2256   -0.3848

根据取最大特征值对应的特征向量：（-0.9230,-0.3848)，该向量即为我们要求的子空间，我们可以把原来样本投影到该向量后 所得到新的空间（2维投影到1维，应该为一个数字）

new_cls1_data =

-5.2741

-5.3328

-5.4693

-5.0216

为合格样本投影后的样本值

new_cls2_data =

-4.0976

-4.3872

-4.3727

为不合格样本投影后的样本值，我们发现投影后，分类效果比较明显，类和类之间聚合度很高，我们再次作图以便更直观看分类效果

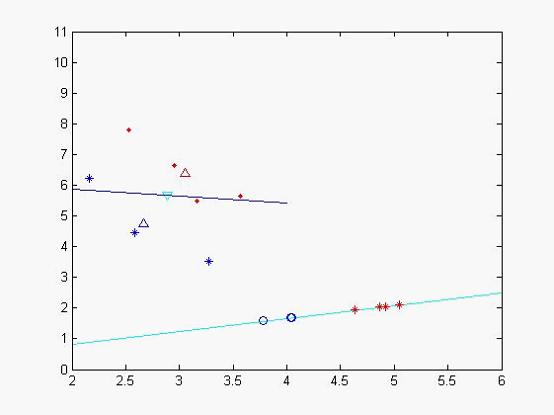
图二

蓝色的线为特征值较小所对应的特征向量，天蓝色的为特征值较大的特征向量，其中蓝色的圈点为不合格样本在该特征向量投影下来的位置，二红色的‘*’符号的合格样本投影后的数据集，从中个可以看出分类效果比较好（当然由于x，y轴单位的问题投影不那么直观）。

我们再利用所得到的特征向量，来对其他样本进行判断看看它所属的类型，我们取样本点

（2.81，5.46），

我们把它投影到特征向量后得到：result = -4.6947 所以它应该属于不合格样本。

4.2 LDA算法与PCA算法

在传统特征脸方法的基础上，研究者注意到特征值打的特征向量（即特征脸）并一定是分类性能最好的方向，而且对K-L变换而言，外在因素带来的图像的差异和人脸本身带来的差异是无法区分的，特征连在很大程度上反映了光照等的差异。研究表明，特征脸，特征脸方法随着光线，角度和人脸尺寸等因素的引入，识别率急剧下降，因此特征脸方法用于人脸识别还存在理论的缺陷。线性判别式分析提取的特征向量集，强调的是不同人脸的差异而不是人脸表情、照明条件等条件的变化，从而有助于提高识别效果。

线性判别式分析，又称为Fisher线性判别~（Linear discriminant analysis）(Fisher linear discriminant)

最大化类间均值，最小化类内方差

通过调整权重向量组件，可选择一个投影方向，最大化地类别分离性~

两个类的均值向量：

对样本进行投影时，使得类别最简单的分离，是投影的类别均值的分离~

最大化类间均值

   其中约束

最小化类内方差

，其中

Fisher 判别准则：

等价于：

其中：

对权重W求微分，使得J(W)最大化，当：

化简之~