POJ 1927 Area in Triangle

Area in Triangle

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 1674		Accepted: 821

Description

Given a triangle field and a rope of a certain length (Figure-1), you are required to use the rope to enclose a region within the field and make the region as large as possible. 

Input

The input has several sets of test data. Each set is one line containing four numbers separated by a space. The first three indicate the lengths of the edges of the triangle field, and the fourth is the length of the rope. Each of the four numbers have exactly four digits after the decimal point. The line containing four zeros ends the input and should not be processed. You can assume each of the edges are not longer than 100.0000 and the length of the rope is not longer than the perimeter of the field.

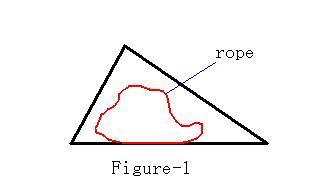
Output

Output one line for each case in the following format:

Case i: X

Where i is the case number, and X is the largest area which is rounded to two digits after the decimal point.

Sample Input

12.0000 23.0000 17.0000 40.0000
84.0000 35.0000 91.0000 210.0000
100.0000 100.0000 100.0000 181.3800
0 0 0 0

Sample Output

Case 1: 89.35
Case 2: 1470.00
Case 3: 2618.00

第三种情况:摘的别人的图

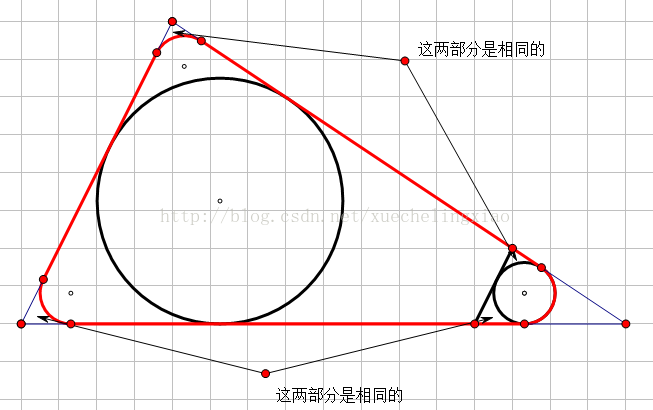
//数学一本通习题 2
//POJ 1927 求三角形内周长一定的图形的最大面积

//题意：给定一个三角形的三边长和一根绳子的长度，问将绳子放在三角形里能围起来的最大面积是多少

//余弦定理:
//cosA=b^2+c^2-a^2/2*bc
//cosB=a^2+c^2-b^2/2*ac
//cosC=a^2+b^2-c^2/2*ab

//三角形面积公式
//S=0.5*bc*sinA=0.5*bc*(1-cosA^2)
//三角形内接圆半径：
//r=2S/(a+b+c)

//如果绳子够长，长度>=三角形周长的话，那么能围成的最大面积就是三角形的面积
//如果绳子长度<=三角形内切圆周长的话，那么最大面积就是把绳子围成一个圆的面积（因为等周长的平面图形一定圆的面积最大，大概是初中学的）
//。如果介于两者中间呢？
//那就自己看blog去 
//求出相似比
//xsb=(C-d)/(C-2*PI*R)

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

const double PI=acos(-1.0);
const double eps=1e-;

double a,b,c,d;

int dcmp(double x)
{
    return x<-eps?-:x>eps;
}

int main()
{
    int cas=;
    while(scanf("%lf%lf%lf%lf",&a,&b,&c,&d))
    {
        if(!dcmp(a)&&!dcmp(b)&&!dcmp(c)&&!dcmp(d))
            break;
        ++cas;
        double C=a+b+c;
        double cosA=(b*b+c*c-a*a)/(*b*c);
        double S=0.5*b*c*sqrt(-cosA*cosA);
        double R=S*/C;
        if(d>=C)    //直接围三角形
            printf("Case %d: %.2lf\n",cas,S);
        else if(d<=*PI*R)        //绳子长度<=内切圆周长，围个圆
            printf("Case %d: %.2lf\n",cas,d*d/(*PI));
        else    //看blog去
        {
            double xsb=(C-d)/(C-*PI*R);    //相似比
            double r=R*xsb;
            printf("Case %d: %.2lf\n",cas,S-S*xsb*xsb+PI*r*r);
        }
    }
    return ;
}