用R做时间序列分析之ARIMA模型预测

昨天刚刚把导入数据弄好，今天迫不及待试试怎么做预测，网上找的帖子跟着弄的。

第一步.对原始数据进行分析

一.ARIMA预测时间序列

指数平滑法对于预测来说是非常有帮助的，而且它对时间序列上面连续的值之间相关性没有要求。但是，如果你想使用指数平滑法计算出预测区间，那么预测误差必须是不相关的， 而且必须是服从零均值、 方差不变的正态分布。即使指数平滑法对时间序列连续数值之间相关性没有要求，在某种情况下，我们可以通过考虑数据之间的相关性来创建更好的预测模型。自回归移动平均模型（ ARIMA） 包含一个确定（explicit）的统计模型用于处理时间序列的不规则部分，它也允许不规则部分可以自相关。

二.确定数据的差分

ARIMA 模型为平稳时间序列定义的。 因此， 如果你从一个非平稳的时间序列开始，首先你就需要做时间序列差分直到你得到一个平稳时间序列。如果你必须对时间序列做 d 阶差分才能得到一个平稳序列，那么你就使用ARIMA(p,d,q)模型，其中 d 是差分的阶数。

我们以每年女人裙子边缘的直径做成的时间序列数据为例。从 1866 年到 1911 年在平均值上是不平稳的。 随着时间增加， 数值变化很大。

下面是.dat数据：

下面进入预测。先导入数据：

> skirts <- scan("http://robjhyndman.com/tsdldata/roberts/skirts.dat",skip=5)      #导入在线数据，并跳过前5行

Read 46 items     #R控制台显示内容，表示共读取46行数据

> skirts<- ts(skirts,start = c(1866))   #设定时间1866开始

> plot.ts(skirts)       #画出图

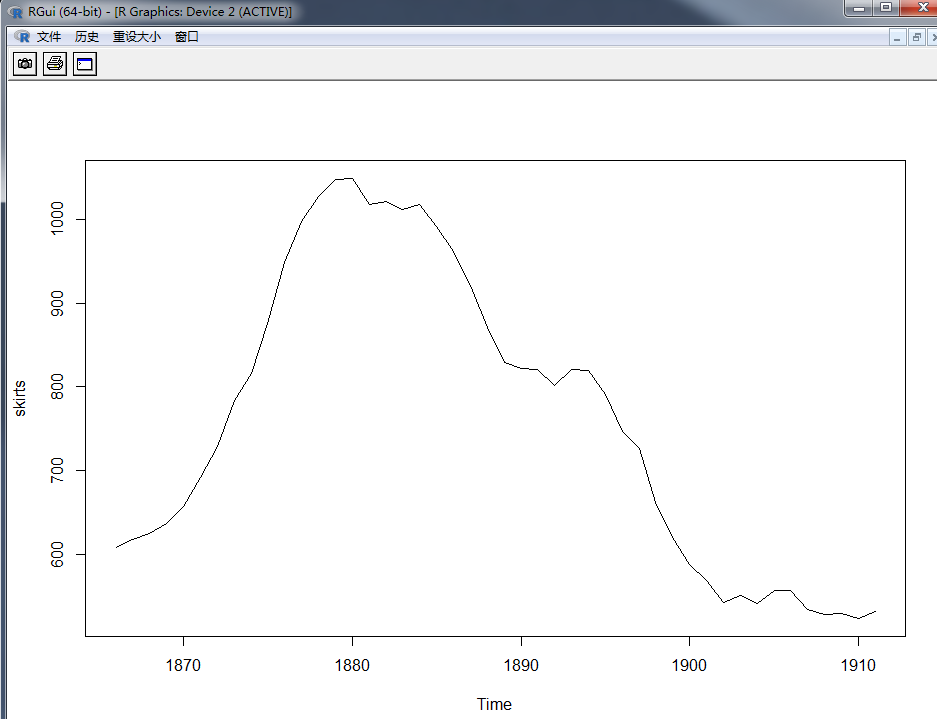
我们可以通过键入下面的代码来得到时间序列（数据存于“skirtsts”） 的一阶差分， 并画出差分序列的图:

> skirtsdiff<-diff(skirts,differences=1)  　　#一阶差分

> plot.ts(skirtsdiff) 　　 #画图

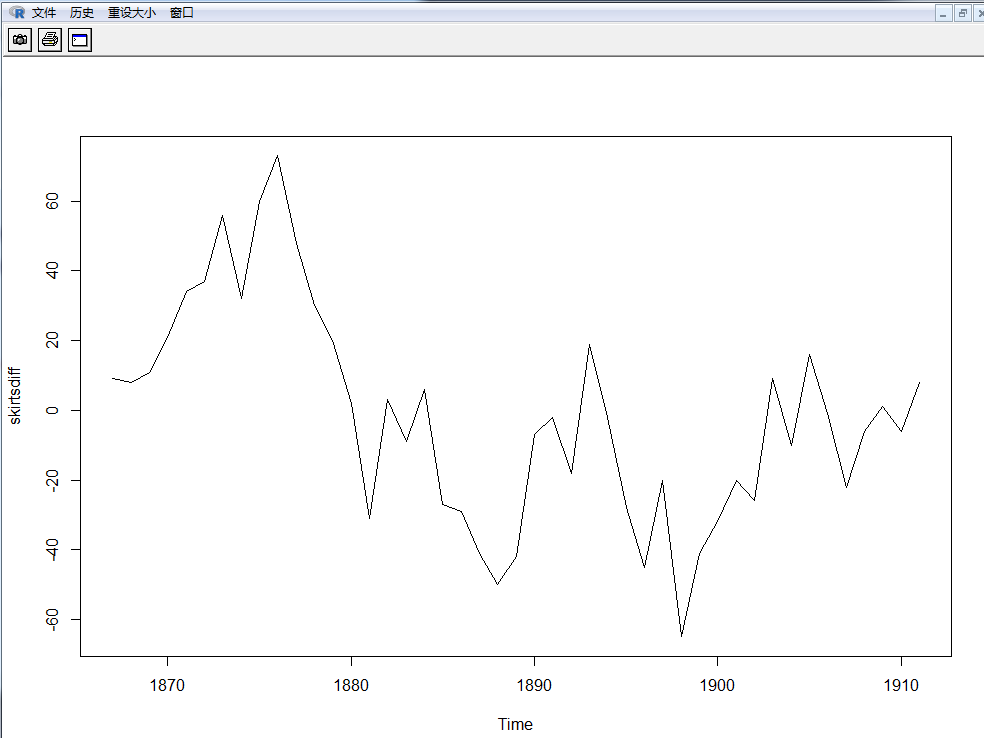
从一阶差分的图中可以看出，数据仍是不平稳的。我们继续差分。

> skirtsdiff2<-diff(skirts,differences=2)

> plot.ts(skirtsdiff2)

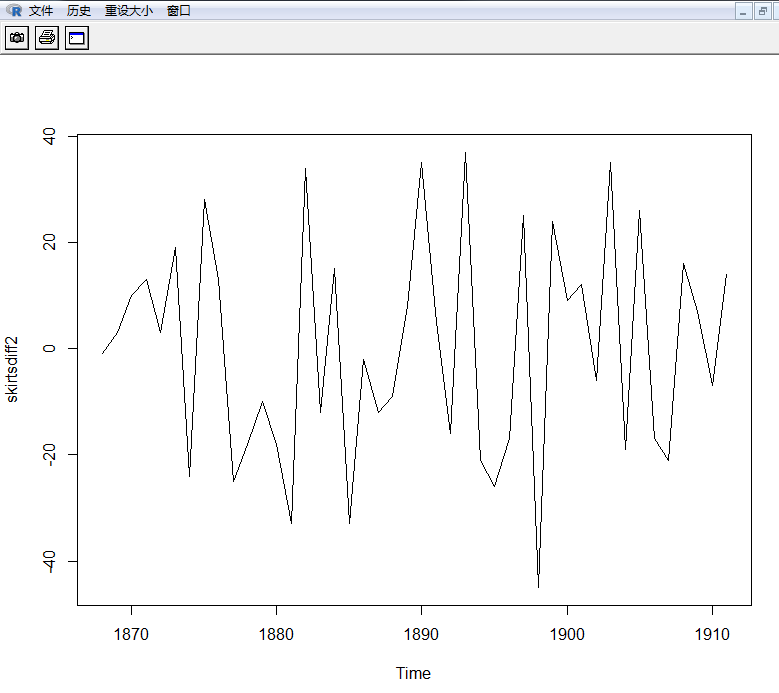
二次差分（上面）后的时间序列在均值和方差上确实看起来像是平稳的， 随着时间推移，时间序列的水平和方差大致保持不变。因此，看起来我们需要对裙子直径进行两次差分以得到平稳序列。

第二步，找到合适的ARIMA模型

如果你的时间序列是平稳的，或者你通过做 n 次差分转化为一个平稳时间序列， 接下来就是要选择合适的 ARIMA模型，这意味着需要寻找 ARIMA(p,d,q)中合适的 p 值和 q 值。为了得到这些，通常需要检查[平稳时间序列的（自）相关图和偏相关图。

我们使用 R 中的“acf()”和“pacf” 函数来分别（自） 相关图和偏相关图。“acf()”和“pacf 设定“plot=FALSE” 来得到自相关和偏相关的真实值。

> acf(skirtsdiff2,lag.max=20)

> acf(skirtsdiff2,lag.max=20,plot=FALSE)

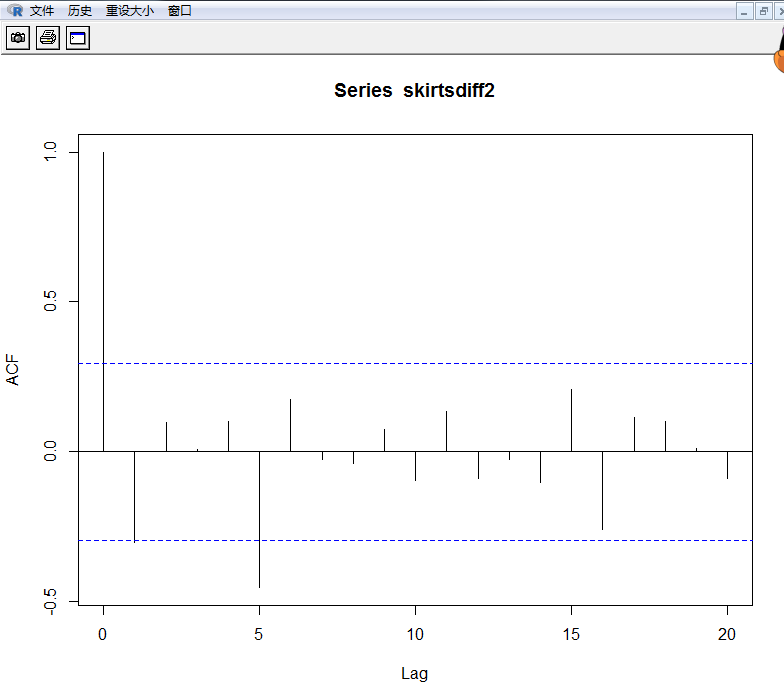
Autocorrelations of series ‘skirtsdiff2’, by lag

0 1 2 3 4 5 6 7 8 9 10 11 12
1.000 -0.303 0.096 0.009 0.102 -0.453 0.173 -0.025 -0.039 0.073 -0.094 0.133 -0.089
13 14 15 16 17 18 19 20
-0.027 -0.102 0.207 -0.260 0.114 0.101 0.011 -0.090

自相关图显示滞后1阶自相关值基本没有超过边界值，虽然5阶自相关值超出边界，那么很可能属于偶然出现的，而自相关值在其他上都没有超出显著边界，而且我们可以期望 1 到 20 之间的会偶尔超出 95%的置信边界。

> pacf(skirtsdiff2,lag.max=20)

> pacf(skirtsdiff2,lag.max=20,plot=FALSE)

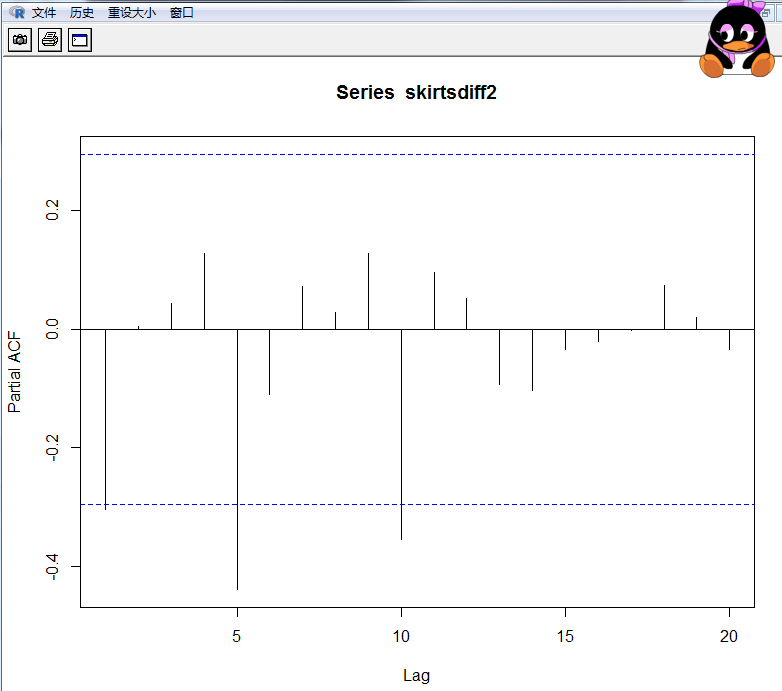
Partial autocorrelations of series ‘skirtsdiff2’, by lag

1 2 3 4 5 6 7 8 9 10 11 12 13
-0.303 0.005 0.043 0.128 -0.439 -0.110 0.073 0.028 0.128 -0.355 0.095 0.052 -0.094
14 15 16 17 18 19 20
-0.103 -0.034 -0.021 -0.002 0.074 0.020 -0.034

偏自相关值选5阶。

故我们的ARMIA模型为armia（1,2,5）

> skirtsarima<-arima(skirts,order=c(1,2,5))

> skirtsarima

Call:
arima(x = skirts, order = c(1, 2, 5))

SSeries: skirts

ARIMA(1,2,5)

Coefficients:
ar1 ma1 ma2 ma3 ma4 ma5
-0.4345 0.2762 0.1033 0.1472 0.0267 -0.8384
s.e. 0.1837 0.2171 0.2198 0.2716 0.1904 0.2888

sigma^2 estimated as 206.1: log likelihood = -183.8, aic = 381.6

所以，相应的评价标准的值：

sigma^2 estimated as 206.1:  log likelihood=-183.8

AIC=381.6   AICc=384.71   BIC=394.09

预测后5年裙子的边缘直径

>  skirtsarimaforecast<-forecast(skirtsarima,h=5,level=c(99.5))

>  skirtsarimaforecast

R控制台的输出为：

Point Forecast Lo 99.5 Hi 99.5

1912　　  548.5762  507.1167  590.0357
1913 　　 545.1793  459.3292  631.0295
1914 　　 540.9354  396.3768  685.4940
1915 　　 531.8838  316.2785  747.4892
1916 　　 529.1296  233.2625  824.9968

输入下面指令，得到残差图像：

> plot.forecast(skirtsarimaforecast$residuals)

第三步，检验

在指数平滑模型下， 观察 ARIMA 模型的预测误差是否是平均值为 0 且方差为常数的正态分布（服从零均值、方差不变的正态分布） 是个好主意，同时也要观察连续预测误差是否（自）相关。

> acf(skirtsarimaforecast$residuals,lag.max=20)

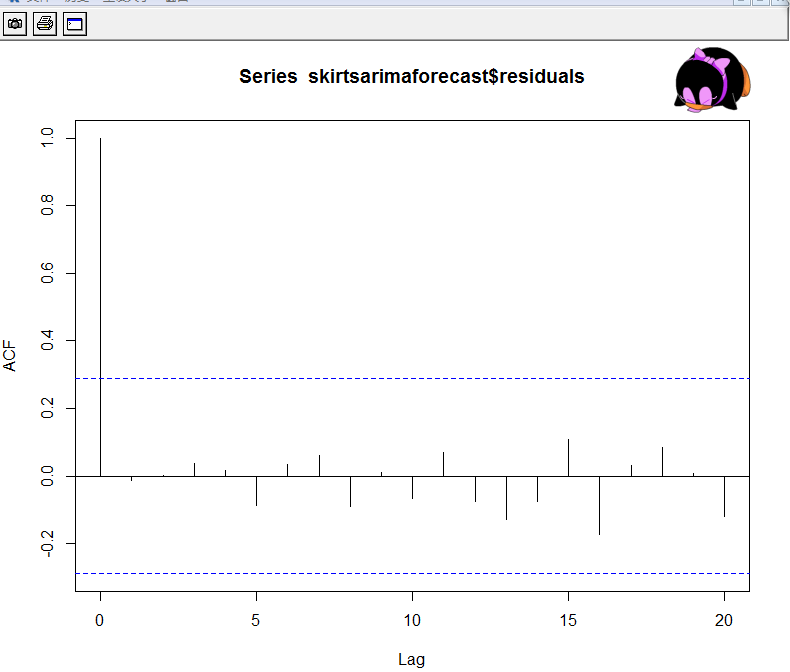
输入下面指令：

> Box.test(skirtsarimaforecast$residuals, lag=20, type="Ljung-Box")

R控制台输出：

　　   Box-Ljung test

data: skirtsarimaforecast$residuals
X-squared = 8.5974, df = 20, p-value = 0.9871

既然相 关图显示出在滞后1 - 20阶（ lags 1 - 20 ）中样本自相关值都没有超出显著（置信）边界，而且Ljung-Box检验的p值为0.99，所以我们推断在滞后1-20阶（lags1-20）中没明显证据说明预测 误差是非零自相关的。

为了调查预测误差是否是平均值为零且方差为常数的正态分布（服从零均值、方差不变的正态分布），我们可以做预测误差的时间曲线图和直方图（具有正态分布曲线）：

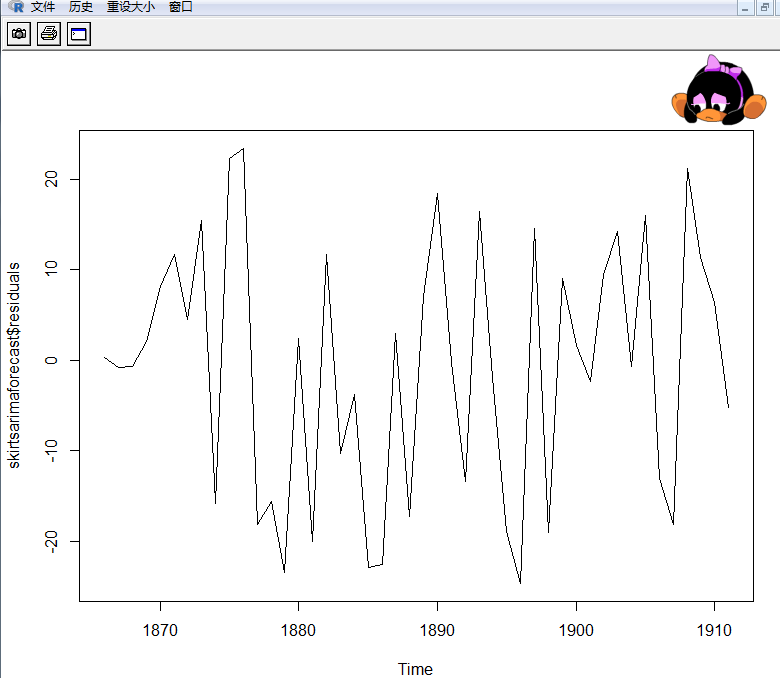
> plot.ts(skirtsarimaforecast$residuals)

下面我参考了这里http://blog.csdn.net/howardge/article/details/42002733，不过还是没成功

为了更具体的展现，我们需要借助少量的代码，首先构建函数plotForecastErrors：（我自己也没弄懂）

plotForecastErrors <- function(forecasterrors)
{
    # make a red histogram of the forecast errors:
    mysd <- sd(forecasterrors)
    hist(forecasterrors, col="red", freq=FALSE)   

    # freq=FALSE ensures the area under the histogram =
    # generate normally distributed data with mean  and standard deviation mysd
    mynorm <- rnorm(, mean=, sd=mysd)
    myhist <- hist(mynorm, plot=FALSE)   

    # plot the normal curve as a blue line on top of the histogram of forecast errors:
    points(myhist$mids, myhist$density, type="l", col="blue", lwd=)
}  

继续输入：

>source("plotForecastErrors.R")    #这里没成功

> plotForecastErrors(skirtsarimaforecast$residuals)   #显示不存在前面的函数，没解决呢

上图预测中的时间曲线图显示出对着时间增加，方差大致为常数（大致不变）（尽管上半部分的时间序

列方差看起来稍微高一些）。时间序列的直方图显示预测误大致是正态分布的且平均值接近于 0（服从零均值的正态分布的）。因此，把预测误差看作平均值为0方差为常数正态分布（服从零均值、方差不变的正态分布）是合理的。

既然依次连续的预测误差看起来不是相关，而且看起来是平均值为 0 方差为常数的正态分布（服从零均值、方差不变的正态分布），那么对于裙子直径的数据， ARIMA(1,2,5)看起来是可以提供非常合适预测的模型。

注：如果在R界面输入画图指令，但是找不到图形，可以从R控制台的”窗口”选项选择“R Graphics”，既可以调出所画图形。