三维网格去噪算法（two-step framework）

　　基于两步法的网格去噪算法顾名思义包含两个步骤：首先对网格表面的法向进行滤波，得到调整后的网格法向信息，然后根据调整后的法向更新顶点坐标位置，下面介绍三篇该类型的文章。

　　[Sun et al. 2007]文章首先介绍了当前法向滤波方法以及顶点坐标更新方法，然后提出自己的法向滤波方法和顶点坐标更新方法。

　　法向滤波方法：

　　1.均值滤波（mean filter）：n_i^’ = normalize(Σ_j∈N(i) A_j·n_j / Σ_j∈N(i) A_j)，均值滤波会破坏网格的细节特征。

　　2.中值滤波（median filter）：n_i^’ = arg median_nj {w_j⊙∠(n_i, n_j) : j∈N(i)}，中值滤波能够保持网格的细节特征，但当网格噪声较大时，效果并不好。

　　3.α-截尾滤波（alpha-trimming filter）：n_i^’ = normalize(Σ_j∈N(i) I_α(j) ·A_j·n_j)，∠(n_i, n_j)角度值前α比例和后α比例对应的I_α(j)为0，当α = 0时等同于均值滤波，当α = 0.5时等同于中值滤波。

　　4.模糊矢量中值滤波（fuzzy vector median filter）：先使用矢量中值滤波n_m = arg min_nj {Σ_k∈N(i) d(n_j, n_k) : j∈N(i)}，其中d(n_j, n_k)为n_j和n_k的L_p范数或∠(n_j, n_k)角度值，然后再使用高斯滤波n_i^’ = normalize(Σ_j∈N(i) n_j·exp(-d(n_j, n_m)²/2σ²))。模糊矢量中值滤波可以得到误差较小的法向，但会增加计算量。

　　5.[Sun et al. 2007]文章法向滤波方法：n_i^’ = normalize(Σ_j∈N(i) h_j·n_j)，权重定义为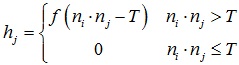，其中N(i)为三角片f_i的邻域三角片集，有两种选择，见下图，f(x) = x²，0 ≤ T ≤ 1，T的取值决定了邻域三角片N(i)中有多少三角片法向会参与计算，当T = 1时，只有与n_i相等的邻域三角片法向会参与计算，而当T = 0时，所有邻域三角片法向都会参与计算。当网格有明显棱边时，T可以取相对较小值，而当网格比较光滑时，T可以取相对较大值。

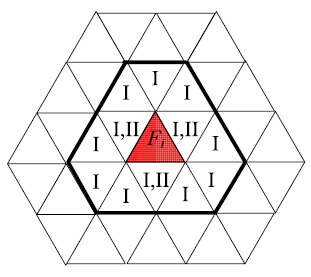
Ⅰ基于顶点（vertex based）的三角片邻域；Ⅱ表示基于边（edge based）的三角片邻域

　　顶点坐标更新方法：

　　1.求解线性方程组：

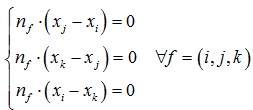
　　2.梯度下降法：

其中N_v(i)为顶点i的1环邻域顶点集。

　　3. [Sun et al. 2007]文章顶点更新方法：

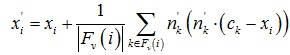
其中F_v(i)为顶点i的1环邻域三角片集。

效果：

　　[Zheng et al. 2011]文章提出了两种三角片法向更新方法，而其顶点坐标更新方法采用和[Sun et al. 2007]文章一样的方法。

　　1.Local and Iterative Scheme：

　　该方法采用对法向进行双边滤波：n_i^t+1 = K_i·Σ_j∈N(i) w_ij·n_j^t，其中N(i)为三角片f_i的邻域三角片集，K_i为归一化系数，w_ij = ξ_ij·W_c·W_s，ξ_ij为三角片f_j的面积S_i，空间域核W_c(||c_i – c_j||) = exp(-||c_i – c_j||²/2σ_c²)，值域核W_s(||n_i – n_j||) = exp(-||n_i – n_j||²/2σ_s²)。

　　2. Global and Non-Iterative Scheme：

　　该方法通过求解线性方程组来最小化目标函数，相对于上面的显式更新顶点坐标方法，该方法是一种对应的隐式更新顶点坐标方法，目标函数如下：

其中A_i = S_i/mean({S})，上式等同于求解线性方程组，但是方程不满秩，需要加入软约束条件：E_d = Σ_i A_i·||n_i^’ – n_i||²。最后优化目标为：argmin(1 - λ) ·E_s + λ·E_d，其中λ∈[0, 1]，用于控制网格的光滑程度。

效果：

 

　　[Zhang et al. 2015]文章提出了一种三角片法向更新方法，该方法与[Zheng et al. 2011]文章的方法一相似，不同的是[Zheng et al. 2011]文章采用原始法向作为双边滤波中的值域信息，而[Zhang et al. 2015]文章对原始法向进行引导滤波（guided filter）得到新的法向作为值域信息。而其顶点坐标更新方法同样采用和[Sun et al. 2007]文章一样的方法。

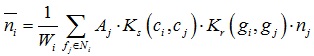
其中N_i为三角片f_i的邻域三角片集，W_i为归一化系数，A_j为三角片f_j的面积，空间域核K_s和值域核K_r都为高斯核函数。

　　关键如何计算三角片f_i的引导法向（guidance）g_i，文章提出对于三角片f_i，在其周围寻找一个包含三角片f_i的区域，使该区域内的三角片法向变化最小，然后将这个区域里的所有三角片法向进行加权平均作为三角片f_i的引导法向。具体来说，定义P_k为与三角片f_i拥有共同顶点的三角片集{f_k}，那么三角片f_i的候选区域（candidate patch）为C(f_i) = {P_k∣f_i∈P_k}。对于每个区域P∈C(f_i)，计算区域P内三角片法向的一致性（consistency）：H(P) = Ф(P)·R(P)，其中Ф(P)为区域P内三角片法向的最大偏差：Ф(P) = max_fj,fk∈P ||n_j – n_k||，R(P)为区域P内相邻三角片法向的相对变化程度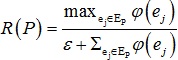：，式中φ(e_j) = ||n_j1 – n_j2||。然后选取其中一致性函数H(P)最小的区域P^*，并对其中的三角片法向作面积加权平均，即得到三角片f_i的引导法向g_i：g_i = normalize(Σ_fj∈P* A_j·n_j)。

效果：

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。

参考文献：

[1] Xianfang Sun; Rosin, P.L.; Martin, R.R.; Langbein, F.C., "Fast and Effective Feature-Preserving Mesh Denoising," Visualization and Computer Graphics, IEEE Transactions, vol.13, no.5, pp.925-938, Sept.-Oct. 2007.

[2] Youyi Zheng; Hongbo Fu; Au, O.K.-C.; Chiew-Lan Tai, "Bilateral Normal Filtering for Mesh Denoising," Visualization and Computer Graphics, IEEE Transactions, vol.17, no.10, pp.1521-1530, Oct. 2011.

[3] Wangyu Zhang, Bailin Deng, Juyong Zhang, Sofien Bouaziz, Ligang Liu, "Guided Mesh Normal Filtering," Computer Graphics Forum (Proc. Pacific Graphics), 34(7): 23–34, 2015.