c++求最小公倍数和最小公约数

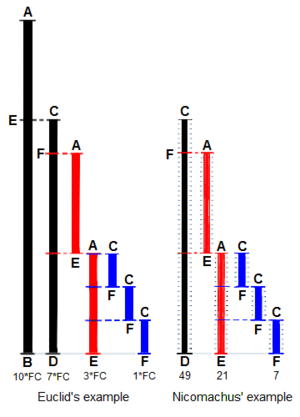
方法一：辗转相除法(欧几里得 Euclidean）

　　用“较大数”除以“较小数”，再用较小数除以第一余数，再用第一余数除以第二余数；

反复直到余数为零为止。

#include<iostream>
#include<algorithm>
using namespace std;

/*其计算原理依赖于下面的定理：

定理：gcd(a,b) = gcd(b,a mod b)

证明：a可以表示成a = kb + r，则r = a mod b 
假设d是a,b的一个公约数，则有 
d|a, d|b，而r = a - kb，因此d|r 
因此d是(b,a mod b)的公约数

假设d 是(b,a mod b)的公约数，则 
d | b , d |r ，但是a = kb +r 
因此d也是(a,b)的公约数

因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证
using namespace std;
*/

int gcd(int a,int b)
{
    if(b == )
        return a;
    return gcd(b,a%b);
}

int main()
{
    int a, b;

    cin>>a>>b;
    int c = gcd(a,b);
    printf("%d",c);
}