P1983 车站分级

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级别，最低为 1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

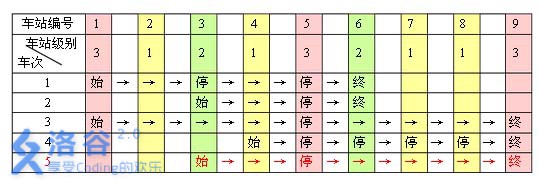
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

输入输出格式

输入格式：

输入文件为 level.in。

第一行包含 2 个正整数 n, m，用一个空格隔开。

第 i + 1 行（1 ≤ i ≤ m）中，首先是一个正整数 si（2 ≤ si ≤ n），表示第 i 趟车次有 si 个停靠站；接下来有 si个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：

输出文件为 level.out。

输出只有一行，包含一个正整数，即 n 个火车站最少划分的级别数。

输入输出样例

输入样例#1： 复制

9 2
4 1 3 5 6
3 3 5 6 

输出样例#1： 复制

2

输入样例#2： 复制

9 3
4 1 3 5 6
3 3 5 6
3 1 5 9 

输出样例#2： 复制

3

说明

对于 20%的数据，1 ≤ n, m ≤ 10；

对于 50%的数据，1 ≤ n, m ≤ 100；

对于 100%的数据，1 ≤ n, m ≤ 1000。

拓扑排序

没停靠的点一定比停靠点等级小

这两类点连边就行

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define inf 2147483647
const ll INF = 0x3f3f3f3f3f3f3f3fll;
#define ri register int
template <class T> inline T min(T a, T b, T c)
{
    return min(min(a, b), c);
}
template <class T> inline T max(T a, T b, T c)
{
    return max(max(a, b), c);
}
template <class T> inline T min(T a, T b, T c, T d)
{
    return min(min(a, b), min(c, d));
}
template <class T> inline T max(T a, T b, T c, T d)
{
    return max(max(a, b), max(c, d));
}
#define scanf1(x) scanf("%d", &x)
#define scanf2(x, y) scanf("%d%d", &x, &y)
#define scanf3(x, y, z) scanf("%d%d%d", &x, &y, &z)
#define scanf4(x, y, z, X) scanf("%d%d%d%d", &x, &y, &z, &X)
#define pi acos(-1)
#define me(x, y) memset(x, y, sizeof(x));
#define For(i, a, b) for (int i = a; i <= b; i++)
#define FFor(i, a, b) for (int i = a; i >= b; i--)
#define bug printf("***********\n");
#define mp make_pair
#define pb push_back
const int N = ;
const int M=;
// name*******************************
int n,m;
int vis[N];
int d[N][N];
int in[N];
struct edge
{
    int to,next;
} e[M];
int Head[N];
int a[N];
int tot=;
queue<int>que;
int ans=;
// function******************************
void add(int u,int v)
{
    e[++tot].to=v;
    e[tot].next=Head[u];
    Head[u]=tot;
}
int topo()
{
    me(a,);
    For(i,,n)
    if(in[i]==)
        que.push(i);
    while(!que.empty())
    {
        int u=que.front();
        que.pop();
        for(int p=Head[u]; p; p=e[p].next)
        {
            int v=e[p].to;
            in[v]--;
            if(in[v]==)
            {
                a[v]=a[u]+;
                que.push(v);
                ans=max(a[v]+,ans);
            }
        }
    }
    return ans;
}

//***************************************
int main()
{
//    ios::sync_with_stdio(0);
//    cin.tie(0);
//    freopen("test.txt", "r", stdin);
    //  freopen("outout.txt","w",stdout);
    cin>>n>>m;
    while(m--)
    {
        me(a,);
        me(vis,);
        int t;
        scanf("%d",&t);
        For(i,,t)
        {
            scanf("%d",&a[i]);
            vis[a[i]]=;
        }
        For(i,a[]+,a[t])
        if(!vis[i])
            For(j,,t)
            if(!d[i][a[j]])
            {
                d[i][a[j]]=;
                in[a[j]]++;
                add(i,a[j]);
            }
    }

    cout<<topo();

    return ;
}