LGV引理

LGV引理是用来统计DAG中固定若干起点和终点情况下的选择不相交链的方案数的。

同样用来优化计数问题，但是比Pólya定理友好多了，这也就是为什么它能够被直接糊到NOI考场上。

对于一张DAG，每条边有一个边权 \(\omega(e)\) ，我们记一条路径 \(P\) 的权值 \(\omega(P)=\prod\limits_{e\in P}\omega(e)\) ，我们再记点 \(u\) 到点 \(v\) 的所有路径的权值之和为 \(e(u,v)\) 。

设我们有一个起点集合 \(A={a_1,a_2\dots a_k}\) 和一个终点集合 \(B={b_1,b_2\dots b_k}\) ，满足 \(|A|=|B|\) ，我们设 \(P\) 为它的一个选择不相交链的方案，我们同时记 \(t(P)\) 表示将终点按对应起点下标对应得到的排列的逆序对数 。

铺垫了这么多，终于到了LGV引理的主题部分：

对于行列式 \(M=\begin{vmatrix}e(a_1,b_1)&e(a_1,b_2)&\dots&e(a_1,b_k)\\e(a_2,b_1)&e(a_2,b_2)&\dots&e(a_2,b_k)\\\vdots&\vdots&\ddots&\vdots\\e(a_k,b_1)&e(a_k,b_2)&\dots&e(a_k,b_k)\\\end{vmatrix}\) ，我们有 \(\det M=\sum\limits_{P}(-1)^{t(P)}\prod\limits_{P_i\in P}\omega(P_i)\) 。

也就是，我们可以通过求出行列式 \(M\) 的值，来统计不相交链的方案数。

这里给出一个感性的证明：

首先， \(M\) 必然是统计了所有选择 \(k\) 条链的方案（无论是否有相交），假设我们找到其中一种有相交的方案，找到它的一个相交的节点以及在这个点相交的两条链（我们假定已经将所有的节点和链按照一定顺序排序以保证一一对应）：



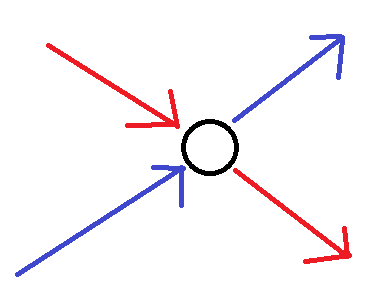
假设我们将这两条链在这个点之后路径交换：



不难发现，这两种情况下的 \(\prod\limits_{P_i\in P}\omega(P_i)\) 是一样的，但 \(t(P)\) 因为交换了排列中的两个数的位置，奇偶性改变。

所以在 \(\det M\) 中，这两项刚好抵消，所以只会剩下不相交的了，也就是右式。

当所有的边权都取 \(1\) 的时候，就是对不相交链方案数的统计了。

例题时间：

P6657 【模板】LGV 引理

发现不相交链选择的情况只有 \(a_i\) 与 \(b_i\) 对应的情况，所以 \(\det M\) 即为答案。

考虑从 \(a_i\) 到 \(b_j\) 有多少种方案：\(e(a_i,b_j)=\begin{cases}\dbinom{n+b_j-a_i}{b_j-a_i}&b_j\geqslant a_i\\0&b_j<a_i\end{cases}\) 。

处理出来即可，最终复杂度为 \(O(n+m^3)\) 。

[NOI2021] 路径交点

考虑当交点数为 \(k\) 的时候， \(P\) 对应排列相对于排列 \(1,2\dots n_1\) 相当于进行了 \(k\) 次相邻两两交换，对答案的贡献和引理中一样，均为 \((-1)^k\) ，用DP维护从每个起点到每个终点的方案数，然后对行列式求值即可，最终复杂度为 \(O(\sum m+n^3)\leqslant O(n^3)\) 。

CF348D Turtles

两只乌龟路径分别为 \((1,2)\rightarrow(n-1,m)\) 和 \((2,1)\rightarrow(n,m-1)\) ，只有符合答案的情况能够做到两两不相交，设 \(S(x_1,y_1,x_2,y_2)\) 为 \((x_1,y_1)\rightarrow(x_2,y_2)\) 的方案数，答案就是 \(\begin{vmatrix}S(1,2,n-1,m)&S(1,2,n,m-1)\\S(2,1,n-1,m)&S(2,1,n,m-1)\end{vmatrix}=S(1,2,n-1,m)S(2,1,n,m-1)-S(1,2,n,m-1)S(2,1,n-1,m)\) ，DP出答案式中的四个值即可，最终复杂度为 \(O(nm)\) 。

[PA2021] Fiolki 2

发现我们需要判断的是一个类似于去 \(k\) 条不相交的链的东西，所以考虑使用 LGV 引理。

因为只需判断是否合法，但是 LGV 是在进行带符号求和，所以考虑对每一条边随机赋一个边权，有解的可以近似等价于行列式的值不为零。

我们记 \(ed_{u,v}\) 表示 DAG 上 \(u\) 到 \(v\) 所有路径上边权积的和（也就是 LGV 要的那个东西）。

但是不一定能够取满 \(k\) 个，记 \(1\dots k\) 号节点到某一个点 \(u,u=k+1\dots n\) 的 \(ed\) 值为一个 \(k\) 维向量 \(\alpha_u=(ed_{1,u},ed_{2,u}\dots ed_{k,u})\) 。

不难发现，\(f(l,r)\) 的值就等价于 \(\alpha_l,\alpha_{l+1}\dots \alpha_r\) 构成的线性基的大小。

考虑使用时间戳线性基维护即可。