【图论】Floyd消圈算法

毫无卵用的百度百科

Definition&Solution

　　对于一个给定的链表，如何判定它是否存在环以及环的长度问题，可以使用Floyd消圈算法求出。

　　从某种意义上来讲，带环的链表在本质上是一个有向图

　　考虑下面的事实：假定小Y和小Z在圆形操场上跑步，小Z的速度是小Y的两倍，那么总存在一个时刻，使得小Z和小Y在同一个位置但是小Z比小Y多跑了若干圈。

　　该算法的复杂度为O(n)。

　　代码如下：

void floyd_c() {
    int c1=list_begin,c2=list_begin;//c=child
    do {
        c1=nxt[c1];
        c2=nxt[c2];    dosth();
        c2=nxt[c2];    dosth();
    } while(c1!=c2);
    return;
}

　　其中dosth应具体情况具体分析。

　　考虑如何求出该环的起点。

　　如果你不理解环为什么有起点，不妨观察下面的链表：

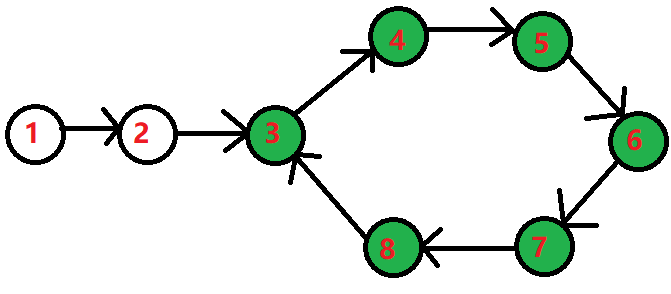
　　由于1是链表的起点，以1号点为起点遍历整张链表，是从3号点进入原谅环的，我们认为3号点是原谅环的起点。

　　如何求出起点。

　　将小Z和小Y都放到链表的起点上，当两者相遇时，将其中一个指针再次放到起点上，二者再次相遇的位置就是环的起点。

　　证明如下：

　　　　由于含有多个环的链表可以通过数学归纳由含有一个环的链表证明，故不妨设所研究的链表只有一个环，同时还有一条长度至少为1（一个点）的链。

　　　　设环的长度为n，链的长度为m。快慢指针第一次相遇在环上的第k个点，那么有：

　　　　快指针的路程Sa=m+A*n+k，其中A∈Z，代表走了几圈①

　　　　慢指针的路程Sb=m+B*n+k。其中B∈Z，代表走了几圈②

　　　　由于快指针的速度是慢指针的两倍，即：

　　　　Va=2Vb③

　　　　在运动时间一定的情况下有：

　　　　Sa=2Sb④

　　　　①-②得：

　　　　Sa-Sb=(A-B)*n⑤

　　　　联立④⑤解得Sb=(A-B)*n⑥

　　　　由于A，B∈Z，且显然A>B，所以Sa，Sb都是圈长度的倍数。

　　　　不妨设Sb=T*n。显然从起点出发，走过T*n+m时，到达环的起点。

　　　　那么在两个指针相遇时，我们让两个指针的速度都为1，走m个单位就可以到达环的起点，这时快指针的路程为2Sb+m。慢指针的路程为Sb+m。

　　　　由于Sb=T*n，这时的路程可以理解为快指针走到m处然后绕了几圈，绕圈路程为2Sb，慢指针从路程为Sb的位置走了m，那么二者的相遇的地方显然是环的起点。

　　　　特别的，因为vb=1。所以Sb即为循环的次数。通过⑥式已经证明，该算法的复杂度为O(n)。其中常数随环的形态而改变。

 

Sample

UVA11549 Calculator Conundrum

Description

有一个非常无聊的傻逼，有一天他闲的没事干玩一个老式计算器，这个计算器只能显示答案最高的n位。比如n=2，计算99+1的答案为100时，显示为10。

现在他一开始输入了一个数字k，保证在能显示的范围内，然后将k平方，然后将答案平方，再平方……

这个无聊的人想知道屏幕上显示的最大数时多少。

Input

第一行是数据组数，对于每组数据，包含：

• 一个整数n，一个整数k

Output

对于每组数据，输出：

• 对应答案

Sample Input

Sample Output

Hint

n≤9

Solution

简单的数学归纳可以证明计算器上的数字是会出现循环的,可以使用Floyd消圈算法解决此题。

Code

#include<cstdio>
#define rg register
#define ci const int
#define ll long long int

inline void qr(int &x) {
    char ch=getchar(),lst=NULL;
    while(ch>''||ch<'') lst=ch,ch=getchar();
    while(ch>=''&&ch<='') x=(x<<)+(x<<)+(ch^),ch=getchar();
    if (lst=='-') x=-x;
}

char buf[];
inline void write(int x,const char aft,const bool pt) {
    if(x<) {putchar('-');x=-x;}
    int top=;
    do {
        buf[++top]=x%+'';
        x/=;
    } while(x);
    while(top) putchar(buf[top--]);
    if(pt) putchar(aft);
}

template <typename T>
inline T mmax(const T &a,const T &b) {if(a>b) return a;return b;}
template <typename T>
inline T mmin(const T &a,const T &b) {if(a<b) return a;return b;}
template <typename T>
inline T mabs(const T &a) {if(a<) return -a;return a;}

template <typename T>
inline void mswap(T &a,T &b) {T temp=a;a=b;b=temp;}

int t,n,k,ans;

int nxt(ci);

int main() {
    qr(t);
    while(t--) {
        n=k=;qr(n);qr(k);
        int c1=k,c2=k;ans=k;
        do {
            c1=nxt(c1);
            c2=nxt(c2);ans=mmax(ans,c2);c2=nxt(c2);ans=mmax(ans,c2);
        } while(c1!=c2);
        write(ans,'\n',true);
    }
    return ;
}

short bufff[];
int nxt(int x)
{
    if(!x)return ;
    long long kf=(long long)x*x;
    int L=;
    while(kf>) bufff[L++]=kf%,kf/=;
    int temp=n;
    if(temp>L) temp=L;
    int sum=;
    for(int i=;i<temp;++i) sum=(sum<<)+(sum<<)+bufff[--L];
    return sum;
}

Summary

　　1、Floyd消圈算法是达到理论下限的判断有向图上环的算法。尽管它的常数难以控制，但是十分的实用并且好写。

　　2、在证明的最后使用了等效替代法，在其他的OI毒瘤题中，也应注意该方法的应用。