LCA--倍增法

一般来求LCA有3种方法

1.倍增

2.RMQ+欧拉序

3.tarjan（离线）

本文将倍增求lca

这个算法是很常见很常见的

也是较好理解的

（我也不明白假期学长讲的时候我为什么死活都不明白

　自闭qwq

　对不起学长qwq

　明明学长讲的是最好的qwq

　想学长了qwq）

---------------------------------------------------------------------------

一、基础概念

LCA定义：

　　LCA（Lowest Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。

如图，结点4，6的公共祖先有1、2，但最近的公共祖先是2，即Lca(4,6) = 2

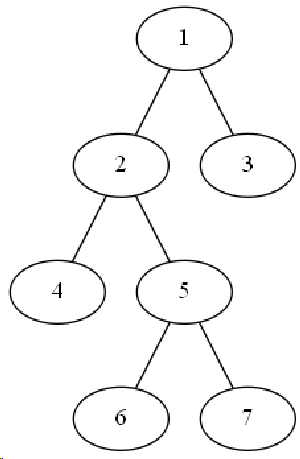
显然遇到这个问题

首先会想到暴力

再一算

时间复杂度"仅仅"是O(n)而已啦

可是如果有q次询问呢

比如说洛谷板子题

n和q（这里的q即板子题中的m都是5 * 10⁵的级别的

那么n*q就是一个不小的数了

那么暴力一定是过不了的了

那么就只能优化优化了

--------------------------------------------------------------------

倍增法：

注意到u，v走到最近公共祖先w之前，u，v所在结点不相同。

而到达最近公共祖先w后，再往上走仍是u，v的公共祖先，即u，v走到同一个结点，这具有二分性质。

于是可以预处理出一个2k的表，

fa[k][u]表示u往上走2k步走到的结点，令根结点深度为0，则2k>depth[u]时，令fa[k][u]=-1(不合法情况的处理）

不妨假设depth[u] < depth[v]

①将v往上走d = depth[v] - depth[u]步，此时u，v所在结点深度相同，该过程可用二进制优化。

由于d是确定值，将d看成2的次方的和值，d = 2k1 + 2k2 + ... + 2km，利用fa数组，如v = fa[k1][v]，v = fa[k2][v]加速。

②若此时u = v，说明Lca(u,v)已找到

③利用fa数组加速u，v一起往上走到最近公共祖先w的过程。

令d = depth[u] - depth[w]，虽然d是个未知值，但依然可以看成2的次方的和。

从高位到低位枚举d的二进制位，设最低位为第0位，若枚举到第k位，有fa[k][u] != fa[k][v]，则令u = fa[k][u]，v = fa[k][v]。

最后

最近公共祖先w = fa[0][u] = fa[0][v]，即u和v的父亲

　

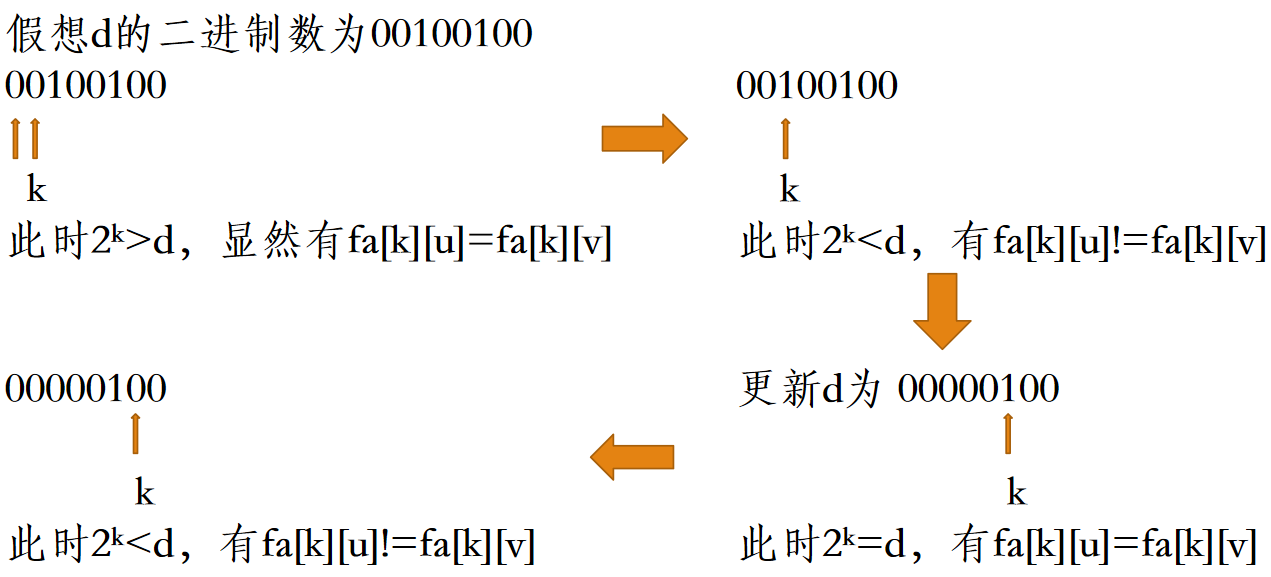
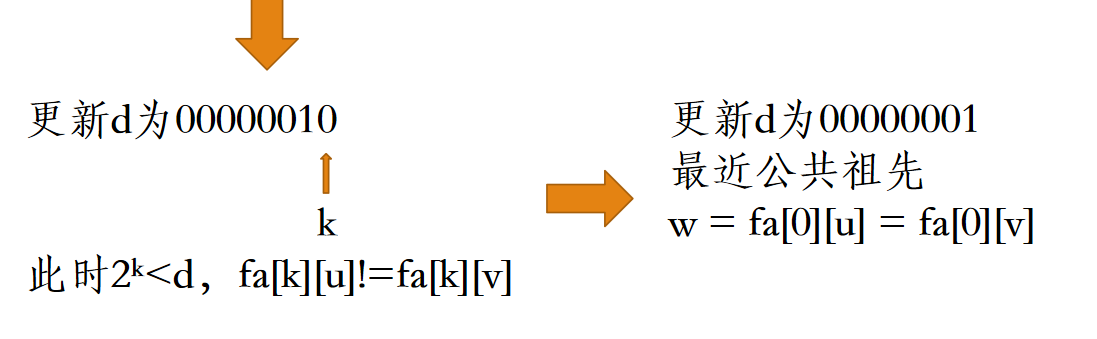
如何预处理？
    k=0时，fa[k][u]为u在有根树中的父亲，令根结点fa[k][root]=-1。

　k>0时，fa[k][u]=fa[k-1][fa[k-1][u]]。树的高度最多为n，k是logn级别。

时间复杂度？
    预处理O(nlogn)
    单次查询O(logn)

来个板子题也很好理解呀（传送门）

上面提到过的

罗姑上也有板子题

但是我最近是由hdu的oj写的

正好还有那个的代码就直接拿过来了

#include<cstdio>
#include<iostream>
#include<cstring>
#define maxn 40000
using namespace std;

struct EDGE
{
    int nxt,to,v;
}edge[maxn*+];
//链式前向星（可以用结构体，也可以用独立的数组）
//注意这里结构体的大小，下面会说的 

int T,n,root,cnt,m;
//T次模拟，cnt为边的个数（边的编号），n个点的树，m次询问，root是树的根（有的lca中没有给出根节点的标号，需要自己找，这里就没给）
int head[maxn+],dep[maxn+],dis[maxn+];
//head也是属于链前中的内容，写在这里因为[]中为点的标号，所以它的大小就是节点数的大小
//dep存每个节点的深度，dis存每个节点到根节点的深度
int f[maxn+][];//前面的[i]为i节点 ，后面的[j]为从i节点往上跳2^j个节点
bool vis[maxn+];//用来找根节点特意开的一个数组 

void add(int x,int y,int z)//加边（用链式前向星存边）
{
    edge[++cnt].to=y;
    edge[cnt].v=z;
    edge[cnt].nxt=head[x];
    head[x]=cnt;
}

void dfs(int u,int fa)
{
    dep[u]=dep[fa]+;//深度加一
    for(int i=; i<=; i++)//预处理，处理出u节点蹦2^i个节点所到达的节点编号
    {
        f[u][i+]=f[f[u][i]][i];
    }
    for(int i=head[u]; i; i=edge[i].nxt)//遍历他的出边（dfs）
    {
        if(edge[i].to==fa)
        {
            continue;
        }//（因为正反都加边了）如果这个边指向的点是u节点的父节点，不dfs这个
        dis[edge[i].to]=dis[u]+edge[i].v;//距离
        f[edge[i].to][]=u;//父节点
        dfs(edge[i].to,u);
    }
}

int LCA(int x,int y)
{
    if(dep[x]<dep[y])
    {
        swap(x,y);
    }//使x是最深的那个点
    for(int i=; i>=; i--)
    {
        if(dep[f[x][i]]>=dep[y])//如果蹦的话x的深度仍比y的深度深，那就蹦，否则不蹦
        {
            x=f[x][i];
        }
        if(x==y)//如果x蹦到了y，那么此时的x（也就是y）就是lca
        {
            return x;
        }
    }
    //此时x和y的深度相同，但不是同一个节点
    for(int i=; i>=; i--)
    {
        if(f[x][i]!=f[y][i])//如果x和y蹦完了到了相同的节点，那么蹦到的节点一定大于或等于lca
        {//所以只有蹦到了不同的节点，才可以蹦（这样才能保证没蹦超出lca）
            x=f[x][i];
            y=f[y][i];
        }
    }
    return f[x][];//离真正的lca只差一步（此时不管蹦多少都超，所以前面的循环只能使x是离lca只差一层的节点）
}

int main()
{
    scanf("%d",&T);
    while(T--)//T次模拟（每次询问都是用新的树，因此要把之前的数组全部清空）
    {
        memset(vis,,sizeof(vis));
        memset(edge,,sizeof(edge));
        memset(f,,sizeof(f));
        memset(dep,,sizeof(dep));
        memset(head,,sizeof(head));
        memset(dis,,sizeof(dis));
        cnt=;
        scanf("%d%d",&n,&m);
        for(int i=; i<=n-; i++)
        {
            int x,y,z;
            scanf("%d%d%d",&x,&y,&z);
            vis[y]=;
            add(x,y,z);
            add(y,x,z);//因为不知道x和y谁是爸爸，所以就正反都加边 ，所以结构体的大小要开两倍
        }
        for(int i=; i<=n; i++)
        {
            if(vis[i]==)
            {
                root=i;
                break;
            }
        }//没有被标记过的是根节点
        dfs(root,);
        for(int i=; i<=m; i++)
        {
            int a,b;
            scanf("%d%d",&a,&b);
            printf("%d\n",dis[a]+dis[b]-*dis[LCA(a,b)]);
        }
    }
    return ;
}