bzoj4842 Delight for a Cat

题意：n天内你每天可以s或者e，分别有一定的收益。

每连续k天中s的天数要大于ds，e的天数要大于de，求最大收益。

解：费用流解线性规划。

先假设全部选e，然后一天s的收益为si - ei

ai表示第i天是否s，up = k - de, down = ds, R = up - down，有：

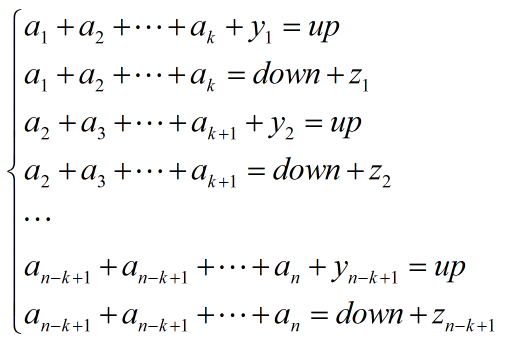
两两做差：

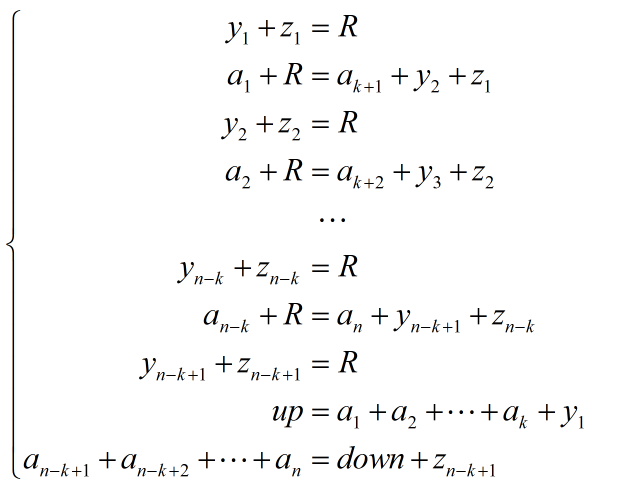
最后两个式子是人为补全的，这样就满足：每个变量在等号左边和右边各出现一次。

把每个等号看做点，每个值看做一条边。

常数项就连向源汇。

y和z代表的边啥都不需要限制，a要限流为1，费用为si - ei，然后求最大费用最大流即可。

输出方案：看改变量代表的边是否有流量即可。

 #include <cstdio>
 #include <algorithm>
 #include <queue>
 #include <cstring>

 typedef long long LL;
 const int N = , M = ;
 const LL INF = 0x3f3f3f3f3f3f3f3f;

 struct Edge {
     int nex, v;
     LL c, len;
 }edge[M << ]; int top = ;

 int e[N], vis[N], pre[N];
 LL d[N], flow[N];
 std::queue<int> Q;
 LL vs[N], ve[N];

 inline void add(int x, int y, LL z, LL w) {
     top++;
     edge[top].v = y;
     edge[top].c = z;
     edge[top].len = w;
     edge[top].nex = e[x];
     e[x] = top;

     top++;
     edge[top].v = x;
     edge[top].c = ;
     edge[top].len = -w;
     edge[top].nex = e[y];
     e[y] = top;
     return;
 }

 inline bool SPFA(int s, int t) {
     memset(d, 0x3f, sizeof(d));
     d[s] = ;
     flow[s] = INF;
     vis[s] = ;
     Q.push(s);
     while(!Q.empty()) {
         int x = Q.front();
         Q.pop();
         vis[x] = ;
         for(int i = e[x]; i; i = edge[i].nex) {
             int y = edge[i].v;
             if(edge[i].c && d[y] > d[x] + edge[i].len) {
                 d[y] = d[x] + edge[i].len;
                 pre[y] = i;
                 flow[y] = std::min(flow[x], edge[i].c);
                 if(!vis[y]) {
                     vis[y] = ;
                     Q.push(y);
                 }
             }
         }
     }
     return d[t] < INF;
 }

 inline void update(int s, int t) {
     LL temp = flow[t];
     while(t != s) {
         int i = pre[t];
         edge[i].c -= temp;
         edge[i ^ ].c += temp;
         t = edge[i ^ ].v;
     }
     return;
 }

 inline LL solve(int s, int t, LL &cost) {
     LL ans = ;
     cost = ;
     while(SPFA(s, t)) {
         ans += flow[t];
         cost += flow[t] * d[t];
         update(s, t);
     }
     return ans;
 }

 int main() {
     int n, k, ds, de;
     LL sum = ;
     scanf("%d%d%d%d", &n, &k, &ds, &de);
     for(int i = ; i <= n; i++) {
         scanf("%lld", &vs[i]);
     }
     for(int i = ; i <= n; i++) {
         scanf("%lld", &ve[i]);
         sum += ve[i];
         vs[i] -= ve[i];
     }
     int up = k - de,  down = ds, lm = n - k + ;
     int s = N - , t = N - ;
     for(int i = ; i <= n - k + ; i++) {
         if(i == ) { // yi
             add(i, lm *  + , INF, 0ll);
         }
         else {
             add(i, lm + i - , INF, 0ll);
         }
         if(i == n - k + ) { // zi
             add(i, lm *  + , INF, 0ll);
         }
         else {
             add(i, lm + i, INF, 0ll);
         }
     }
     int OP = top;
     for(int i = ; i <= n; i++) {
         // ai
         int ss = lm + i, tt = i - k + lm;
         if(i <= k) {
             tt = lm *  + ;
         }
         if(i >= n - k + ) {
             ss = lm *  + ;
         }
         add(ss, tt, 1ll, -vs[i]);
     }
     int ED = top;
     for(int i = ; i <= n - k + ; i++) {
         add(s, i, up - down, 0ll);
         add(i + lm, t, up - down, 0ll);
     }
     add(lm *  + , t, up, 0ll);
     add(s, lm *  + , down, 0ll);

     LL ans;
     solve(s, t, ans);
     printf("%lld\n", sum - ans);
     for(int i = OP + ; i <= ED; i += ) {
         if(edge[i].c) {
             putchar('E');
         }
         else {
             putchar('S');
         }
     }
     return ;
 }

AC代码