51 nod 1212 无向图最小生成树（Kruckal算法/Prime算法图解）

1212 无向图最小生成树

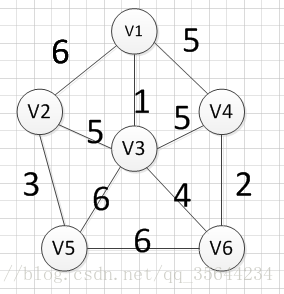
N个点M条边的无向连通图，每条边有一个权值，求该图的最小生成树。

收起

输入

第1行：2个数N,M中间用空格分隔，N为点的数量，M为边的数量。（2 <= N <= 1000, 1 <= M <= 50000)
第2 - M + 1行：每行3个数S E W，分别表示M条边的2个顶点及权值。(1 <= S, E <= N，1 <= W <= 10000)

输出

输出最小生成树的所有边的权值之和。

输入样例

9 14
1 2 4
2 3 8
3 4 7
4 5 9
5 6 10
6 7 2
7 8 1
8 9 7
2 8 11
3 9 2
7 9 6
3 6 4
4 6 14
1 8 8

输出样例

37

Prim算法是直接查找，多次寻找邻边的权重最小值，而Kruskal是需要先对权重排序后查找的，所以，Kruskal在算法效率上是比Prim快的，因为Kruskal只需一次对权重的排序就能找到最小生成树，而Prim算法需要多次对邻边排序才能找到。

（1）kruskal做法（时间复杂度：O(n*n))：

        定义每个结点的初始祖先为自己，按照边的大小将结构体排序，然后依次遍历结构体，并查集查找祖先：

        1、如果两结点的祖宗节点不一样，则将其中一个结点的祖宗作为（另一个节点的祖宗）的祖宗，对应的边即为最小生成树的边

        2、如果两结点祖宗一样，则前面已将两结点连在一棵树上，对应的边不是最小生成树的边

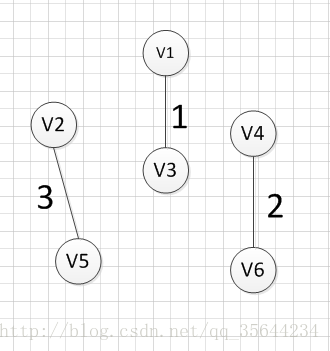
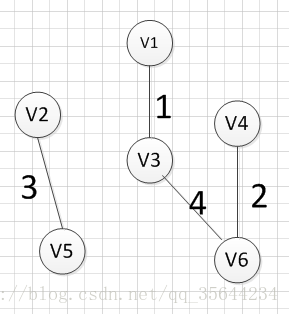
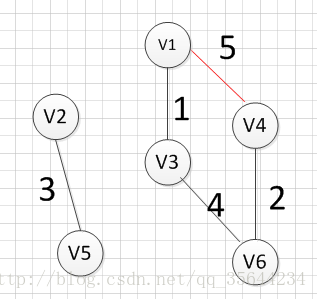
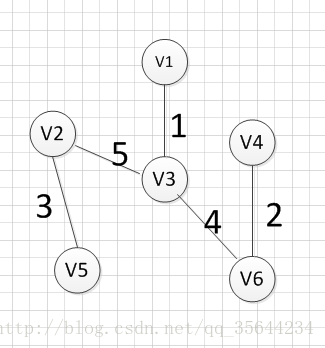
图三遍历到v3,v4连接的边，发现祖宗不同，所以将此边加入树中，图四遍历到v1,v4连接边，但是他们的祖宗（v1,v3,v4,v6中的一点）相同，所以不能加入，图五遍历到v3,v5连接的边，发现祖宗不同，所以将此边加入树中

#include<string.h>
#include<algorithm>
#define inf 9999999
using namespace std;
struct pt{
        int s,e,dis;
}a[50011];
int f[1011];
int find(int x){//并查集,寻找祖先
        return x==f[x]?f[x]:find(f[x]);
}
bool cmp(pt x,pt y){
        return x.dis<y.dis;
}
bool judge(pt p){
        int s=find(p.s);//p.s的祖先
        int e=find(p.e);//p.e的祖先
        if(s!=e){//祖先不一样说明不同一棵树上
                f[s]=e;//将两个中的一个定义为共同祖先
                return 1;
        }
        else
                return 0;
}
int main()
{
        int n,m;
        scanf("%d %d",&n,&m);
        for(int i=1;i<=n;i++)
                f[i]=i;
        for(int i=0;i<m;i++)
                scanf("%d %d %d",&a[i].s,&a[i].e,&a[i].dis);
        sort(a,a+m,cmp);
        int ans=0,cnt=0;
        for(int i=0;i<m;i++){
                if(judge(a[i])){
                        ans+=a[i].dis;
                        cnt++;
                        if(cnt==n-1)//边数达到m-1说明全部点都在树上了
                                break;
                }
        }
        printf("%d\n",ans);
        return 0;
}

（2）prime做法（时间复杂度：O(n^2))：
         对点进行操作，从起始点开始遍历找与当前点连接最近的点，每找出一个点更新一遍剩余点的拓展边（替换为最小值），各点最短拓展边的和即为结果;

#include<iostream>
#include<algorithm>
#include<string.h>
#define inf 9999999
using namespace std;
bool vis[1011];
int d[1011][1011],dis[1011];
int main()
{
        int n,m,x,y,z;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++){
                for(int j=i+1;j<=n;j++)
                        d[i][j]=d[j][i]=inf;
        }
        for(int i=0;i<m;i++){
                scanf("%d%d%d",&x,&y,&z);
                d[x][y]=d[y][x]=z;
        }
        for(int i=1;i<=n;i++)
                dis[i]=d[1][i];//初始化到i点连接边为1到i的距离
        vis[1]=1;
        int mi,id,ans=0;
        for(int k=1;k<n;k++)//遍历剩下的n个点
        {
                mi=inf;id=-1;
                for(int i=1;i<=n;i++)
                        if(!vis[i]&&mi>dis[i])
                                mi=dis[i],id=i;//找出拓展边最短的点
                vis[id]=1;
                ans+=mi;
                for(int i=1;i<=n;i++)//更新未访问点的最短拓展边
                        if(!vis[i]&&dis[i]>d[id][i])
                                dis[i]=d[id][i];
        }
        printf("%d\n",ans);
        return 0;
}